多面体理論
【英】:polyhedral theory
概要
 次元上の凸多面体とは,
次元上の凸多面体とは,  次元上の有限個の閉半空間の共通集合, すなわち
次元上の有限個の閉半空間の共通集合, すなわち 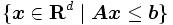 という線形不等式システムを満たすベクトルの集合である.
という線形不等式システムを満たすベクトルの集合である.  次元多面体は, 有限個の
次元多面体は, 有限個の 次元凸多面体の和集合で書き表せるものをいう. 多面体理論とは, 上で定義した多面体を, 数学的諸理論を用いて解析すること, 或いは解析された結果をいう. オペレーションズ・リサーチの分野では, 1つの凸多面体 (convex polyhedron)について論じることがほとんどである.
次元凸多面体の和集合で書き表せるものをいう. 多面体理論とは, 上で定義した多面体を, 数学的諸理論を用いて解析すること, 或いは解析された結果をいう. オペレーションズ・リサーチの分野では, 1つの凸多面体 (convex polyhedron)について論じることがほとんどである.
詳説
多面体理論 (polyhedral theory) には, 見方, 切り口によって様々な理論体系が存在する. 第一に, 古代ギリシャ時代より研究されているプラトンの正多面体, アルキメデスの準正多面体などを代表例として挙げられる古典的正多面体理論. これらの多面体は, 見た目が美しいだけでなく, 群論, 整数論, 組合せ理論など諸々の美しい数学的構造をも内包している. 詳しい内容については, 文献 [2, 1] を参照されたい.
上述の多面体理論は, 2次元或いは3次元に限定されたものである. 近年の3次元多面体に関する新たな成果として, 3次元多面体の展開図に関するものがある. 多くの読者が, 立方体 (さいころ)の展開図を厚紙に描いて切り取り, 組み立てた経験があろう. このように紙一枚に描いて切り取り, 組み立てが可能な (面どうしが重なり合わない) 図形を展開図, 英語表記では net という. 3次元正多面体には net が存在することが知られているが, 任意の3次元多面体については, 必ず net が存在するかどうかは, 未解決問題の一つである. この未解決問題に対して, 理論的, 実験的に考察を与えている文献が [7] である. 3次元多面体の辺をどのように切ったら net ができるのかを多くの種類の3次元多面体に関して考察した興味ある文献であり, また, net of polyhedron に関する参考文献リストも充実しているので, 興味ある読者は是非参照されたい.
さて, オペレーションズ・リサーチの分野において, 多大な貢献をしている多面体理論は, より一般的 (正多面体に限らないという意) かつ高次元の凸多面体 (covex polyhedron) に関するものである.
 次元ユークリッド空間の閉半空間 (closed half space) とは, 与えられた
次元ユークリッド空間の閉半空間 (closed half space) とは, 与えられた 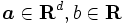 に対して
に対して

で表される集合のことである. 凸多面体 (convex polyhedron)  とは, 有限個の閉半空間の共通部分, すなわち
とは, 有限個の閉半空間の共通部分, すなわち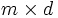 行列
行列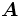 および,
および,  次元ベクトル
次元ベクトル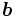 を用いて, 次のような線形不等式システムを満たすベクトルの集合として定義される.
を用いて, 次のような線形不等式システムを満たすベクトルの集合として定義される.
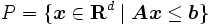
また, 凸多面体  の別の表現として, 次のものが挙げられる.
の別の表現として, 次のものが挙げられる.
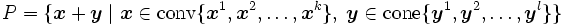
但し, 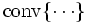 は有限個の点集合からなる凸包,
は有限個の点集合からなる凸包, 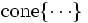 は有限個のベクトルからなる凸錘を表し, 数学的には以下のように記述される.
は有限個のベクトルからなる凸錘を表し, 数学的には以下のように記述される.
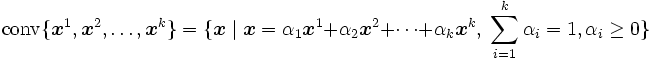
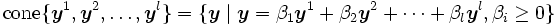
凸錘の部分が空集合であるような多面体を有界凸多面体といい, 英語では convex polytope と区別する. 重要なことは, 同じ凸多面体 を記述するのに2通りあり, 一方は可算有限個の線形不等式の共通部分と表せ, 他方は加算有限個の点の凸包内の点と可算有限個のベクトルによる凸錘内のベクトルの和として表せることである. 可算有限個という条件を除けば, 2次元平面上の円や3次元空間内の球でさえ凸多面体として定義されうることを注意しておきたい.
を記述するのに2通りあり, 一方は可算有限個の線形不等式の共通部分と表せ, 他方は加算有限個の点の凸包内の点と可算有限個のベクトルによる凸錘内のベクトルの和として表せることである. 可算有限個という条件を除けば, 2次元平面上の円や3次元空間内の球でさえ凸多面体として定義されうることを注意しておきたい.
上述のように定義された一般の凸多面体の構造は, 記述が単純でありながら解析が非常に困難であるため, 特殊な凸多面体である整数多面体や, 凸多面体を特徴付ける全ユニモジュラ性, 全双対整数性 (TDI性) 等の性質が研究されており, 整数計画, 組合せ最適化問題の解法等に大きく貢献している [8].
 を
を 次元凸多面体,
次元凸多面体, 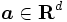 ,
, 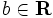 とする. 任意の
とする. 任意の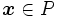 に対して,
に対して, 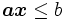 が成り立つとき,
が成り立つとき, 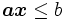 を凸多面体
を凸多面体 の妥当不等式 (valid inequality) という. 凸多面体
の妥当不等式 (valid inequality) という. 凸多面体 の部分集合
の部分集合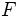 が
が のフェイス (face) であるとは, 妥当不等式
のフェイス (face) であるとは, 妥当不等式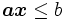 が存在し,
が存在し,
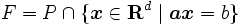
が成り立つことである. 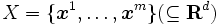 を
を 次元空間の
次元空間の 個の点集合としたとき,
個の点集合としたとき,  がアフィン独立 (affinely independent) であるとは,
がアフィン独立 (affinely independent) であるとは,
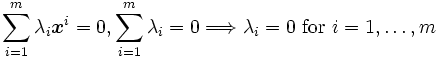
が成り立つことである. このようにアフィン独立性を定義すると, 多面体のフェイス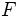 の次元
の次元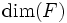 が次のように定義できる.
が次のように定義できる.
次元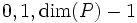 のフェイスをそれぞれ頂点 (vertex) 或いは端点 (extreme point), 辺 (edge), ファセット (facet) とよぶ. 凸多面体
のフェイスをそれぞれ頂点 (vertex) 或いは端点 (extreme point), 辺 (edge), ファセット (facet) とよぶ. 凸多面体 のファセットを構成する妥当不等式を, ファセット制約 (facet constraints) という.
のファセットを構成する妥当不等式を, ファセット制約 (facet constraints) という.
2つの端点が一つの辺を共有しているときその端点は隣接しているという. 有界な 次元凸多面体
次元凸多面体 の端点とその隣接関係を表すグラフ構造を, 多面体グラフという. 2つの端点の最短路とは, 辺の長さを1とした場合のグラフ上で最短路をいう.
の端点とその隣接関係を表すグラフ構造を, 多面体グラフという. 2つの端点の最短路とは, 辺の長さを1とした場合のグラフ上で最短路をいう.  の直径 (diameter) とは, 最短路が最も長くなるような2端点間の最短路の長さのことである. この有界凸多面体の直径に関する研究は, 端点を逐一探索していく線形計画問題における単体法の計算効率を考える意味でも重要である. 以下, 証明はされていないが凸多面体の直径
の直径 (diameter) とは, 最短路が最も長くなるような2端点間の最短路の長さのことである. この有界凸多面体の直径に関する研究は, 端点を逐一探索していく線形計画問題における単体法の計算効率を考える意味でも重要である. 以下, 証明はされていないが凸多面体の直径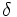 に関する有名な予想を記しておこう.
に関する有名な予想を記しておこう.
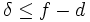
- である.
これは Hirsch の予想と呼ばれ, 一部特殊な多面体では証明されているが [5], 多面体理論における大きな未解決問題の一つである. より一般の場合に関する研究は, 文献 [4] を参照されたい.
[1] 一松信, 「正多面体を解く」, 東海大学出版会, 1983.
[2] H. S. M. Coxeter, Regular Polytopes, Dover, 1973.
[3] B. Grunbaum, Convex Polytopes}, Wiley, New York, 1967.
[4] G. Kalai, "Liner programming, the simplex algorithm and simple polytopes," Mathematical Programming, Series B, Lectures on Mathematical Programming ISMP97, T. M. Liebling and D. de Werra, eds., 79 (1997), 217-234.
[5] D. Naddef, "The Hirsch conjecture is true for (0,1)-polytopes," Mathematical Programming, 45 (1989), 109-110.
[6] W. R. Pulleyblank, "Polyhedral Combinatorics," in Optimization, G.L. Nemhauser, A.H.G. Rinnooy Kan and M.J.Todd, eds., North-Holland, 1989. 伊理正夫, 今野浩, 刀根薫監訳,『最適化ハンドブック』, 朝倉書店, 1995.
[7] W. Schlickenrieder, Nets of Polyhedra, Ph.D. thesis, Technische Universität Berlin, Germany, 1997.
[8] A. Schrijver, Theory of Linear and Integer Programming, John Wiley & Sons Ltd., 1986.
[9] J. Stoera and C. Witzgall, Convexity and Optimization in Finite Dimensions, Springer, 1970.
[10] G. M. Ziegler, Lectures on Polytopes, Springer-Verlag, New York, 1995.
- 多面体理論のページへのリンク
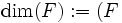 に
に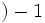
 とすると
とすると