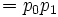多段確率決定樹表
【英】:multistage stochastic decision tree-table
概要
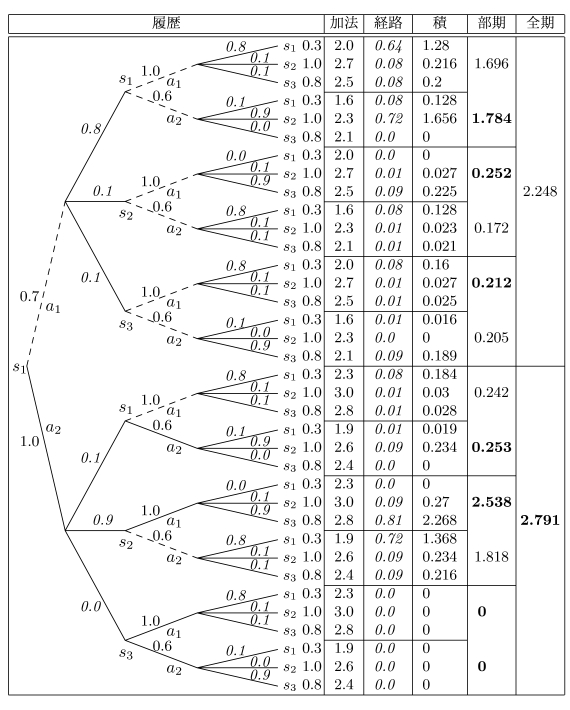
多段期待値最適化において, 問題から最適解に至るまでを1枚に図解したもの. 問題は樹(ツリー)に, 計算過程は表(テーブル)に, 最適解は樹表(ツリー・テーブル)にそれぞれ図示される. 方法としては全数列挙法(total enumeration method)であるが, 最適解の構成までが簡単明瞭に表わされている. この樹表から, 原始政策, 一般政策, マルコフ政策が生成される状況が分かる. 特に, 加法型評価に対してはマルコフ政策が最適になることが読み取れる.
詳説
多段確率決定樹表 (ツリーテーブル) は, いわゆる決定樹(ディシジョンツリー), 決定表(ディシジョンテーブル)をそれぞれ進化発展させ, 多段階にわたる確率決定過程の問題記述から最適解構成に至るまでを1枚に統合した図表である. 問題のデータを過程の進行状況に応じて配列し, あらゆる可能な経路とその評価値と確率を図示し, 各段における最適決定の選択を明示している. この意味では列挙法の解構成を与えている. この樹表ではあらゆる型の評価関数の期待値最適化, 確率最適化が解かれる. 樹表には問題に応じて繰り返し法, 直接法などいくつかの型がある[1][2][3].
ここでは3状態2決定2段(3-2-2)モデルで加法型最適化問題:
![\begin{array}{ll}
\mbox{max.} & \mbox{E}[\,r_{0}(u_{0})
+ r_{1}(u_{1}) + r_G(x_2) \,] \\
\mbox{s. t.} &
p(\,\cdot \,|x_n,u_n) \sim x_{n+1} ~\, (n = 0, 1, u_{0} \in U),
\ u_{1} \in U,
\end{array}](https://cdn.weblio.jp/e7/img/dict/orjtn/15f432c49a3eeca976cb575d7e2b29c6.png)

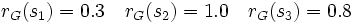

- 履歴 =
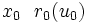 /
/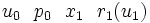 /
/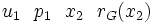
- 履歴 =
- ただし
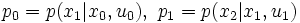
- ただし
この樹表によって 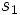 からの(最適原始決定関数を経て)最適一般決定関数
からの(最適原始決定関数を経て)最適一般決定関数
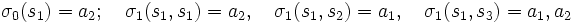
および最大値 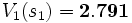 が得られる. さらに,
が得られる. さらに, 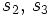 からの樹表(省略)と合わせると, マルコフ政策
からの樹表(省略)と合わせると, マルコフ政策
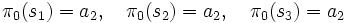
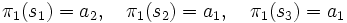
が最適になっていることがわかる. これは加法型特有の性質である. 一般に, 任意の評価関数に対しては, 原始政策, したがって一般政策が最適になる.
[1] S. Iwamoto and T. Fujita, "Stochastic Decision-making in a Fuzzy Environment," Journal of the Operations Research Society of Japan, 38 (1995), 467-482.
[2] T. Fujita and K. Tsurusaki, "Stochastic Optimization of Multiplicative Functions with Negative Value," Journal of the Operations Research Society of Japan, 41 (1998), 351-373.
[3] S. Iwamoto, K. Tsurusaki and T. Fujita, "Conditional Decision-making in a Fuzzy Environment," Journal of the Operations Research Society of Japan, 42 (1999), 198-218.
多段確率決定樹表と同じ種類の言葉
- 多段確率決定樹表のページへのリンク
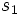 からの
からの