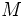凸多面体
【英】:convex polyhedron, convex polytope
概要
有限個の閉半空間の共通部分を凸多面体と呼ぶ. すなわち, 次元実線形空間
次元実線形空間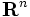 内の凸多面体
内の凸多面体 は, 適当な
は, 適当な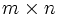 実行列
実行列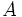 と
と 次元ベクトル
次元ベクトル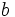 を用いて
を用いて
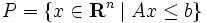
と表現できる. 特に有界な凸多面体は, convex polytope と英語では区別して呼ばれ, 有限個の点からなる集合の凸包であり, 逆も成り立つ.
詳説
 次元実ベクトル
次元実ベクトル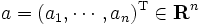 と実数
と実数 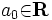 により定まる1次不等式 (線形不等式)
により定まる1次不等式 (線形不等式) 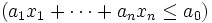 を満たす点
を満たす点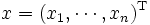 全体からなる集合を閉半空間(closed halfspace)とよぶ. 有限個の閉半空間の共通部分を凸多面体 (convex polyhedron) とよぶ. すなわち,
全体からなる集合を閉半空間(closed halfspace)とよぶ. 有限個の閉半空間の共通部分を凸多面体 (convex polyhedron) とよぶ. すなわち, 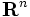 内の凸多面体は, 適当な
内の凸多面体は, 適当な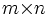 実行列
実行列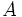 と
と 次元ベクトル
次元ベクトル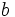 を用いて
を用いて
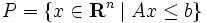
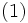
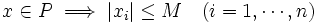
をみたすとき有界である(bounded)とよばれ, 英語では convex polytopeと区別してよばれることが多い. 凸多面体の例としては, 線形計画問題での実行可能多面体, TSP多面体, マトロイドの基多面体, ポリマトロイドなどがある.
凸多面体には不等式表現以外にもう一つ有益な表現方法がある. 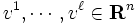 に対して, 適当な
に対して, 適当な によって
によって
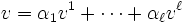
と表現されるベクトル  を
を の一次結合(線形結合) (linear combination) とよぶ. 係数
の一次結合(線形結合) (linear combination) とよぶ. 係数 が非負条件
が非負条件
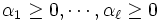
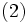
をみたす場合には  は非負結合(nonnegative combination), 和が1という条件
は非負結合(nonnegative combination), 和が1という条件
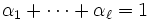
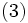
をみたす場合には  はアフィン結合 (affine combination), さらに (2) と (3) の両方をみたすとき
はアフィン結合 (affine combination), さらに (2) と (3) の両方をみたすとき  は
は の凸結合 (convex combination) とよばれる. 有限個の
の凸結合 (convex combination) とよばれる. 有限個の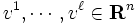 と
と に対して,
に対して,  の凸結合と
の凸結合と の非負結合の和として表される点全体, すなわち
の非負結合の和として表される点全体, すなわち
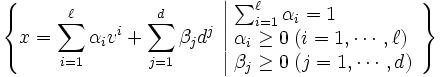
と定義される集合は凸多面体となり, 逆に (1) で定義される凸多面体については (4) をみたす有限個の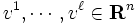 と
と が存在することが知られている. 特に, 有界な凸多面体に対しては有限個の点
が存在することが知られている. 特に, 有界な凸多面体に対しては有限個の点 の凸結合全体, すなわち,
の凸結合全体, すなわち,
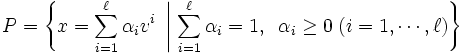
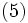
と表現でき, (5)で定義される集合は, 点集合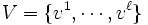 を含む (集合の包含関係の意味で) 最小な凸集合 (convex set)として定義される
を含む (集合の包含関係の意味で) 最小な凸集合 (convex set)として定義される の凸包 (convex hull) と一致する. 例えば,
の凸包 (convex hull) と一致する. 例えば,  の凸包である有界な凸多面体は
の凸包である有界な凸多面体は
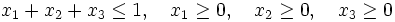
点集合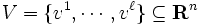 について, どの要素も他の要素たちのアフィン結合で表現できないとき, すなわち,
について, どの要素も他の要素たちのアフィン結合で表現できないとき, すなわち,

をみたすとき,  はアフィン独立(affinely independent)であるという.
はアフィン独立(affinely independent)であるという. 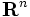 からは高々
からは高々 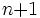 個のアフィン独立な点しか取れない. 集合
個のアフィン独立な点しか取れない. 集合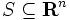 に含まれるアフィン独立な点集合で要素数最大のものを
に含まれるアフィン独立な点集合で要素数最大のものを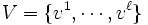 としたとき,
としたとき,  の次元は
の次元は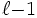 と定義する(次元は
と定義する(次元は の選び方に依存しないことを付記しておく). 先の例では,
の選び方に依存しないことを付記しておく). 先の例では,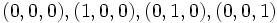 はアフィン独立であり, この凸包である三角錐の次元は
はアフィン独立であり, この凸包である三角錐の次元は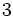 となる. 凸多面体
となる. 凸多面体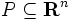 の次元が
の次元が  であるとき全次元的(full dimensional)という.
であるとき全次元的(full dimensional)という.
凸多面体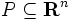 に対して, 超平面(hyperplane)
に対して, 超平面(hyperplane) 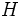 , すなわち, 非ゼロベクトル
, すなわち, 非ゼロベクトル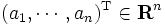 と
と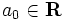 を用いて
を用いて
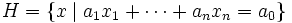
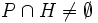 かつ
かつ 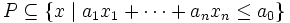
をみたすとき, 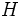 は
は の支持超平面 (supporting hyperplane) とよばれる. 支持超平面と凸多面体の共通部分も凸多面体である. この共通部分を凸多面体の面 (face) とよび, その次元が
の支持超平面 (supporting hyperplane) とよばれる. 支持超平面と凸多面体の共通部分も凸多面体である. この共通部分を凸多面体の面 (face) とよび, その次元が であるとき
であるとき 次元面(
次元面( -face,
-face,  dimensional face)とよぶ. 特に多面体より次元が
dimensional face)とよぶ. 特に多面体より次元が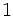 小さい面をファセット(facet),
小さい面をファセット(facet), 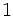 次元面を辺 (edge),
次元面を辺 (edge), 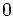 次元面を頂点 (vertex) とよぶ. 先の三角錐を例にすると, 不等式表現の4本に対応する面は
次元面を頂点 (vertex) とよぶ. 先の三角錐を例にすると, 不等式表現の4本に対応する面は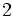 次元面 (ファセット) であり, 他に6個の
次元面 (ファセット) であり, 他に6個の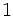 次元面 (辺) と4個の
次元面 (辺) と4個の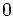 次元面 (頂点) を持つ. 一般に有界な凸多面体は頂点全体の凸包と一致し, 全次元的な凸多面体はファセットに対応した不等式で一意的に表現できる (不等式の両辺を正数倍しても同じものとみなす). 凸多面体自身と空集合を便宜上面とすると, 面全体は包含関係に関して束となり, 凸多面体の面束 (face lattice) とよばれる. 同型な面束を持つ凸多面体を互いに組合せ的に同型 (combinatorially equivalent) とよぶ. 束の順序関係を逆にしても束となるが, 任意の凸多面体の面束の順序関係を逆にした束と同型な面束を持つ凸多面体が常に存在し, これは, 元の凸多面体の双対多面体 (dual polytope) とよばれる.
次元面 (頂点) を持つ. 一般に有界な凸多面体は頂点全体の凸包と一致し, 全次元的な凸多面体はファセットに対応した不等式で一意的に表現できる (不等式の両辺を正数倍しても同じものとみなす). 凸多面体自身と空集合を便宜上面とすると, 面全体は包含関係に関して束となり, 凸多面体の面束 (face lattice) とよばれる. 同型な面束を持つ凸多面体を互いに組合せ的に同型 (combinatorially equivalent) とよぶ. 束の順序関係を逆にしても束となるが, 任意の凸多面体の面束の順序関係を逆にした束と同型な面束を持つ凸多面体が常に存在し, これは, 元の凸多面体の双対多面体 (dual polytope) とよばれる.
凸多面体は計算幾何学の重要な研究対象であるばかりでなく, 組合せ最適化問題の実行可能解全体を表現あるいは近似的に表現するための有益な道具である. 多面体理論の項目も参照されたい.
[1] A. Brondsted, An Introduction to Convex Polytopes, Springer-Verlag, 1980.
[2] G. L. Nemhauser and L. A. Wolsey, Integer and Combinatorial Optimization, Wiley-Interscience, 1988.
- convex polytopeのページへのリンク