内点法
【英】：interior point method
概要
線形計画問題に対するカーマーカー法によって触発され,発展した制約付き最適化問題の反復解法の総称. 実行可能領域の内部を通って最適解へ近づくのでこう呼ばれる.特に大規模問題に有効とされ, 凸計画問題, 半正定値計画問題等へも拡張されている. 主問題または双対問題のどちらか一方の実行可能領域に点列を生成する内点法を主内点法, 主問題および双対問題の双方の実行可能領域に点列を生成する内点法を主双対内点法と呼ぶ.
詳説
内点法(interior point method) は最適化問題の制約領域の境界上ではなく内部に, 最適解に収束する点列を生成する逐次反復解法である. 特に線形計画問題に対しては, 最適値に十分に近い近似解が得られれば, 変数次元の連立方程式を1回解く手間で最適解が得られることから, 内点法で最適解を得るまでに必要な計算の手間(算術演算回数)を算出することが可能であり, 多くの理論的な成果が報告されている. また実用面では, 特に大規模な問題に対して単体法よりも計算効率が 優れていることが確認されており, この解法を取り入れた商用コードも多く存在する. 線形計画問題以外への応用も積極的に行なわれており, 凸2次計画問題, 相補性問題, あるいは半正定値計画問題, 2次錐計画問題等の凸計画問題に対しても有効な解法であることが示されている.
1979年に提案された楕円体法は, 線形計画問題に対する初めての多項式時間解法であるが, 実用的な解法としては単体法に及ばなかった. これに対して1984年にATTベル研究所のカーマーカー(N. Karmarkar) によって提案された初めての内点法(interior point)であるカーマーカー法(Karmarkar's algorithm) [1] は, 多項式時間解法である上に, カーマーカー自身の計算機実験では 単体法を遥かに上回る結果であると報告された. この論文および報告を機として, 多くの最適化分野の研究者がこの解法に興味をもち, この結果多様なバリエーションが生み出された.
 |
(
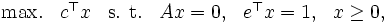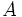は
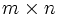行列,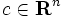 
, 
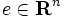は要素がすべて
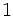のベクトル)を対象とし, 対数障壁関数を用いたポテンシャル関数(potential function) の値で最適解からの誤差を測り, 射影変換 (projective transformation) を用いて探索方向を決定するという特徴をもつ. 対数障壁関数を用いるという点で非線形計画法の一解法とも考えられるが, 着想, 解析共に従来の常識とは異なる斬新な解法であった. より一般的で記述が簡潔なアルゴリズムとして提案された解法が, アフィン変換法(affine scaling method) である. その後1988年に, ロシアの数学者ディキン(I. Dikin) が20年以上前の1967年に同じ解法を提案していたことが明かになり, 話題となった. アフィン変換法は実用的であり, 大域的収束性が示されているが, 解法の多項式時間性については未だ不明である.
他方, 従来のSUMT法, ホモトピー法, ニュートン法といった枠組を用いて内点法を構築する試みも行なわれた. 中でも大きな役割を果たしたのは, ゾンネべンド(Gy. Sonnevend)が提唱した中心パス(path of centers) であり, この概念を利用してレネガー(J. Renegar)はニュートン法を用いた初めての 多項式時間解法を提案した. さらに, 主問題と双対問題の双方を1つの問題とみなした場合の解析的 中心に関する研究も行なわれ, 主双対内点法(primal-dual interior point method) の提案へと結び付いた. 主双対内点法を改良した予測子修正子内点法(predictor-corrector interior point method) は, 現在もっとも普及している内点法の1つである. これらの解法については [5] 等を参照されたい.
内点法における大きな課題の1つは, 条件のよい許容領域内部の初期点をいかに用意するかという問題である. この課題の解決策として 非許容初期点内点法 (infeasible interior point method) や, 理論的にはさらに優れた 同次自己双対内点法 (homogeneous self-dual interior point method) が提案されており, 実装の際にはどちらかが用いられることが多い.
以上の解法の中で, アフィン変換法以外の解法は多項式時間解法であることが示されている. ネステロフとネミロフスキーは, 自己整合障壁関数の概念を導入した上で, 内点法という解法のクラスの中で, 多項式時間解法である解法からなる, 1つの大きなクラスを示した [2]. この研究は, 1990年代から活発に行なわれている, 半正定値計画問題や2次錐計画問題等に内点法を適用する研究の重要な基礎となっている.
読書案内
近年内点法が記述された教科書も多く出版されている. [12] は内点法を総合的に扱った和書である. 線形計画法のみならず, 半正定値計画問題, 非線形計画問題に対する内点法についも述べている. その他の洋書の多くは主双対内点法と非許容初期点内点法を基本とした内容であるが, カーマーカー法については [3], [9], アフィン変換法については [4], [6], 同次自己双対内点法については, [6], [10] 等にそれぞれ詳しく述べられている. [8], [9], [10] はそれぞれ線形計画法の教科書であり, 図表が多く入門的な内容であるが, [8] は単体法, [9] は内点法を包括する理論, [10] は実装 にそれぞれ重きを置いている点が特徴である. また, 内点法に関する論文の多くは, インターネットを通じて入手可能である [11].
[1] K. Karmarkar, "A New Polynomial-Time Algorithm for Linear Programming," Combinatorica, 4 (1984), 373-395.
[2] Y. Nesterov and A. S. Nemirovskii, Interior Point Polynomial Algorithms in Convex Programming, SIAM, 1994.
[3] S.-C. Fang and S. Puthenpra, Linear Optimization and Extentions Prentice Hall, 1993.
[4] R. Saigal, Linear Programming: A Modern Integrated Analysis Kluwer Academic Publishers, 1995.
[5] J. Wright, Primal-Dual Interior-Point Methods, SIAM, 1996.
[6] T. Terlaky, eds., Interior Point Methods of Mathematical Programming, Kluwer Academic Publishers, 1996.
[7] Y. Ye, Interior Point Algorithms: Theory and Analysis, Jhon Wiley & Sons, 1997
[8] D. Bertsimas and J. N. Tsisiklis, Introduction to Linear Optimization, Athena Scientific, 1997.
[9] C. Roos, T. Terlaky and J.-Ph. Vial Theory and Algorithns for Linear Optimization, John Wiley & Sons, 1997.
[10] R. J. Vanderbei, Linear Programming: Foundations and Extensions, Kluwer Academic Publishers, 1998.
ないてんほうと同じ種類の言葉
- ないてんほうのページへのリンク
