カーマーカー法
【英】：Karmarkar's algorithm
1984年にカーマーカーが提案した, 初めての内点法. 「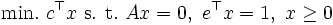
(
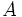は
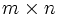行列,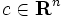 
, 
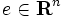は 要素がすべて
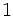のベクトル)」の線形計画問題に対して, 「(1) 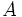の階数は
, (2)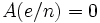
, (iii)最適値は
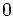」の仮定の下で, 初期点 
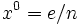から最適解に収束する点列 
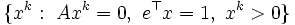を生成する多項式時間解法. 任意の線形計画問題から, 上記の仮定を満す人工問題が生成でき, 元の問題の最適性が判定できる.
| 非線形計画： | NP困難 エラーバウンド カルーシュ・キューン・タッカー条件 カーマーカー法 ダンツィク・ウルフ分解法 ニュートン法 フェンシェルの双対性 |
| 線形計画： | 2次錐計画 NP困難 アフィン変換法 カーマーカー法 シンプレックス法 ポテンシャル関数 中心パス |
カーマーカーのアルゴリズム
(Karmarkar's algorithm から転送)
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/05/08 08:10 UTC 版)
カーマーカーのアルゴリズム（英: Karmarkar's algorithm）とは1984年、ナレンドラ・カーマーカーにより発見された線形計画問題の解法である。このアルゴリズムは、しばしば、カーマーカー法（英: Karmarkar's method）とも呼ばれる。また、このアルゴリズムを発明とする特許が米国や日本で出願され、請求特許は時折カーマーカー特許 (Karmarkar's patent) とも呼称される。
カーマーカーのアルゴリズムは、線形計画問題に対する多項式時間アルゴリズムで初めての実用的なものである。楕円体法も多項式時間アルゴリズムであるが、実用上の効率は良くない。
カーマーカーのアルゴリズムは内点法の一種である。内点法は、候補解を実行可能領域の境界に沿って更新する単体法とは異なり、実行可能領域の内部を通るよう更新する。この更新は解の精度を定数倍改善し、これを繰り返すことで最適解（optimal solution）に収束する[1]。
アルゴリズム
以下の線形計画問題を考える。
-
maximize
Optimization computes maxima and minima.
| 一般 | |
|---|---|
| 微分可能 |
| 凸最小化 | |||||||
|---|---|---|---|---|---|---|---|
| 線形 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
||||
| ネットワークフロー (最大流問題) |
 |
この項目は、応用数学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています。 |
 |
この項目は、法分野に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（P:法学/PJ:法学）。 |
- Karmarkar's algorithmのページへのリンク
