アフィン変換法
アフィンスケーリング法
(アフィン変換法 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/12 04:18 UTC 版)

アフィンスケーリング法(アフィンスケーリングほう、アフィン変換法、アフィンへんかんほう、英: affine scaling)とは、数理最適化において線形計画問題を解くためのアルゴリズムである。これは内点法であり、1967年ソヴィエト連邦の数学者 I.I.ディキンによって編み出され、1980年代にアメリカ合衆国で再発見された解法である。
歴史
アフィンスケーリング法は1967年、Doklady Akademii Nauk SSSR にロシア科学アカデミー、エネルギーシステム研究所[注釈 1]の I.I.ディキンによって提案、1974年に収束性を証明されて以降再度の発見を辿ることとなる[1]。ディキンの業績は線形計画問題に対する初の実用的多項式時間アルゴリズムであるカーマーカー法が1984年に編み出されるまでほとんど知られることがなかった。このカーマーカー法の目新しさと計算複雑性によってカーマーカー法の高度な技法をより単純な技法で実現するための研究に多くの研究者が興味を持ち始めた。
以降、カーマーカー法の類似の解法がいくつかのグループによって独立に提案された。IBMの E.R.Barnes[2]、AT&Tのロバート・ヴァンダーベイらのグループ[3]、その他いくつかのチームがカーマーカー法の射影変換をアフィン変換に置き換えた内点法を提案した。これらの提案から数年が経ってから、彼らによって提案されたアフィンスケーリング法が実際にはディキンの研究の再発見に過ぎなかったことが判明した[1][4]。再発見を通じて Barnes およびヴァンダーベイらのみがアフィンスケーリング法の収束性について示すことができた。またカーマーカーもアフィンスケーリング法を編み出していたが、カーマーカー法と同様の収束性をもつ解法であると誤った認識をしていたとされている[5]:346。
アルゴリズム
アフィンスケーリング法は二つの段階から構成されており、一段階目で実行可能点を求めて、二段階目は実行可能領域の内部を厳密に通って真の最適解を求める。
二つの段階ともに線形計画問題の等式標準形について考える:
- アフィン変換法のページへのリンク
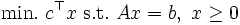 (
(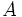 は
は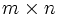
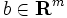 ,
, 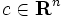 )」
)」
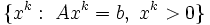 である
である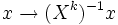 (
( は
は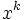 の
の
