線形計画
【英】:linear programming
概要
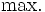 |
 あるいは, あるいは, 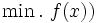 |
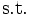 |
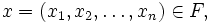 |
において, 目的関数  が線形であり, かつ, 実行可能集合
が線形であり, かつ, 実行可能集合 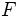 が線形等式と線形不等式を用いて表現されている問題.この問題への定式化, および, 解法を含めて線形計画と呼ぶ.
が線形等式と線形不等式を用いて表現されている問題.この問題への定式化, および, 解法を含めて線形計画と呼ぶ.
詳説
線形計画(linear programming)(線形計画法, 線形計画問題)は, 複数の等式あるいは不等式で与えられる線形制約のもとで, 目的関数(objective function)と呼ばれる線形関数を最大化(または最小化)する問題である. 線形計画問題は通常以下の形式により表現される.
|
|
ここで, 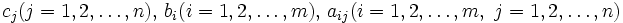 は実数,
は実数, 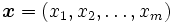 は
は 個の変数からなる
個の変数からなる 次元ベクトルである. すべての線形計画問題は, 簡単な変換により, この形式に帰着される. 問題(P)の制約条件を満たす
次元ベクトルである. すべての線形計画問題は, 簡単な変換により, この形式に帰着される. 問題(P)の制約条件を満たす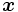 を実行可能解(feasible solution)と呼び, 実行可能解のなかで目的関数を最大にするものを最適解と呼ぶ.
を実行可能解(feasible solution)と呼び, 実行可能解のなかで目的関数を最大にするものを最適解と呼ぶ.
実社会における多くの問題は線形計画問題として定式化できる. 線形計画の応用は, 初期の頃は, 軍事, 経済学やゲーム理論が中心であったが, 次第にその重点が産業の分野へと移行された [2, 3]. 1947年にダンツィク(G. B. Dantzig)[2] によって提案された単体法(simplex method)は, コンピュータの急速な発展と大規模な線形方程式を処理する技術の向上とあいまって, 線形計画問題に対する極めて実用的な解法となっている. しかし, 単体法は Klee-Minty [4] により, 問題の入力サイズ(変数の個数と制約の本数)に関する多項式時間解法ではないことが指摘された. カチヤン(L. G. Khachian)は楕円体法を提案し, 最初の多項式時間解法を与えた. カーマーカー法およびその後開発された内点法は, 超大規模な線形計画問題に対し, 理論および実用の両面において, 単体法より優れた解法として認められている.
以下では, 線形計画の理論で重要な役割を果たす双対問題(dual problem), 双対定理(duality theorem)および相補性定理(complementarity slackness theorem)について述べる.
各々の線形計画問題(P)には, 双対問題と呼ばれる以下の線形計画問題(D)を対応させることができる:
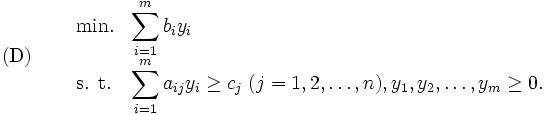 |
ここで, 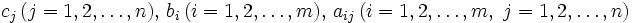 は元の問題(P)で与えられたデータと同一である. 元の問題(P)は主問題, 問題(D)は主問題(P)に対する双対問題と呼ばれる. 双対問題の双対問題が主問題になることは, 問題(D)を問題(P)の形式に書き直すことにより容易に示せる. 主問題と双対問題の実行可能解について, 次のようなことが言える.
は元の問題(P)で与えられたデータと同一である. 元の問題(P)は主問題, 問題(D)は主問題(P)に対する双対問題と呼ばれる. 双対問題の双対問題が主問題になることは, 問題(D)を問題(P)の形式に書き直すことにより容易に示せる. 主問題と双対問題の実行可能解について, 次のようなことが言える.
さらに, 以下の双対定理と相補性定理が示すように, 主問題と双対問題のいずれか一方の最適解は, 他方の問題の最適解に関する情報を含む.
双対定理: 主問題か双対問題のいずれか一方が最適解をもつならば, 他方もまた最適解をもち, それらの目的関数値は一致する. また, いずれか一方の問題の実行可能解に対する目的関数値が有界でなければ, 他方の問題は実行可能解をもたない.
相補性定理: 主問題の実行可能解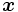 と双対問題の実行可能解
と双対問題の実行可能解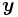 がそれぞれの問題の最適解であるための必要十分条件は, 以下の2条件(i),(ii)が成り立つことである.
がそれぞれの問題の最適解であるための必要十分条件は, 以下の2条件(i),(ii)が成り立つことである.
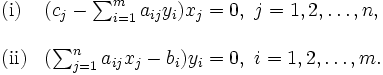 |
これらの最適性条件を次のように言い換えることができる. いずれか一方の問題の 番目の制約式が不等号で成り立つならば, 他方の問題において対応する変数の値はゼロになる. また, いずれか一方の問題の
番目の制約式が不等号で成り立つならば, 他方の問題において対応する変数の値はゼロになる. また, いずれか一方の問題の 番目の変数の値が正ならば, 他方の問題においてそれに対応する制約式は等号で成り立つ.
番目の変数の値が正ならば, 他方の問題においてそれに対応する制約式は等号で成り立つ.
[1] V. Chvátal, Linear Programming, W. H. Freeman and Company, 1983, 阪田省二郎, 藤野和建 訳, 『線形計画法』上, 下, 啓学出版.
[2] G. B. Dantzig, Linear Programming and Extensions, Princeton University Press, 1963.
[3] S. I. Gass, Linear Programming and Extensions, MaGram-Hill, 1975.
[4] V. Klee and G. J. Minty "How good is the simplex algorithm?" in Inequalities-III, O. Shisha, eds., Academic Press, 159-175, 1989.
- Linear Programmingのページへのリンク
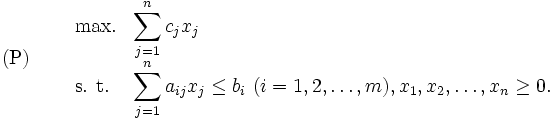
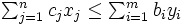 が
が