半正定値計画
【英】:semidefinite programming
概要
線形計画を実対称行列の空間に拡張したもの.等質自己双対錐上の線形計画問題の1つでもある.半正定値計画は
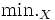 | 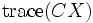 |
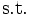 | 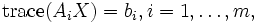 |
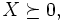 |
で表される.ただし, 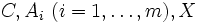 は
は  実対称行列,
実対称行列,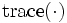 は行列のトレース,
は行列のトレース,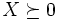 は
は 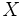 が半正定値であることを表す.
が半正定値であることを表す.
詳説
問題: 半正定値計画は線形計画(linear programming)を実対称行列の空間に拡張したものである. 次のような定式化が一般的である.
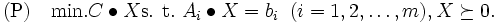 |
ただし, 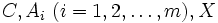 は
は  実対称行列,
実対称行列, 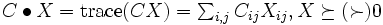 は
は  が半正定値(正定値)であることを表す. 半正定値計画
が半正定値(正定値)であることを表す. 半正定値計画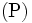 は凸計画問題(convex programming)であり, 双対問題は次のようになる.
は凸計画問題(convex programming)であり, 双対問題は次のようになる.
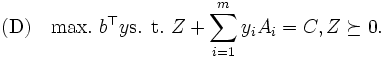 |
双対性: 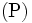 と
と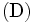 の間に次の弱双対定理が成り立つことは容易に分かる.
の間に次の弱双対定理が成り立つことは容易に分かる.
半正定値計画では線形計画とは異なり, 一般に強双対定理は成り立たない. 主問題または双対問題に最適解が存在しないことや, 両者の最適値が一致しないことがある. 強双対定理が成り立つためには何らかの条件が必要である. よく使われる条件は次のようなものである.
強双対定理. もし 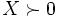 ,
, 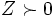 なる許容解
なる許容解  および
および  が存在すれば,
が存在すれば, 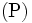 と
と 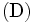 の最適値は一致し, 両者に最適解が存在する.
の最適値は一致し, 両者に最適解が存在する.
最適解があっても強相補性を持つ解が存在しない場合があり, また, 退化に関しても特有の定義が使われることが多い. 半正定値計画における退化および強相補性に関しては [1] を参照せよ.
解法: 半正定値計画 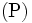 には,
には, 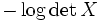 が
が -自己整合障壁関数(self-concordant barrier function)となることが知られており, 主内点法(interior point method)を使って効率良く解くことができる [3]. また半正定値計画は, 等質自己双対錐(homogeneous self-dualcone, symmetric cone, self-scaled cone)上の線形計画問題とも見ることができ, 主双対内点法で効率良く解くことができる[4]. 以下, 現在最も有力な解法とみられている主双対パス追跡法について説明する.
-自己整合障壁関数(self-concordant barrier function)となることが知られており, 主内点法(interior point method)を使って効率良く解くことができる [3]. また半正定値計画は, 等質自己双対錐(homogeneous self-dualcone, symmetric cone, self-scaled cone)上の線形計画問題とも見ることができ, 主双対内点法で効率良く解くことができる[4]. 以下, 現在最も有力な解法とみられている主双対パス追跡法について説明する.
半正定値計画 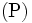 および
および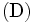 の中心パス(path of centers)上のパラメタ
の中心パス(path of centers)上のパラメタ 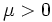 に対応する点
に対応する点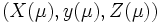 は次を満たす.
は次を満たす.
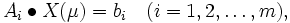 |
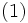 |
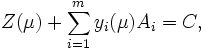 |
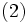 |
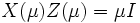 |
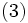 |
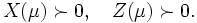 |
ここで 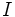 は恒等行列である. 主双対パス追跡法では
は恒等行列である. 主双対パス追跡法では 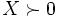 ,
, 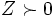 なる現在点が与えられたとして, 適当な
なる現在点が与えられたとして, 適当な 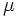 を定めて(1), (2), (3)に対するニュートン方向を探索方向とする. ところが一般に
を定めて(1), (2), (3)に対するニュートン方向を探索方向とする. ところが一般に  は対称行列ではないので, 式 (1), (2), (3) の左辺
は対称行列ではないので, 式 (1), (2), (3) の左辺 右辺を一つの関数と見た場合, その関数は
右辺を一つの関数と見た場合, その関数は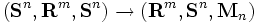 (ここで
(ここで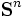 は
は 対称行列の集合,
対称行列の集合, 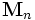 は
は 行列の集合を表す.) となり, 普通の意味でニュートン方向を定義できない. この問題を克服するためにいろいろな手段が考えられ, その結果様々な探索方向が提案されている. 以下に, 比較的初期に提案された探索方向を四つ挙げる. (方向の名前は, 提案した論文の著者名に由来している.)
行列の集合を表す.) となり, 普通の意味でニュートン方向を定義できない. この問題を克服するためにいろいろな手段が考えられ, その結果様々な探索方向が提案されている. 以下に, 比較的初期に提案された探索方向を四つ挙げる. (方向の名前は, 提案した論文の著者名に由来している.)
理論的には, これらの探索方向を使うと, 許容解 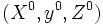 から出発した場合,
から出発した場合, 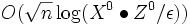 回の反復で双対ギャップを
回の反復で双対ギャップを 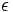 以下に減らすことができることが知られている. 詳しくは [6] 参照.
以下に減らすことができることが知られている. 詳しくは [6] 参照.
半正定値計画の解法としては, 単体法はあまり研究されていない. 係数行列に構造のある問題に対しては, 固有値に関する最適化問題に直して微分不可能最適化に対する手法を適用することも試みられている.
応用: 半正定値計画の応用で最もORと関係が深いのは組合せ最適化問題(combinatorial optimization)および多項式最適化問題の半正定値計画緩和(semidefinite programming relaxzation)であろう. NP困難(NP-hard)な組合せ最適化問題または多項式最適化問題(polynomial optimization problem)の緩和問題として半正定値計画を使うと, 元問題の最適値の良い近似値を多項式時間で求められる. 行列の固有値に関する最適化問題, 例えば固有値の和の最小化なども半正定値計画で表現できる. また, 制御理論における線形行列不等式(linear matrix inequality)は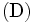 と等価である. 半正定値計画の応用については [2], [5], [6] を参照されたい.
と等価である. 半正定値計画の応用については [2], [5], [6] を参照されたい.
[1] F. Alizadeh, J. P. A. Haeberly and M. L. Overton, "Complementarity and nondegeneracy in semidefinite programming," Mathematical Programming, 77 (1997) 111-128.
[2] M. X. Goemans, "Semidefinite programming in combinatorial optimization," Mathematical Programming, 79 (1997) 143-161.
[3] Y. E. Nesterov and A. S. Nemirovskii Interior Point Polynomial Methods in Convex Programming : Theory and Algorithms, SIAM Publications, Philadelphia, 1993.
[4] Y. E. Nesterov and M. J. Todd, "Primal-dual interior-point methods for self-scaled cones," SIAM Journal on Optimization, 8 (1998) 324-364.
[5] L. Vandenberghe and S. Boyd, "Semidefinite programming," SIAM review, 38 (1996) 49-95.
半正定値計画問題
(半正定値計画 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/17 02:51 UTC 版)
半正定値計画問題(はんせいていちけいかくもんだい、英: semidefinite programming)とは、半正定値行列全体によって作られる凸錐体上での凸最適化問題(convex optimization)の一つである。
半正定値計画問題は近年いくつかの理由で成長している最適化の一分野である。その理由として多くの実用例が考えられることがあげられるが、特にオペレーションズ・リサーチや組み合わせ最適化などの分野で広く研究が行われている。自動制御理論の分野では半正定値計画問題が線形不等式制約のもとで行われることが多い。半正定値計画問題は、凸錐体上の凸最適化問題の一種であり、内点法などにより効率よく解を与えることが可能であることも、応用が期待される一要因となっている[1]。また半正定値計画問題の階層化により多項式最適化問題が近似的に解けるほか、複雑系の最適化にも応用が可能である。
定義
線形計画問題はある空間上で多面体に含まれるような実数の組に対して、線形の目的関数を最小化・最大化する問題である。ここで、多面体というのは、より厳密には凸集合であるということを指す。一方で、半正定値計画問題においては、ベクトルの内積を最適化する。特に、一般的な半正定値計画問題は、数理計画問題の形式として、以下のように定義される(ただし、 は内積を表す)。
さらに、この問題は半正定値行列の作る凸錐体上の問題として書き直すことができる。大きさが の行列 が 本のベクトル を用いて で表されるとき、行列をグラム行列といい、この行列は半正定値となることが知られている。
ここで、 を実対称行列全体の空間とする。この空間では内積を (ただし、 は行列の跡を表す)と定義することができて、これを用いると、前述のベクトルを用いた半正定値計画問題が次の形で書き直せる。
ただし、 とは行列 が半正定値行列であることを表す。この式において は を、 は の行列で を成分に持つ。
双対性
双対問題の定義
線形計画問題と同様、半正定値計画問題も双対問題を考えることが可能で、
という半正定値計画問題の双対問題は
という形で与えられる。なお大きさが等しい2つの正方行列 に対して、 とは、 と同義である。
弱双対性
弱双対定理とは、半正定値計画問題の主問題と双対問題の許容解の関係を表す定理であり、主問題の許容解が双対問題の上界となり、双対問題の許容解が主問題の下界となるというものである。 これは、次の式により示される。
最後の不等式が成立するのは、行列の内積を取っている2つの行列が、どちらも半正定値行列であるためである。
強双対性
スレーター条件と呼ばれる条件の下では、主問題と双対問題の最適解が一致することが知られている。これを強双対性という。線形計画問題と違い、半正定値問題は、すべての問題が強双対性を満たすわけではなく、一般には双対問題の最適解は主問題の最適解よりも小さい。強双対性は次の2つの性質により言い表される。
- 主問題が下に有界であり、かつ内点許容解をもつとき、双対問題が最適解を持つ。
- 双対問題が上に有界であり、かつ内点許容解をもつとき、主問題が最適解を持つ。
この2つの性質から、主問題と双対問題の両方が最適解を持ち、それらが一致することが言える。
脚注
参考文献
- 藤江哲也 著「14.3 半正定値計画緩和」、久保幹雄、田村明久、松井知己 編『応用数理計画ハンドブック 普及版』朝倉書店、2012年。ISBN 9784254270211。 NCID BB09691604。 OCLC 820781686。
- 田村明久、村松正和『最適化法』共立出版株式会社、2002年、176-194頁。 ISBN 9784320016163。 NCID BA56453921。 OCLC 676380575。
- 半正定値計画のページへのリンク
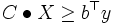 .
.
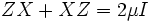 と
と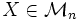 として
として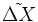 を
を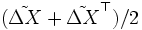 と
と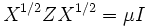 と
と
![{\displaystyle {\begin{array}{rl}{\displaystyle \min _{x^{1},\ldots ,x^{n}\in \mathbb {R} ^{n}}}&{\displaystyle \sum _{i,j\in [n]}c_{i,j}(x^{i}\cdot x^{j})}\\{\text{subject to}}&{\displaystyle \sum _{i,j\in [n]}a_{i,j,k}(x^{i}\cdot x^{j})\leq b_{k}\qquad \forall k}.\\\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c71a45b72d5c74a5a71aa61749d4909f464bf8c)






















