戦略形ゲーム
【英】:strategic form game
概要
プレイヤーの集合, 各プレイヤーのとりうる戦略の集合, および, 各プレイヤーの利得関数を記述することによりゲームを表現する形式. 標準形ゲームともいう.
詳説
ゲームに参加するプレイヤーの集合を , 各プレイヤー
, 各プレイヤー のとりうる戦略の全体を
のとりうる戦略の全体を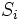 , および
, および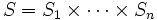 上で定義された各プレイヤー
上で定義された各プレイヤー のフォンノイマン・モルゲンシュテルン効用関数 (von Neumann-Morgenstern utility function) を
のフォンノイマン・モルゲンシュテルン効用関数 (von Neumann-Morgenstern utility function) を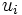 とするとき,
とするとき,
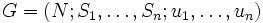
を戦略形ゲーム (game in strategic form) または標準形ゲーム (game in normal form) という.  と
と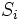 がすべて有限集合であるとき,
がすべて有限集合であるとき,  を有限ゲームという. 効用関数
を有限ゲームという. 効用関数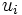 は, また利得関数 (payoff function) ともいい, その値を利得という.
は, また利得関数 (payoff function) ともいい, その値を利得という.
戦略形で書かれたゲームは, 特にことわらない限り非協力ゲームである. 戦略の数が有限な2人ゲームは次のような利得双行列 (payoff bimatrix) で表現することができるので, 双行列ゲーム (bimatrix game) ということがある.

ここに, 縦の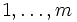 はプレイヤー1の戦略, 横の
はプレイヤー1の戦略, 横の はプレイヤー2の戦略であり,
はプレイヤー2の戦略であり, 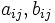 は, プレイヤー1, 2が各々戦略
は, プレイヤー1, 2が各々戦略 をとったときの, プレイヤー1, 2の利得である.
をとったときの, プレイヤー1, 2の利得である. 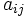 を成分とする行列を
を成分とする行列を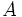 ,
, 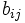 を成分とする行列を
を成分とする行列を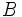 と表し, 利得双行列を簡単に
と表し, 利得双行列を簡単に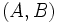 と表す. すべての
と表す. すべての について,
について, 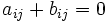 となる場合が2人ゼロ和ゲーム (two-person zerosum game) の戦略形である. 行列
となる場合が2人ゼロ和ゲーム (two-person zerosum game) の戦略形である. 行列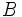 は
は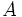 の符号を変えたものであり, 行列
の符号を変えたものであり, 行列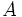 だけでゲームを記述できるので2人ゼロ和ゲームを行列ゲーム (matrix game) ということもある.
だけでゲームを記述できるので2人ゼロ和ゲームを行列ゲーム (matrix game) ということもある.
双行列ゲーム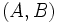 において, 各プレイヤーの混合戦略 (mixed strategy) を各々
において, 各プレイヤーの混合戦略 (mixed strategy) を各々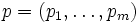 ,
, 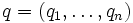 とすると, 各プレイヤーの利得の期待値 (期待利得) は各々
とすると, 各プレイヤーの利得の期待値 (期待利得) は各々 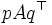 および
および 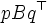 で与えられる.
で与えられる. 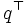 は
は の転置ベクトルを表す. また, 混合戦略に対してもとの戦略を純戦略 (pure strategy) という. ナッシュ均衡
の転置ベクトルを表す. また, 混合戦略に対してもとの戦略を純戦略 (pure strategy) という. ナッシュ均衡 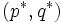 は, 非協力ゲーム理論の項で述べた定義によって,
は, 非協力ゲーム理論の項で述べた定義によって,
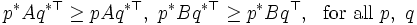
をみたす混合戦略の組である. とくに, ゼロ和ゲームでは, 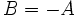 であるから
であるから
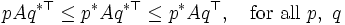
となり, これからミニマックス定理 (minimax theorem)
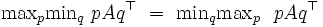
が導かれ, さらにこの値は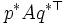 に等しい. 左辺の値をマックスミニ値 (maxmin value), 右辺の値をミニマックス値(minimax value), さらに, この共通の値をゲームの値 (value of a game) という. また, このときの戦略
に等しい. 左辺の値をマックスミニ値 (maxmin value), 右辺の値をミニマックス値(minimax value), さらに, この共通の値をゲームの値 (value of a game) という. また, このときの戦略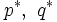 を各々マックスミニ戦略 (maxmin strategy), ミニマックス戦略 (minimax strategy) という.
次に示すのは, 左が囚人のジレンマ (prisoner's dilemma), 右が逢い引きのジレンマ (battle of the sexes) という名で知られる有名な双行列ゲームである.
を各々マックスミニ戦略 (maxmin strategy), ミニマックス戦略 (minimax strategy) という.
次に示すのは, 左が囚人のジレンマ (prisoner's dilemma), 右が逢い引きのジレンマ (battle of the sexes) という名で知られる有名な双行列ゲームである.
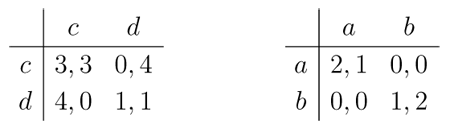
囚人のジレンマでは, 純戦略の組 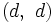 のみが, また, 逢い引きのジレンマでは, 純戦略の組
のみが, また, 逢い引きのジレンマでは, 純戦略の組 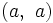 および
および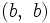 と, 混合戦略の組
と, 混合戦略の組 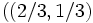 ,
, 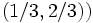 がナッシュ均衡である. とくに, 囚人のジレンマのナッシュ均衡では, 戦略
がナッシュ均衡である. とくに, 囚人のジレンマのナッシュ均衡では, 戦略 は相手のすべての戦略に対する最適反応 (best reply) となっている. このようなナッシュ均衡を, 支配戦略均衡 (dominant strategy equilibrium) ということがある. 逢い引きのジレンマには支配戦略は存在しない. また, 逢い引きのジレンマでは, 混合戦略ナッシュ均衡における利得の組
は相手のすべての戦略に対する最適反応 (best reply) となっている. このようなナッシュ均衡を, 支配戦略均衡 (dominant strategy equilibrium) ということがある. 逢い引きのジレンマには支配戦略は存在しない. また, 逢い引きのジレンマでは, 混合戦略ナッシュ均衡における利得の組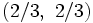 は, たとえば純粋戦略ナッシュ均衡
は, たとえば純粋戦略ナッシュ均衡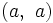 における利得の組
における利得の組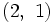 に対して各プレイヤーについて劣っている. このとき, 利得の組
に対して各プレイヤーについて劣っている. このとき, 利得の組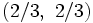 は
は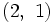 にパレート支配 (Pareto dominate) されるという.
にパレート支配 (Pareto dominate) されるという.
戦略形ゲームにおいて, もし, 各プレイヤーが共通の偶然機構にもとづいて戦略を選ぶことが許されているならば, 各プレイヤーは互いに相関した行動をとることができる. このような戦略を相関戦略 (correlated strategy) という. たとえば, 逢い引きのジレンマで, コインを投げて表が出たら戦略の組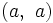 , 裏が出たら
, 裏が出たら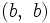 とすることに2人が合意したとしよう. つまり, 2人とも, 表が出たら
とすることに2人が合意したとしよう. つまり, 2人とも, 表が出たら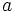 をとり, 裏が出たら
をとり, 裏が出たら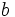 をとるという相関戦略をとるものとする. このような合意がナッシュ均衡になるとき, すなわち, 相関戦略の組がナッシュ均衡となっているとき, これを相関均衡 (correlated equilibrium) という. 上に述べた相関戦略の組は相関均衡であり, 2人の期待利得はともに
をとるという相関戦略をとるものとする. このような合意がナッシュ均衡になるとき, すなわち, 相関戦略の組がナッシュ均衡となっているとき, これを相関均衡 (correlated equilibrium) という. 上に述べた相関戦略の組は相関均衡であり, 2人の期待利得はともに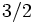 となることが容易にわかる. また, 混合戦略均衡は互いに独立な相関戦略からなる相関均衡にほかならない. 相関均衡の正式な定義については, たとえば [3] など参照.
となることが容易にわかる. また, 混合戦略均衡は互いに独立な相関戦略からなる相関均衡にほかならない. 相関均衡の正式な定義については, たとえば [3] など参照.
以上のゲームでは, 戦略形 についての知識がすべてのプレイヤーの間で共有知識 (common knowledge) であると仮定されており, これらは完備情報ゲーム (game with complete information) といわれている. 他方, 不完備情報ゲームはハルサーニ(J. C. Harsanyi) [2] の定式化によって分析できるようになった. たとえば, 利得関数
についての知識がすべてのプレイヤーの間で共有知識 (common knowledge) であると仮定されており, これらは完備情報ゲーム (game with complete information) といわれている. 他方, 不完備情報ゲームはハルサーニ(J. C. Harsanyi) [2] の定式化によって分析できるようになった. たとえば, 利得関数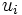 に関する情報が不完備な場合は, まず有限個のパラメター
に関する情報が不完備な場合は, まず有限個のパラメター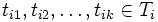 を導入し, プレイヤー
を導入し, プレイヤー の利得関数は, そのタイプによって, 有限個の利得関数
の利得関数は, そのタイプによって, 有限個の利得関数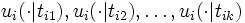 (以下, まとめて
(以下, まとめて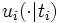 と表す. )のうちのどれか1つに定まる, と定式化し直すことにより,
と表す. )のうちのどれか1つに定まる, と定式化し直すことにより, 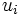 に関する不完備情報を表現する. この
に関する不完備情報を表現する. この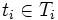 をプレイヤー
をプレイヤー のタイプという. 各プレイヤー
のタイプという. 各プレイヤー は自分はどのタイプであるかを知っているが, 他のプレイヤーのタイプは知らない. ただし, 他のすべてのプレイヤーのタイプ
は自分はどのタイプであるかを知っているが, 他のプレイヤーのタイプは知らない. ただし, 他のすべてのプレイヤーのタイプ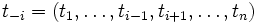 について条件付き確率
について条件付き確率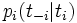 によって
によって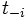 を推測することができるとする. こうして, 新たな戦略形ゲーム
を推測することができるとする. こうして, 新たな戦略形ゲーム
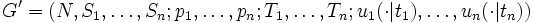
がえられる. これをベイジアンゲーム (Bayesian game) という. また, 関数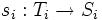 をベイジアンゲームの戦略という. すなわち, プレイヤー
をベイジアンゲームの戦略という. すなわち, プレイヤー は, 自分のタイプを知ってはいるが, どのタイプであったとしてもそのもとでの行動を指定しておくことがこの場合の戦略である. するとナッシュ均衡は, すべてのプレイヤー
は, 自分のタイプを知ってはいるが, どのタイプであったとしてもそのもとでの行動を指定しておくことがこの場合の戦略である. するとナッシュ均衡は, すべてのプレイヤー とタイプ
とタイプ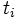 および
および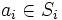 について次の条件をみたす戦略の組
について次の条件をみたす戦略の組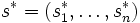 である. この戦略の組を, ベイジアンナッシュ均衡 (Bayesian Nash equilibrium) という.
である. この戦略の組を, ベイジアンナッシュ均衡 (Bayesian Nash equilibrium) という.

ただし, 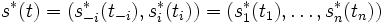 である. ベイジアンゲームは, 80年代以降, 情報経済学や産業組織論などの新しい分野の発展に大きく貢献している. これについてはたとえば, [1] を参照.
である. ベイジアンゲームは, 80年代以降, 情報経済学や産業組織論などの新しい分野の発展に大きく貢献している. これについてはたとえば, [1] を参照.
[1] R. Gibbons, Game Theory for Applied Economists, Princeton University Press, 1992. /福岡正夫, 須田伸一, 『経済学のためのゲーム理論入門』, 創文社, 1995.
[2] J. C. Harsanyi, "Games with Incomplete Information Played by `Bayesian' Players, parts I, II and III", Management Science, 14 (1967-8), 159-182, 320-334, 486-502.
[3] M. J. Osborne and A. Rubinstein, A Course in Game Theory, MIT Press, 1994.
標準型ゲーム
(戦略形ゲーム から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/08/31 18:55 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。(2009年10月)
|
標準型ゲーム(ひょうじゅんがたげーむ、英: normal form game)は、展開型ゲームと並び非協力ゲームの基本的表現形式であり、プレイヤー集合、戦略空間、利得関数の 3 つの要素から構成される。展開型ゲームは標準型ゲームより多くの情報を含んでおり、すべての展開型ゲームは標準型ゲームに変換することができる。一方、標準型ゲームは同時手番ゲームとみなすことができる。プレイヤー集合及び戦略空間が有限集合のとき、ナッシュ均衡および完全均衡が混合戦略の範囲で存在することが知られている(ナッシュの定理)。
標準型ゲームは、正規形ゲームあるいは戦略型ゲーム(英: strategic form game)とも呼ばれる。
定義
標準型ゲームとは 3 つ組 G = (N, S, u) として表現され、それぞれ、N はプレイヤーの集合、
均衡概念
均衡概念およびそれに準じた概念のうち、代表的なものを以下に挙げる。
参考文献
- ^ “双行列ゲームとは何? Weblio辞書”. 2021年1月24日閲覧。
- ^ 渡辺隆裕『ゼミナール ゲーム理論入門』日本経済新聞出版、2008年4月7日。ISBN 978-4-532-13346-7。
関連項目
- 戦略形ゲームのページへのリンク
