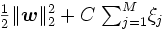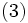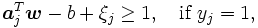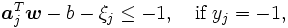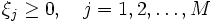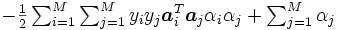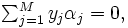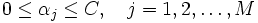サポート・ベクター・マシーン
【英】:support vector machine
概要
線形な判別関数を求める教師付き機械学習法のひとつである. 判別関数の複雑さの度合いと判別の精度の双方を考慮した, 二次計画問題として定式化され,判別関数が算出される. ここで用いられる二次計画問題の構造に特化した最適化アルゴリズムが知られており, データ数が多い大規模な判別問題でも, 多くの場合,実用的な速度で最適化を行うことが可能である. また,カーネル関数を用いることで, 非線形な判別関数を算出することも可能である.
詳説
サポート・ベクター・マシン (SVM) は, 判別関数を求める教師付き学習法のひとつである.
今,  個の属性を持ったデータが
個の属性を持ったデータが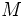 個与えられており,これを,
個与えられており,これを, 次元空間
次元空間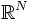 の点
の点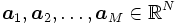 と考える. 各点
と考える. 各点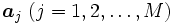 は2種類のクラスのいづれか一方に属しており, 対応する2値のラベル
は2種類のクラスのいづれか一方に属しており, 対応する2値のラベル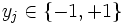 が与えられているとする. このとき, ラベルの値にしたがって点を判別する2クラスの判別問題を考える.
が与えられているとする. このとき, ラベルの値にしたがって点を判別する2クラスの判別問題を考える.
SVMでは線形関数を用いた判別を行う.  次元の法線ベクトル
次元の法線ベクトル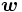 および実数
および実数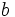 で定まる線形関数を
で定まる線形関数を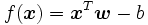 とすれば, 与えられたデータおよびラベルにしたがって,
とすれば, 与えられたデータおよびラベルにしたがって,
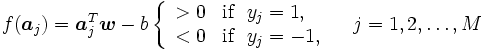
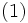
となるベクトル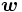 とスカラ
とスカラ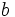 を次に示す最適化問題を解くことで算出する.
を次に示す最適化問題を解くことで算出する.
一般的には, 与えられた点全てに対して式 (1) を満たす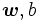 が存在するとは限らないので, 非負の変数
が存在するとは限らないので, 非負の変数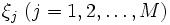 を導入し, 次の制約条件
を導入し, 次の制約条件
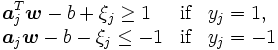
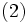
のもと,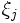 の和と
の和と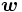 のノルムができるだけ小さくなる線形関数を考える. すなわち, 次の二次計画問題を解き
のノルムができるだけ小さくなる線形関数を考える. すなわち, 次の二次計画問題を解き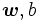 を算出する [2].
を算出する [2].
|
ここで,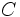 はあらかじめ設定された正の定数で,
はあらかじめ設定された正の定数で, 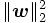 と
と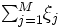 とのバランスをコントロールするパラメータである. また,
とのバランスをコントロールするパラメータである. また, 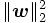 は正則化項とも呼ばれ, これを小さくすることは判別関数に用いるデータの属性を少なくし, 過学習を防ぐ役割があるとされる [6]. 問題 (3) は, 1ノルムソフトマージンSVMと呼ばれる定式化である.
は正則化項とも呼ばれ, これを小さくすることは判別関数に用いるデータの属性を少なくし, 過学習を防ぐ役割があるとされる [6]. 問題 (3) は, 1ノルムソフトマージンSVMと呼ばれる定式化である.
通常は,この問題の双対問題を考え最適化を行う [5]. 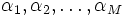 を双対変数とすれば, 問題 (3) の双対問題は
を双対変数とすれば, 問題 (3) の双対問題は
|
と書くことができ, これは1本の等式制約と各変数の上下限制約のみの凹二次関数の最大化となる. この特殊構造を用いた最適化アルゴリズム [3, 4] が知られており, データ数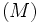 が数10万を超えるような大規模問題であっても, 高速に最適化が可能である.
が数10万を超えるような大規模問題であっても, 高速に最適化が可能である.
双対問題 (4) の最適解を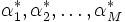 とすれば,KKT条件より主問題 (3) の最適解
とすれば,KKT条件より主問題 (3) の最適解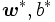 とは,
とは, 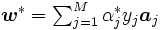 となる関係があり, さらに
となる関係があり, さらに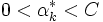 となる添え字を
となる添え字を とすれば,
とすれば, 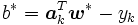 となることが示される. また, 特に添え字の集合
となることが示される. また, 特に添え字の集合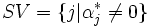 を定義すれば,
を定義すれば,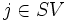 に対応するデータ
に対応するデータ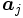 をサポート・ベクターと呼ぶ.したがって, 判別関数は双対問題の最適解とサポート・ベクターにより次のように表されることとなる.
をサポート・ベクターと呼ぶ.したがって, 判別関数は双対問題の最適解とサポート・ベクターにより次のように表されることとなる.
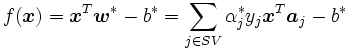
さらに, 双対問題 (4) や主問題 (3) は, サポート・ベクター以外を全て取り除いても最適解は不変であり, これらの点はSVMでの判別にはまったく寄与していないことになる.
SVMの最大の特徴は, 双対問題(4)を応用することで非線形な判別関数を構成できる点にある. 非線形な判別関数を構成するためには, まず, 適当な非線形変換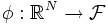 を使い各データ
を使い各データ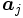 をより高い次元の特徴空間
をより高い次元の特徴空間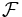 の元へと射影する. 射影された
の元へと射影する. 射影された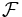 の元
の元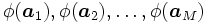 に対して,
に対して, 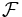 上での線形な判別関数を求めれば, 元の空間で見れば非線形な判別関数を求めたこととなる.
上での線形な判別関数を求めれば, 元の空間で見れば非線形な判別関数を求めたこととなる.
ここで, 双対問題 (4) に注目すれば,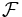 上の内積
上の内積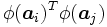 の値のみが得られれば定式化が可能であり, 特徴空間での点
の値のみが得られれば定式化が可能であり, 特徴空間での点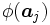 の座標を必ずしも必要としないことが分かる. そこで, SVMではカーネル関数と呼ばれる特殊な関数
の座標を必ずしも必要としないことが分かる. そこで, SVMではカーネル関数と呼ばれる特殊な関数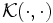 を用い元のデータ
を用い元のデータ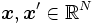 から直接
から直接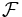 の元
の元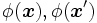 の内積
の内積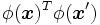 を算出し, 双対問題の最適化により非線形の判別関数が求められる [1]. よく用いられる代表的なカーネル関数として, 多項式カーネル
を算出し, 双対問題の最適化により非線形の判別関数が求められる [1]. よく用いられる代表的なカーネル関数として, 多項式カーネル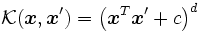 やRBFカーネル
やRBFカーネル  , (ただし
, (ただし は自然数のパラメータ,
は自然数のパラメータ, 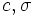 は実数のパラメータである) などがある.
は実数のパラメータである) などがある.
カーネル関数の値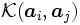 を
を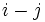 成分とする
成分とする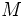 次の対称行列を
次の対称行列を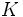 とすれば,
とすれば, 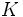 が半正定値行列となるようなカーネル関数をMercerカーネル(あるいは半正定値カーネル)と呼び, このようなカーネル関数であれば,
が半正定値行列となるようなカーネル関数をMercerカーネル(あるいは半正定値カーネル)と呼び, このようなカーネル関数であれば, となる特徴空間への変換
となる特徴空間への変換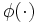 が存在することが保証される. 多項式カーネルやRBFカーネルはMercerカーネルである [5].また, Mercerカーネルを用いるのであれば, 対応した双対問題は常に凹二次関数の最大化となり, 通常の二次計画問題の解法を用いれば大域的に最適化が可能である.
が存在することが保証される. 多項式カーネルやRBFカーネルはMercerカーネルである [5].また, Mercerカーネルを用いるのであれば, 対応した双対問題は常に凹二次関数の最大化となり, 通常の二次計画問題の解法を用いれば大域的に最適化が可能である.
すなわち, 双対問題の最適解を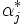 とすれば, カーネル関数を用いた場合には, 次の非線形な判別関数が求められることとなる.
とすれば, カーネル関数を用いた場合には, 次の非線形な判別関数が求められることとなる.
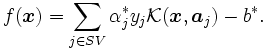
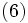
すなわち, 判別関数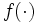 は, サポート・ベクター
は, サポート・ベクター 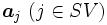 に対応するカーネル関数
に対応するカーネル関数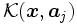 の重ね合せとして算出されると見ることができる.
の重ね合せとして算出されると見ることができる.
[1] B. E. Boser, I. M. Guyon, and V. N. Vapnik, "A training algorithm for optimal margin classifiers," in Proceedings of the fifth annual workshop on Computationa learning theory, USA, 144-152, 1992.
[2] C. Cortes and V. Vapnik, "Support-vector networks," Machine learning, 20 (1995), 273-297.
[3] T. Joachims, "Making large-scale support vector machine learning practical," in Advances in Kernel Methods, B. Schölkopf, C. Burges, and A. Smola, eds., The MIT Press, 169-184, 1999.
[4] J. C. Platt, "Fast training of support vector machines using sequential minimal optimization," in Advances in Kernel Methods, B. Schölkopf, C. Burges, and A. Smola, eds., The MIT Press, 185-208. 1999.
[5] J. Shawe-Taylor and N. Cristianini, Kernel Methods for Pattern Analysis, Cambridge University Press, 2004.
[6] V. N. Vapnik, The nature of statistical learning theory, Statistics for Engineering and Information Science, Springer-Verlag, 2000.
| 近似・知能・感覚的手法: | エキスパートシステム グラニュラーコンピューティング コア サポート・ベクター・マシーン スキーマ定理 ソフトコンピューティング タブー探索 |
サポートベクターマシン
(Support vector machine から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/07/03 03:18 UTC 版)
| 機械学習および データマイニング |
|---|
 |
| |
サポートベクターマシン(英: support-vector machine, SVM)は、教師あり学習を用いるパターン認識モデルの1つである。分類や回帰へ適用できる。1963年にウラジーミル・ヴァプニクとAlexey Ya. Chervonenkisが線形サポートベクターマシンを発表し[1]、1992年にBernhard E. Boser、Isabelle M. Guyon、ヴァプニクが非線形へと拡張した。
サポートベクターマシンは、現在知られている手法の中でも認識性能が優れた学習モデルの1つである。サポートベクターマシンが優れた認識性能を発揮することができる理由は、未学習データに対して高い識別性能を得るための工夫があるためである。
基本的な考え方
サポートベクターマシンは、線形入力素子を利用して2クラスのパターン識別器を構成する手法である。訓練サンプルから、各データ点との距離が最大となるマージン最大化超平面を求めるという基準(超平面分離定理)で線形入力素子のパラメータを学習する。
最も簡単な場合である、与えられたデータを線形に分離することが可能な(例えば、3次元のデータを2次元平面で完全に区切ることができる)場合を考えよう。
このとき、SVMは与えられた学習用サンプルを、もっとも大胆に区切る境目を学習する。学習の結果得られた超平面は、境界に最も近いサンプルとの距離(マージン)が最大となるパーセプトロン(マージン識別器)で定義される。すなわち、そのようなパーセプトロンの重みベクトル 
ニューラルネットワークを含む多くの学習アルゴリズムは、このような学習データが与えられた時
以下のような形式の ![]() カテゴリ
カテゴリ
- Support vector machineのページへのリンク