きゅうめん‐しゅうさ〔キウメンシウサ〕【球面収差】
球面収差 spherical aberration
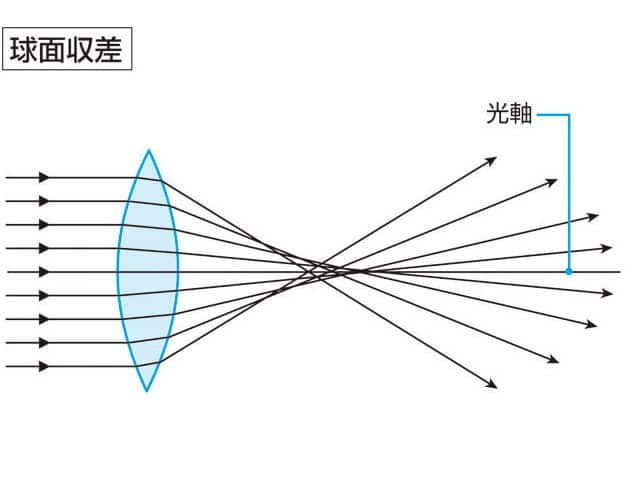
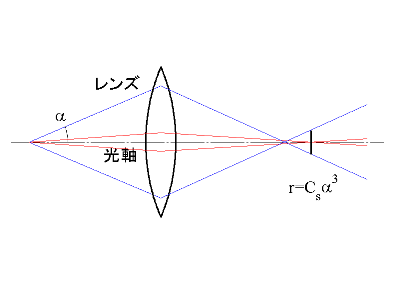
- レンズへの電子線の入射角の違いから生じる収差。光軸上の一点から出た電子線がレンズに入射するとき、理想的には光軸上の一点に集まるが、実際には大きな角度で入射したものは光軸付近のものに比べてより大きく屈折されるため、一点に集まらず拡がりを持つ。この拡がりの半径 rは、r=Csα3で表され、入射角の3乗に比例する量である。比例係数は球面収差係数(spherical aberration coefficient)と呼ばれる。球面収差を小さくするために小さな絞りを入れてレンズの中心部だけ使うと、回折収差のために点電子源の像はある大きさを持つことになり、これがSEMの分解能を決めることになる。
関連する用語
球面収差
球面収差
レンズが球面、つまり曲面で成り立っていることによって、レンズの中心から入った光と、レンズ周辺から入った光のピント位置がズレてしまうことによって起きる現象のこと。具体的には焦点移動、つまり焦点を結ぶ位置が変わってしまうことや、強い光のまわりに光のにじみ(ハロ)を生じるような現象を球面収差という。絞り込むことによってレンズ周辺から入射する光をカットできるので球面収差を取り除くことができる。また、レンズを完全な球面ではなく凹凸のある非球面レンズに仕上げることによっても、この球面収差を補正することが可能である。レンズが球面であることによって起きる収差には、狭義の球面収差のほかに、非点収差、 コマ収差 、像面湾曲、歪曲収差があり、この合計5つを発見者の名前から ザイデルの5収差 と呼ぶこともある。
球面収差
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/11/15 00:10 UTC 版)

球面収差 (きゅうめんしゅうさ、英: spherical aberration) は、球面を含む光学系において、点光源からの光線が焦点に収束せずばらつく収差をいう[1][2][3]。
コマ収差、非点収差、像面湾曲、歪曲収差と並んでザイデル収差の一つである[1][2]。
一般的に、工作機械により球面を作成することは比較的容易であるため、光学素子に球面が採用されることは多い。しかし、そのような光学系では、球面収差の影響を受け画面全体が不鮮明になる[1]。視界の中心にも影響を与えるため、望遠鏡の分解能を阻害する最大の要因である[1][2]。
写真に使う軟焦点レンズでは意図的にこれを残し印象的な像を得るのに利用している。
解決手段
光路長一定の原則を満たすと球面収差は完全に除去される[1][2]。
また、絞ると減少するが、球面収差の影響により、焦点の移動が起こる[3]。収差の影響を小さくするよう工夫されている非球面レンズ等の写真レンズであっても、球面収差の補正は完全ではないことから、十分に絞った状態での焦点距離と、開放での最良像となる距離は異なったものとなり、絞り込むにつれ最良像のできる面は移動する(一般に、「縦収差図」等と呼ばれる図で把握できる)。レンジファインダーカメラでは、どちらの距離を基準とするかはレンズ(ないしカメラ)の想定される利用状況を考慮して、設計として選択の必要があった。また、開放における最良像を求めて収差を補正するか、1段ないし2段程度絞った時の最良像を求めて収差を補正するか、という選択もあり、後者のような収差補正を「過剰補正の傾向」等という。過剰補正の傾向にあるレンズでは、開放時にはソフトフォーカス的な像となる傾向があらわれる。
屈折光学系
非球面レンズの使用で完全に除去できる[1]が、色によって屈折率が違うので、すべての色について球面収差を除去することは不可能である[1]。普通は球面をいくつか組み合わせて実用上差し支えない範囲に減少させて使用する[1]。
反射光学系
無限遠にある点光源から来る平行光線の場合放物面鏡で、焦点にある点光源から来る光線の場合楕円球面鏡で、球面収差は完全に除去される[2]。
完全に球面収差のないレンズを解析的に設計する方法

2018年に、メキシコのメキシコ国立自治大学の博士課程に在籍する大学院生ラファエル・ゴンザレスが「完全に球面収差を解消したレンズを解析的に設計する方法」を発見した[4][5][6][7]。
出典
- ^ a b c d e f g h 『天文アマチュアのための望遠鏡光学・屈折編』pp.161-202「対物レンズ」。
- ^ a b c d e 『天文アマチュアのための望遠鏡光学・反射編』pp.91-110「収差とその対策」。
- ^ a b 『ニコンの世界第6版』pp.250-255「ニッコールレンズ用語辞典」。
- ^ Gigazine(2019年7月8日)「2000年以上にわたって科学者を悩ませた「レンズの収差問題」がついに解決される」
- ^ González-Acuña, Rafael G.; Chaparro-Romo, Héctor A.. “General formula for bi-aspheric singlet lens design free of spherical aberration”. Applied Optics 57 (31): 9341-9345. doi:10.1364/AO.57.009341.
- ^ González-Acuña, Rafael G.; Julio C., Gutiérrez-Vega. “Generalization of the axicon shape: the gaxicon”. Journal of the Optical Society of America A 35 (11): 1915-1918. doi:10.1364/JOSAA.35.001915.
- ^ González-Acuña, Rafael G.; Avendaño-Alejo, Maximino; Julio C., Gutiérrez-Vega. “Singlet lens for generating aberration-free patterns on deformed surfaces”. Journal of the Optical Society of America A 36 (5): 925-929. doi:10.1364/JOSAA.36.000925.
参考文献
- 吉田正太郎『天文アマチュアのための望遠鏡光学・屈折編』誠文堂新光社、1989年。ISBN 4-416-28908-1。
- 吉田正太郎『天文アマチュアのための望遠鏡光学・反射編』誠文堂新光社、1988年。 ISBN 4-416-28813-1。
- 日本光学工業『ニコンの世界第6版』 1978年12月20日発行
球面収差
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2017/09/05 14:36 UTC 版)
光学系において点を光源とする光線が光学系を通った後、焦点1点に収束せず前後にばらつく収差。詳細は「球面収差」を参照
※この「球面収差」の解説は、「ザイデル収差」の解説の一部です。
「球面収差」を含む「ザイデル収差」の記事については、「ザイデル収差」の概要を参照ください。
「球面収差」の例文・使い方・用例・文例
球面收差と同じ種類の言葉
- 球面收差のページへのリンク