センサーの探知論
【英】:detection theory of sensor
概要
センサーの探知モデルは,「センサーの検出エネルギーの伝達系モデル」,「信号検知モデル」,「探知認識モデル」等からなるが, これらは各種のセンサー工学, 環境の物理学, 信号処理理論, 人間工学等の学際的な研究分野である. 探索理論では, これらの結果は「距離対探知確率」で出力されることを想定し, その知識に基づいて探索オペレーションにおける「目標物の発見」を定式化し, 「効率的な探索法」を解明するのが探索理論の役割である.
詳説
探索者はセンサーによって目標物の存在を検出するが, 探索理論が扱う探知探索では, 目標物の位置情報(方位及び/又は距離)を与えるセンサーが用いられる. センサーには見逃し(第1種の過誤)と虚探知 (第2種の過誤)が避けられないが, センサーの探知論では主に前者を問題にする.
目標物,環境,センサーの条件が決まればセンサーの探知能力が定まるが, センサーから同一距離にある目標物でも, 信号の短周期の変動や人間の見逃しのために探知は確率現象となる. ゆえにセンサーの瞬間的な探知能力は距離対探知確率曲線 (detection probability vs. range curve) 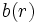 で表わされる. 通常,目標物の近傍では目標信号が強いので探知確率は高く, 遠方では低下する. またセンサーによる目標空間の走査は, 時間的に連続的な場合と離散的な場合があり, それによって探知確率
で表わされる. 通常,目標物の近傍では目標信号が強いので探知確率は高く, 遠方では低下する. またセンサーによる目標空間の走査は, 時間的に連続的な場合と離散的な場合があり, それによって探知確率 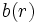 の表現が異なる. 即ち連続的な場合は探知確率密度(瞬間探知率), 離散的な場合は1回のべっ見の探知確率(べっ見探知確率) で表わされる. センサーの距離対探知確率はこれらの総称である. また距離対探知確率関数を発見法則(detection law)と呼ぶことがある. 定距離発見法則 [1] は, 探知レンジ
の表現が異なる. 即ち連続的な場合は探知確率密度(瞬間探知率), 離散的な場合は1回のべっ見の探知確率(べっ見探知確率) で表わされる. センサーの距離対探知確率はこれらの総称である. また距離対探知確率関数を発見法則(detection law)と呼ぶことがある. 定距離発見法則 [1] は, 探知レンジ 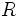 以内では確率
以内では確率  で探知し (
で探知し (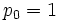 (完全定距離法則),
(完全定距離法則), 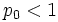 (不完全定距離法則)),
(不完全定距離法則)), 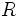 外では探知しない場合を言い, また 逆n乗発見法則(inverse
外では探知しない場合を言い, また 逆n乗発見法則(inverse  th power detection law) [2] は,
th power detection law) [2] は, 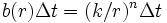 で与えられる場合を言う. 目視探索ではこの式の
で与えられる場合を言う. 目視探索ではこの式の 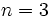 の場合逆3乗法則 (inverse cube detection law) が現実に良く合うと言われている. ただし発見法則という術語は, マクロな探索努力配分問題では目標空間上のある地点に目標物がいるとき, この点の探索努力量と目標探知確率の関係を指す言葉として使われることもある. またセンサーの有効探知距離(effective detection range) とは, 上述の距離対探知確率曲線下の面積である. ただし長レンジのセンサーでは, 目標空間の期待探索面積と等しい面積をもつ定距離センサーの探知レンジ
の場合逆3乗法則 (inverse cube detection law) が現実に良く合うと言われている. ただし発見法則という術語は, マクロな探索努力配分問題では目標空間上のある地点に目標物がいるとき, この点の探索努力量と目標探知確率の関係を指す言葉として使われることもある. またセンサーの有効探知距離(effective detection range) とは, 上述の距離対探知確率曲線下の面積である. ただし長レンジのセンサーでは, 目標空間の期待探索面積と等しい面積をもつ定距離センサーの探知レンジ 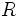 で有効探知距離を定義する場合がある.
で有効探知距離を定義する場合がある.
上述した距離対探知確率及び有効探知距離は, センサーと目標物の距離が 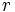 のときの瞬間的な探知能力であるが, 通常の探索では目標物や探索者は動き廻り相対距離は時々刻々変化する. 2次元空間で探索者から見た時点
のときの瞬間的な探知能力であるが, 通常の探索では目標物や探索者は動き廻り相対距離は時々刻々変化する. 2次元空間で探索者から見た時点  の目標位置を
の目標位置を 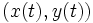 , センサーの発見法則を
, センサーの発見法則を 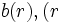 は相対距離
は相対距離 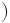 とすれば, 相対径路
とすれば, 相対径路 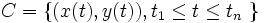 上を動く目標物の探知確率
上を動く目標物の探知確率  は, 各時点の探知の独立性を仮定すれば次式で表される.
は, 各時点の探知の独立性を仮定すれば次式で表される.
 |
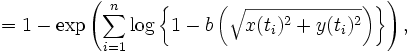 離散時点探索 離散時点探索 |
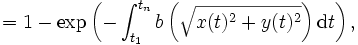 連続時間探索 連続時間探索 |
上式の指数のべきを探知ポテンシャル(sighting potential) 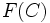 という.
という.
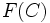 |
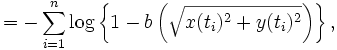 離散時点探索 離散時点探索 |
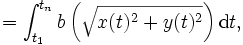 連続時間探索 連続時間探索 |
従って走査の連続性に関係なく, 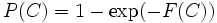 と書くことができる. また相対径路
と書くことができる. また相対径路 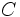 が
が  からなる場合, 上式から
からなる場合, 上式から 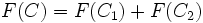 となり, 探知ポテンシャルは加法性が成り立つ. これを用いて多数の折線からなる径路上の探知や,複数の探索者による総合的な目標探知確率が求められる.
となり, 探知ポテンシャルは加法性が成り立つ. これを用いて多数の折線からなる径路上の探知や,複数の探索者による総合的な目標探知確率が求められる.
通常, センサーの探知可能距離は探索径路長に比して小さく, また目標物と探索者の変針変速は頻繁ではない. ゆえに1回の遭遇の有効(探知可能)な相対径路を直線と見なし, 横距離(最近接点距離)  を通る(無限)直線径路上を相対速度
を通る(無限)直線径路上を相対速度 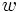 で通過する目標物を考え, その目標物に対する探知確率
で通過する目標物を考え, その目標物に対する探知確率 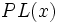 を横距離探知確率又は横距離曲線(lateral range curve)と呼ぶ. また横距離曲線下の面積(図形の尺度係数)を有効探索幅(effective sweep width)という.
を横距離探知確率又は横距離曲線(lateral range curve)と呼ぶ. また横距離曲線下の面積(図形の尺度係数)を有効探索幅(effective sweep width)という.
長レンジのセンサーでは1回の有効な遭遇径路が長いので, 目標物や探索者の変針変速やセンサーの寿命切れ, 探索条件の時間変化等のために横距離曲線は適用できない. その場合は目標物の1回の暴露状態(目標条件やその継続時間,針路,速度等)を定義し, 相対距離 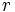 の点で暴露状態をとる目標物に対する暴露目標探知確率(exposure detection probability)
の点で暴露状態をとる目標物に対する暴露目標探知確率(exposure detection probability) 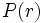 を考える. またこのときの有効探索幅は
を考える. またこのときの有効探索幅は 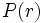 に対する完全定距離法則換算の有効探知距離で表す. 前述の距離対探知確率や有効探知距離が瞬間的な探知能力を表すのに対して, 横距離探知確率や有効探索幅, 暴露目標探知確率は,1回の遭遇のセンサー探知能力を示す.
に対する完全定距離法則換算の有効探知距離で表す. 前述の距離対探知確率や有効探知距離が瞬間的な探知能力を表すのに対して, 横距離探知確率や有効探索幅, 暴露目標探知確率は,1回の遭遇のセンサー探知能力を示す.
上述のセンサー探知能力は, 探索の場では必ずしも探索者の探索能力を表さない. 同一センサーを搭載した高速と低速のビークルでは, 高速のビークルの方が探索能力が大きいからである. このように探索者の運動力を考慮した探索システムの能力を示す尺度として, 有効探索率(effective sweep rate)が用いられる. この量は探索者が単位時間に目標空間を走査する期待面積で定義される.
これまではセンサー及び探索システムの能力の定量的表現を述べたが, 探索の濃密さを表す尺度として, カバレッジファクター(coverage factor)が用いられる. この量は探索期間中の目標空間内の延べ探索面積の期待値を, 目標存在領域の面積で除した値で定義される. 即ち目標存在領域を重複なくしらみつぶしに探したとすれば, 何回探したことになるかを表す値である. ここでは探索径路, 目標物の行動等の要因を無視しているので, 特殊な場合を除き探索オペレーションの評価尺度の目標探知確率等と直接結びつけることはできないが, カバレッジファクターが増加すれば目標探知確率は増加する.
センサーはシステム・ノイズ等のために虚探知が避けられない. この特性は虚探知率で表されるが, これは探知認識の段階で探索者が単位時間(又は1回のべっ見)当りに虚探知を起す確率を示す. センサー工学の分野では信号検知レベルの誤りの確率を誤警報率という. 虚探知のある探索では広域探索によって目標情報(コンタクトという)を得た後, コンタクトの真偽確認のために精査(目標識別という)を行う2段階探索が行われる.
[1] B. O. Koopman, Search and Screening, OEG Report No.56, 1946.
[2] K. Iida, "Inverse Nth Power Detection Law for Washburn's Lateral Range Curve," Journal of the Operations Research Society of Japan, 36 (1993), 90-101.
| 探索理論: | インスペクションゲーム カバレッジファクター クープマン問題 センサーの探知論 デイタム情報 デイタム探索 デイタム時刻 |
- センサーの探知論のページへのリンク
