第 2 種の過誤 type II error
第 2 種の過誤
“帰無仮説 H0 が誤っているにもかかわらず，H0 を採択してしまう誤り”を 第 2 種の過誤 と呼び，β で表される。
- 片側検定の場合 を図 4，図 5 に示す。
図 4 は θ0 と θ の大小関係と 棄却域（検定統計量がその範囲の値をとったときに帰無仮説が棄却されるような領域）のある方向が一致したとき， 図 5 は一致しなかったときである。図 5 のようなことは，新薬は旧薬より有効であるという作業仮説が全く誤っていた場合に相当するが， このようなことは通常はめったに起こり得ないし，あってはならないことである。しかし，万一のことを考えて， 両側検定を行えばこのような悲劇的な状況は避けることができる。
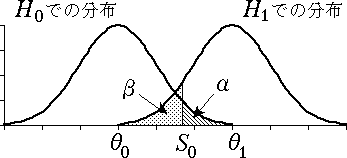
図 4．片側検定の場合の第 2 種の過誤（θ0 ＜ θ1）
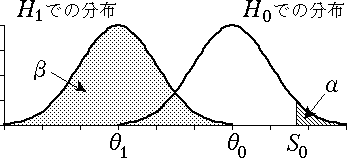
図 5．片側検定の場合の第 2 種の過誤（θ0 ＞ θ1）
- 両側検定の場合 を図 6，図 7 に示す。
θ0 ＜ θ1，θ1 ＜ θ0 のいずれの場合にも β はあまり大きくはならない。 つまり，母数 θ の全変域を考えた両側検定においては片側検定のときのような破滅的な状況は生じない。
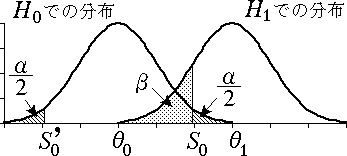
図 6．両側検定の場合の第 2 種の過誤（θ0 ＜ θ1）
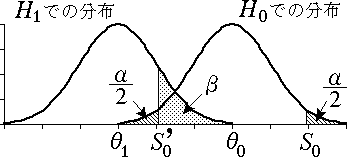
図 7．両側検定の場合の第 2 種の過誤（θ0 ＞ θ1）
しかし，そうだからといって両側検定を用いると，H0 が誤っている場合にも H0 を棄却できる確率が低くなるという問題が生ずる。 図 8 にその状況を示す。S0 という統計量が得られても，片側検定では H0 を棄却できるが両側検定では棄却できない。検出力の項を参照のこと。
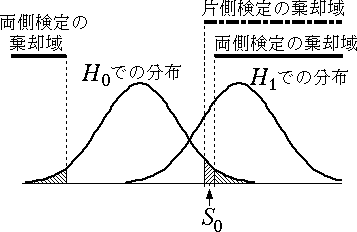 図 8．片側検定と両側検定の棄却域 |
|---|
「第 2 種の過誤」の例文・使い方・用例・文例
- 「happy」という語ではアクセントは第1音節にある
- 第１幕の終わりで状況は逆転した
- それは彼女次第だよ．なんといっても彼女がそれの所有者なんだから
- 議題の第二事項
- その作家は第二のシェークスピアと言われている
- 第１条
- 第74回アカデミー賞
- では第３章からきょうの授業を始めましょう
- ぼくは行けないよ．第一気分がよくないし，その上お金もあまりない
- 第三エンジンの点火
- 次第に彼女は私の真意を理解するだろう
- 彼女は第49回アカデミー主演女優賞を勝ち取った
- 第1章
- その学校は第2志望の学校だった
- 契約書の第3条には承服できません
- 私の母はいつも父第一だった
- 登山するときは天候をまず第一に考慮に入れなければならない
- 日本は世界第２の経済大国と信じられている
- 第二次世界大戦後の暗い日々
- 第一級殺人
Weblio日本語例文用例辞書はプログラムで機械的に例文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。
- 第2種の過誤のページへのリンク
