確率の基本的性質と定理

統計学用語辞典

確率の基本的性質と定理

　要素の個数が有限個の集合のことを有限集合 という。
　一般に，有限集合 A に属する要素の個数を n ( A ) で表すことにしよう。
　根元事象が全て同じ程度に確からしいとき，事象 A の確率を n ( A ) / n ( Ω ) で定義し，これを Pr｛A｝ と書く。
　このように確率を定義すると，明らかに次の事柄が成り立つ。

• 確率の基本的性質
  
  1. 任意の事象 A に対して，
     　　0 ≦ Pr｛A｝ ≦ 1
     特に，
     　　Pr｛Ω｝ = 1，　Pr｛φ｝ = 0
     
  2. 事象 A の余事象を とすれば，
     　　Pr｛｝ = 1 - Pr｛A｝
     

     余事象の確率

  
  
• 確率の加法定理
  
  3. 2 つの事象 A と B が互いに排反であるとき，
     　　Pr｛A ∪ B｝ = Pr｛A｝ + Pr｛B｝
     

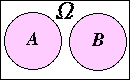
     加法定理（排反の場合）

     
     
  4. 2 つの事象 A と B について，一般に，
     　　Pr｛A ∪ B｝ = Pr｛A｝ + Pr｛B｝ - Pr｛A ∩ B｝
     

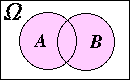
     加法定理（一般の場合）

  
  　III，IV を 確率の加法定理 と呼ぶ
  
• 確率の乗法定理
  　一般に，事象 A が起こったという条件のもとで事象 B の起こる確率を，A のもとでの B の 条件付き確率 といい，Pr｛B | A｝ で表す。ただし，Pr｛A｝ ≠ 0 とする。
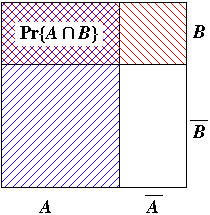
  　　Pr｛B | A｝ = n ( A ∩ B ) / n ( A ) = Pr｛A ∩ B｝ / Pr｛A｝　　…… ( 1 )
  

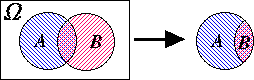
  条件付き確率

  
  
  5. 2 つの事象 A と B について，
     　　Pr｛A ∩ B｝ = Pr｛A｝ ・ Pr｛B | A｝　　…… ( 2 )
  
  V を 確率の乗法定理 という。
  
• 事象の独立・従属
  　一般に，2 つの事象 A，B があって，A が起こった場合と，起こらなかった場合とで B の起こる条件付き確率が等しいとき，事象 B は事象 A と 独立 であるという。
  　このとき，Pr｛B|A｝ = Pr｛B｝ であり，（ 3 ）式がなりたつ。（ 3 ）式は A と B について対称なので，事象 A が事象 B と独立なら，事象 B も事象 A と独立である（ A と B は 互いに独立 である ）。
  　これに対して，Pr｛B | A｝≠ Pr｛B｝ のとき，A と B は互いに 従属 である。
  
  6. 2 つの事象 A と B が互いに独立であるとき，
     　　Pr｛A ∩ B｝ = Pr｛A｝ ・ Pr｛B｝　　…… ( 3 )
     

     独立事象がともに起こる確率

  
  これは，もう一つの 確率の乗法定理 である。

例題：
　2 種類の薬剤 A，B がある。A 薬は 70% の患者に有効であり，B 薬は 60% の患者に有効である。また，A 薬，B 薬共に有効な患者は 50% であるとする。
　A 薬が無効であった患者に B 薬を投与すると何% の患者に有効となるか。
　また，B 薬が無効であった患者に A 薬を投与すると何% の患者に有効となるか。
解答：
　A 薬が有効であるという事象を A，無効であるという事象を 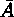とし，B 薬についても同様に B， とする。
　問題は条件付確率 Pr｛B | 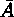｝ および Pr｛A | ｝ を求めることである。
　条件としてわかっていることは，
　　Pr｛A｝ = 0.7，　Pr｛B｝ = 0.6　および　Pr｛A ∩ B｝ = 0.5
である。
　ところ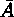で，， について
　　Pr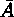｛｝ = Pr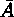｛ ∩ B｝ + Pr｛ ∩ ｝
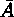　　Pr｛｝ = Pr｛A ∩ ｝ + Pr｛ ∩ ｝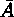
と分解することができる。ここで，
　　Pr｛ ∩ ｝
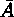　　= Pr｛｝ = 1 - Pr｛A ∪ B｝
　　= 1 - ( Pr｛A｝ + Pr｛B｝ - Pr｛A ∩ B｝)
　　= 1 - 0.7 - 0.6 + 0.5 = 0.2

となる。乗法定理の ( 1 ) 式により，
　　Pr｛B | ｝
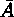　　= Pr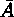｛ ∩ B｝/Pr｛｝
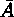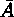　　= （ Pr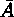｛｝ - Pr｛ ∩ ｝）/ Pr｛｝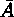
　　= { ( 1 - 0.7 ) - 0.2 } / ( 1 - 0.7 )
　　= 1 / 3
同様にして，
Pr｛A | ｝ = 1 / 2