ランデブー探索
【英】:rendezvous search
概要
友好的な2人以上の探索者が早く遭遇するための方策を 考える探索問題である. 探索者の行動領域が離散であるか連続であるか, またそれが有界であるかどうか,探索者がとり得る行動, 探索者が得る情報,探索者の数,探 索者の初期位置についての設定,探索基準等によって種々のモデルが考えられる.
詳説
夫と妻がデパートではぐれてしまったときのためにあらかじめ打ち合わせておくことにした.呼び出しサービスもなく,また2人のうち少なくとも一方が携帯電話を持っていないとしたとき2人ができるだけ早く遭遇するためにはどうしたらよいか.また,ハイカーがはぐれたときの用心のために移動方法を記したハンドブックを作成したい.再会するまでに要する時間が平均的に小さくなるような方法を求めよ.ランデブー探索(rendezvous search) とは友好的な2人以上の探索者が早く遭遇するための方策を考える探索問題である.古くから文献で指摘されてきたが,ランデブー探索の数理的研究が盛んになったのは1990年前後以降である.探索者の行動領域が離散であるか連続であるか,またそれが有界であるかどうか,探索者がとり得る行動(戦略),探索者が得る情報,探索者の数,探索者の初期位置についての設定,その他によって種々のモデルが検討され研究が続けられている.ランデブー探索では探索者をplayer と呼ぶことが多いが,一般にはランデブー探索はゲームではないことに注意すべきである.探索者が事前にお互いの役割について相談していない状況(上記ハイカーの例)を,すべての探索者が同じ戦略を用いるとしてモデル化し,この場合を(player-)symmetric という.一方探索者ごとに異なる戦略を用いることができるモデル(上記夫妻の例)をasymmetric という.他の条件が同じである場合,symmetric モデルの方がasymmetric モデルより数理的解析が困難である.探索者が2 人であるようなasymmetric モデルにおいて,探索者の一方は初期位置に留まって動かないような戦略に限定すると,他方による静止目標物の探索問題となる.探索者同士が探索領域についてどの程度の知識を共有しているか,(例えば,時計回り,方位等)もランデブー探索の重要な要素である.最小の期待再会時間をランデブー値(rendezvous value)と呼ぶ.
[直線上のランデブー探索:asymmetric モデル] 2 人の探索者(探索者I,II)が数直線上に位置している.2 人は時刻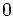 においてお互いの初期位置間の距離
においてお互いの初期位置間の距離 の確率分布
の確率分布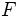 を知っているが,自分が数直線上のどこにいるのかわからない.相手が自分のどちら側にいるのか,またどちら向きに進んでいるのかを知らない.それぞれが自分の最初の向きを前進だと考える.最初に進む向きの組み合わせは4 通りあり,それぞれが確率
を知っているが,自分が数直線上のどこにいるのかわからない.相手が自分のどちら側にいるのか,またどちら向きに進んでいるのかを知らない.それぞれが自分の最初の向きを前進だと考える.最初に進む向きの組み合わせは4 通りあり,それぞれが確率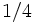 で起こる,とする. 2人は速さ
で起こる,とする. 2人は速さ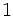 で進むことができて,できるだけ早く遭遇することを望んでいる.2 人が同時刻に同じ点にいるとき出会うことができると仮定する.期待再会時間を最小にするには2 人は直線上をどのように動けばよいか.
で進むことができて,できるだけ早く遭遇することを望んでいる.2 人が同時刻に同じ点にいるとき出会うことができると仮定する.期待再会時間を最小にするには2 人は直線上をどのように動けばよいか.
この問題において,それぞれの戦略は次の集合から選ばれる,とする.
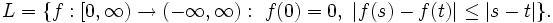
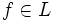 に対し,
に対し,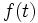 は時刻
は時刻 において,初期位置に対する探索者の相対的な位置を表す関数である,ただし探索者の最初の向きを正とする.例えば,初期位置が
において,初期位置に対する探索者の相対的な位置を表す関数である,ただし探索者の最初の向きを正とする.例えば,初期位置が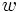 で最初の向きが左であって
で最初の向きが左であって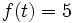 であったとする.探索者
であったとする.探索者 の時刻での位置は
の時刻での位置は である.一方,最初の向きが右であって
である.一方,最初の向きが右であって であっても時刻
であっても時刻 での位置はやはり
での位置はやはり となる.一般に,初期位置が点
となる.一般に,初期位置が点 であり戦略
であり戦略 を選んだならば,時刻
を選んだならば,時刻 での位置は確率
での位置は確率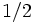 ずつで,
ずつで,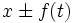 となる.
となる. 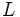 の部分集合で,傾きが
の部分集合で,傾きが (離散点を除いて)となる
(離散点を除いて)となる の全体は
の全体は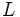 内でdense である.2 人の戦略をそれぞれ
内でdense である.2 人の戦略をそれぞれ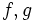 とする.探索者I,II の初期位置をそれぞれ点
とする.探索者I,II の初期位置をそれぞれ点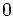 および
および とする.2 人の最初の向きが,探索者I は右,探索者II は左である,つまり
とする.2 人の最初の向きが,探索者I は右,探索者II は左である,つまり 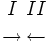 とすれば,
とすれば, 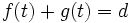 となる最小の時刻
となる最小の時刻 で2 人は出会うことになる.同様に考えて,探索者I,II の初期位置がそれぞれ点
で2 人は出会うことになる.同様に考えて,探索者I,II の初期位置がそれぞれ点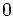 および
および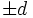 のときの2 人の期待再会時間は
のときの2 人の期待再会時間は
![T(f,g)= \int_{0}^{\infty} \frac{1}{4} \left[ \min \left\{ t: f(t)=d+g(t) \right\} + \min \left\{ t: f(t)=d- g(t) \right\}
+ \min \left\{ t:f(t)= - d+g(t) \right\} + \min \left\{t:f(t)=-d -g(t) \right\} \right] d F(d)
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/f19335ebf4ca06664201424dde41320a.png)
となる.目的はasymmetric ランデブー値 を求めること,またそれを与える戦略を見つけることである.確率分布
を求めること,またそれを与える戦略を見つけることである.確率分布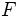 が有界で平均が
が有界で平均が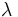 ,最大値が
,最大値が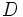 ,つまり
,つまり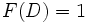 であるとする.次のような戦略の組
であるとする.次のような戦略の組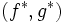 を考える.
を考える.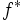 は初期位置から
は初期位置から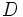 だけ進み,その後折り返して
だけ進み,その後折り返して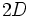 だけ進む.
だけ進む. 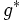 は
は 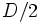 だけ進み,折り返して初期位置に戻る.次に任意の方向へ確率
だけ進み,折り返して初期位置に戻る.次に任意の方向へ確率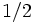 で
で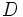 だけ進み折り返して初期位置に戻る,というものである.すると
だけ進み折り返して初期位置に戻る,というものである.すると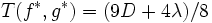 となりランデブー値
となりランデブー値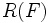 の上界が得られる.特に,初期位置間の距離
の上界が得られる.特に,初期位置間の距離 が既知の場合は
が既知の場合は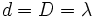 となり,ランデブー値は
となり,ランデブー値は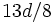 となる.このとき唯一の最適な戦略は上記
となる.このとき唯一の最適な戦略は上記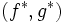 であることが知られている.
であることが知られている.
[直線上のランデブー探索:symmetric モデル] この場合は初期位置間の距離が既知であるような基本的なモデルであってもランデブー値の上界が得られているにすぎない.初期位置間の距離の分布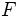 が有界であり最大値が
が有界であり最大値が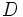 平均が
平均が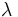 であるとする.2 人の探索者それぞれが速さ
であるとする.2 人の探索者それぞれが速さ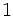 で動き,
で動き, 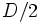 の整数倍の時刻のみに方向を変えるような戦略を次のように表現する.
の整数倍の時刻のみに方向を変えるような戦略を次のように表現する.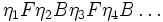 . これの意味は,まず
. これの意味は,まず 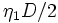 の間前進,
の間前進,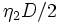 後進,....このような表現の戦略あるいはそれの組み合わせでしかもできるだけ期待再会時間を小さくするような特定の戦略を考えることが研究の現状である.例えば,
後進,....このような表現の戦略あるいはそれの組み合わせでしかもできるだけ期待再会時間を小さくするような特定の戦略を考えることが研究の現状である.例えば,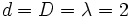 とする. 2人が
とする. 2人が ,つまり,まず確率
,つまり,まず確率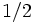 で進む向きを決め,その向きに
で進む向きを決め,その向きに だけ進み
だけ進み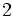 だけ戻る.再び確率
だけ戻る.再び確率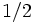 で向きを決め,同じ行動を繰り返す.この戦略での期待再会時間は
で向きを決め,同じ行動を繰り返す.この戦略での期待再会時間は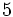 になる.より複雑な戦略を考えることにより,
になる.より複雑な戦略を考えることにより, 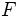 の最大値が
の最大値が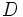 ,平均が
,平均が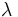 のとき現在得られている最小の上界は,
のとき現在得られている最小の上界は,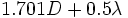 である.特に,初期位置間の距離
である.特に,初期位置間の距離 が既知の場合は
が既知の場合は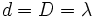 となり,ランデブー値の上界
となり,ランデブー値の上界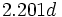 が得られる.
が得られる.
[ランデブー探索に同値な探索問題] [直線上のランデブー探索:asymmetric モデル] において,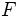 が有限の平均をもつと仮定する. 2人の戦略
が有限の平均をもつと仮定する. 2人の戦略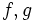 に対し,
に対し,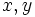 を
を
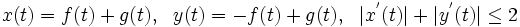
と定義する.例えば2 人の最初の向きが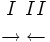 の場合,時刻
の場合,時刻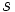 までに2 人が出会えるのは
までに2 人が出会えるのは![d \le \max_{0 \le t \le s} \left[ f(t)+g(t) \right] \,](https://cdn.weblio.jp/e7/img/dict/orjtn/01eb4d615c567ffae8d017d1c2b42f64.png) となる場合で,その確率は,
となる場合で,その確率は,![F( \max_{0 \le t \le s} \left[f(t)+g(t) \right])\,](https://cdn.weblio.jp/e7/img/dict/orjtn/770510bde09efc8e75781875034ffd2d.png) , つまり
, つまり である.他の3 つの場合も同様に考えて,結局2 人が時刻
である.他の3 つの場合も同様に考えて,結局2 人が時刻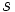 までに出会う確率は
までに出会う確率は
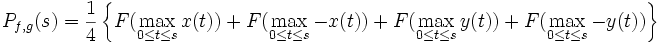
となる.一方,直線上のランデブー探索が次に述べる探索問題において戦略を上述の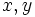 としたものに同値であることが知られている.
としたものに同値であることが知られている.
1 つの静止目標物が2 本の数直線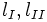 , のうちのいずれかに存在する.存在確率は
, のうちのいずれかに存在する.存在確率は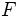 で与えられる.探索者I,II の初期位置はそれぞれ数直線,
で与えられる.探索者I,II の初期位置はそれぞれ数直線,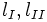 の原点である.2 人の探索者は,合計の速さが
の原点である.2 人の探索者は,合計の速さが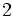 であるようにして数直線上を移動しながら目標物を探索する.2 人のうちの1 人が目標物を発見するまでの期待時間が最小になるような行動を求めよ.このとき,2 人のうちのどちらかが時刻
であるようにして数直線上を移動しながら目標物を探索する.2 人のうちの1 人が目標物を発見するまでの期待時間が最小になるような行動を求めよ.このとき,2 人のうちのどちらかが時刻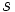 までに目標を発見する確率が
までに目標を発見する確率が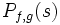 で与えられる.
で与えられる.
[3 人以上のランデブー探索] (i) 長さが である円周上に等距離
である円周上に等距離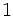 だけ離れて
だけ離れて 人の探索者がいる.円周上には位置を特定できる目印はなく,また
人の探索者がいる.円周上には位置を特定できる目印はなく,また 人のすべてにとって,どちらが時計回りかの共通の認識がない.
人のすべてにとって,どちらが時計回りかの共通の認識がない. 人が円周上で一同に会すには探索者はどのように動けばよいか.この問題のランデブー値は漸近的に
人が円周上で一同に会すには探索者はどのように動けばよいか.この問題のランデブー値は漸近的に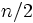 であることが知られている.(ii)
であることが知られている.(ii)  人が数直線上の連続する整数点上に位置している.それぞれが確率
人が数直線上の連続する整数点上に位置している.それぞれが確率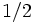 で自分の向きを決める.すべてが一同に会すことができることを確実にするのに必要な時間を最小にするにはどのように動けばよいか.この最小時間を
で自分の向きを決める.すべてが一同に会すことができることを確実にするのに必要な時間を最小にするにはどのように動けばよいか.この最小時間を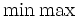 ランデブー値という.これは漸近的に
ランデブー値という.これは漸近的に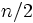 に近づくこと,さらに
に近づくこと,さらに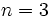 の場合は
の場合は 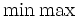 ランデブー値が
ランデブー値が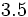 であることが知られている.
であることが知られている.
ここで紹介したモデル以外にも,例えば探索領域が2 次元以上の場合のランデブー探索,ネットワーク(あるいはグラフ)上でのランデブー探索等について論文が散見されるが,多くの問題が残されており今後の研究が待たれる状況である.ここで紹介した分析を記述した原論文についての情報も含めて,詳しくは参考文献[1] を参照されたい.
[1] S. Alpern and S. Gal, The Theory of Search Games and Rendezvous, Kluwer’s International Series, 2003.
- ランデブー探索のページへのリンク
