信頼性
【英】:reliability
概要
信頼性という用語は日常生活において自然に使用されているが, 専門用語としての定義は日本工業規格JIS Z 8115信頼性用語により定性的に次のように与えられる.「アイテムが与えられた条件で規定の期間中, 要求された機能を果たすことができる性質」. ここでアイテムとは「信頼性の対象となるシステム(系), サブシステム, 機器, 装置, 構成品, 部品, 素子, 要素などの総称またはいずれか」である.
詳説
部品, 機械の故障は日常茶飯事のことであり, 不可避なことである. 機械, システムなどの動作・故障特性について扱う分野が信頼性理論 [1, 2, 3] である. 本項においては信頼性 (reliability)について一般的に述べる. より詳しい項目は以下で解説する.
信頼性用語は日本工業規格 (JIS) により定められているので, その一部を抜粋する.
定義1 アイテム(item)とは「信頼性の対象となるシステム (系) , サブシステム, 機器, 装置, 構成品, 部品, 素子, 要素などの総称またはいずれか」である. システムとは「所定の任務を達成するために選定され, 配列され, 互いに連係して動作する一連のアイテム (ハードウェア, ソフトウェア, 人間要素) の組合せ」である.
これらの用語は上位アイテム (システム) から下位アイテム (要素) まで階層的な意味で適宜使用される.
システム (アイテム) が果たすべき仕事が任務であり, アイテム間の機能的・物理的な相互関連がインターフェースである. アイテムの周囲条件が環境である. そのとき信頼度 (reliability) は次のように定義される.
定義2 信頼度とは「アイテムが与えられた条件で規定の期間中, 要求された機能を果たす確率」である.
アイテムが規定の機能を失うことは故障であり, 故障状態の形式による分類は故障モードであり, 例えば, 断線, 短絡, 折損, 摩耗, 特性の劣化などがある.
定義3 初期故障とは「使用開始後の比較的早い時期に, 設計・製造上の欠点, 使用環境との不適合などによって起こる故障」である. 偶発故障とは「初期故障期間を過ぎ摩耗故障期間に至る以前の時期に, 偶発的に起こる故障」である. 摩耗故障とは「疲労・摩耗・老化現象などによって時間とともに故障率が大きくなる故障」である.
以下では, 確率変数  は連続形であると仮定する. 非負の
は連続形であると仮定する. 非負の  はあるアイテムの故障が起こるまでの寿命時間 (lifetime) を表す確率変数とする. 寿命分布 (lifetime distribution) を
はあるアイテムの故障が起こるまでの寿命時間 (lifetime) を表す確率変数とする. 寿命分布 (lifetime distribution) を
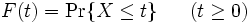
としよう. 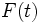 は時刻
は時刻  までに故障する確率を表す. 確率変数
までに故障する確率を表す. 確率変数  の残存確率
の残存確率
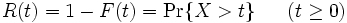
は信頼度関数とよばれる. 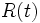 はアイテムが時刻
はアイテムが時刻  で機能している確率を表す. 確率変数
で機能している確率を表す. 確率変数  の密度は存在すると仮定し,
の密度は存在すると仮定し,
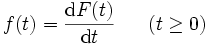
と表す. 故障率 (failure rate) あるいはハザード率 (hazard rate) は 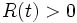 と仮定して
と仮定して
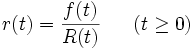
と定義される. ここで,
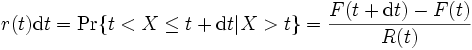
であることに注意すれば, 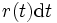 はアイテムが時刻
はアイテムが時刻  で故障していないという条件の下で, 時間区間
で故障していないという条件の下で, 時間区間 ![(t, t+{\rm d}t]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/21ef50312db2e05a3860a2c76e904821.png) で故障する条件付き確率を表す.
で故障する条件付き確率を表す.
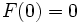 (すなわち
(すなわち 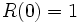 ) と仮定すると
) と仮定すると
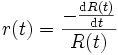
![R(t) = \exp \left[ - \int_0^t r(x) {\rm d}x \right]
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/b2031bc18cb80721a1b976648f20a6af.png)
![F(t) = 1 - \exp \left[ - \int_0^t r(x) {\rm d}x \right]
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/1b37d2c124f34d76a05afd02c01afe01.png)
![f(t) = r(t) \exp \left[ - \int_0^t r(x) {\rm d}x \right]
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/181865da848adbfc0fee822365877a2d.png)
と書くことができる. したがって, 分布, 密度関数および信頼度はいずれも故障率 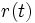 を用いて書き直すことができる. 特に,
を用いて書き直すことができる. 特に, 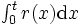 は累積ハザード関数あるいはハザード関数とよばれる.
は累積ハザード関数あるいはハザード関数とよばれる.
一般に, アイテムは時間経過とともに劣化する. この劣化する概念はエージング (aging) とよばれる. エージングは故障率の増減によって定義される.
定義4 故障率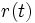 が非減少 (増加あるいは一定) 関数ならば, 寿命時間分布は,
が非減少 (増加あるいは一定) 関数ならば, 寿命時間分布は, 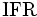 (increasing failure rate), 一定関数ならば,
(increasing failure rate), 一定関数ならば, 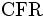 (constant failure rate), 非増加 (減少あるいは一定) 関数ならば,
(constant failure rate), 非増加 (減少あるいは一定) 関数ならば, 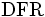 (decreasing failure rate)とよばれる.
(decreasing failure rate)とよばれる.
一般に, 確率順序 (stochastic order) は次のように定義される.
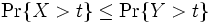
ならば,  は
は  より"確率的に小さい" (
より"確率的に小さい" (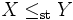 で表す) という. あるいは,
で表す) という. あるいは, 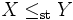 はあらゆる
はあらゆる 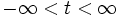 に対し,
に対し,
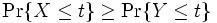
と同等である. さて, 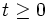 に対して
に対して ![[T - t | T > t]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/feccf87402fb5aa0e139677e31eca7d7.png) は
は 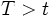 の条件の下での条件付き確率変数とする.
の条件の下での条件付き確率変数とする. 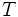 が IFR であることは, あらゆる
が IFR であることは, あらゆる 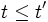 に対し,
に対し,
![[T - t | T > t] \ge_{\rm st} [T - t' | T > t']
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/6e9dc588a4931879a5175ffbf0781fce.png)
と同等である. DFR についても不等号を反対にすればよい. このようにして, エージングのより一般的な概念を確率順序によって定義できる. 詳しくは Shaked and Shanthikumar [4] 参照.
[1] R. E. Barlow and F. Proschan, Mathematical Theory of Reliability, SIAM, Philadelphia, PA, 1996.
[2] R. E. Barlow and F. Proschan, Statistical Theory of Reliability and Life Testing, To Begin With, c/o Gordon Pledger, 1142 Hornell Drive, Silver Spring, MD 20904, 1981.
[3] R. E. Barlow, Engineering Reliability, SIAM, Philadelphia, PA, 1998.
[4] M. Shaked and J. G. Shanthikumar, Reliability and Maintainability, in Stochastic Models, D. P. Heyman and M. J. Sobel, eds., North-Holland, 1990. (邦訳, 伊理・今野・刀根監訳, 「確率モデルハンドブック」, 朝倉書店).
Weblioに収録されているすべての辞書から信頼性を検索する場合は、下記のリンクをクリックしてください。
 全ての辞書から信頼性
を検索
全ての辞書から信頼性
を検索
- 信頼性のページへのリンク
