ARIMAモデル
【英】:ARIMA (autoregressive integrated moving average) model
概要
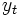 を非定常過程とし,
を非定常過程とし, を
を ,
, ,
,
 のホワイトノイズとする.
のホワイトノイズとする.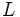 をラグ演算子
をラグ演算子 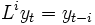 ,
, (
(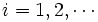 ),
),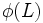 ,
, 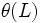 を
を 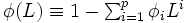 ,
,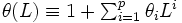 とする.
とする. を自然数として,
を自然数として, 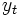 の
の  階階差
階階差 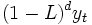 が定常な
が定常な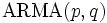 モデルで表現できるとき, モデル
モデルで表現できるとき, モデル  を次数
を次数 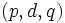 の自己回帰和分移動平均(ARIMA)モデルと呼び,
の自己回帰和分移動平均(ARIMA)モデルと呼び, 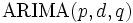 モデルと略記する.
モデルと略記する.
詳説
t を時点を表わす添字 (整数) とし,  を
を  の弱定常過程,
の弱定常過程, を
を ,
, ,
,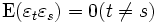 を満たすホワイトノイズ (white noise) とする.また,
を満たすホワイトノイズ (white noise) とする.また, 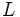 を時間を後退させる作用をもつラグ演算子 (lag operator)
を時間を後退させる作用をもつラグ演算子 (lag operator)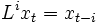 ,
,  (
(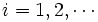 )とし,
)とし, 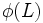 ,
, 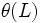 を
を 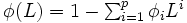 ,
,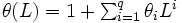 で定義される多項式ラグ演算子とする.(ただし, 多項式
で定義される多項式ラグ演算子とする.(ただし, 多項式 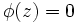 ,
, 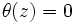 には共通根はないものとする.)
には共通根はないものとする.)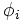 (
(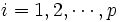 ),
), 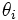 (
(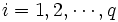 ) はパラメータ (一定) である.
) はパラメータ (一定) である.
弱定常過程  の確率的変動が
の確率的変動が 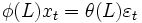 (すなわち,
(すなわち,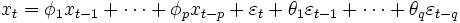 )で表わされるとき, このモデルを次数
)で表わされるとき, このモデルを次数 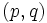 の自己回帰移動平均モデル(autoregressive moving average model) と呼び,
の自己回帰移動平均モデル(autoregressive moving average model) と呼び, 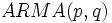 モデルと略記する.
モデルと略記する.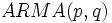 モデルが条件「
モデルが条件「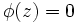 の根はすべて単位円
の根はすべて単位円 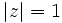 外にある」を満たせば, これを
外にある」を満たせば, これを 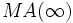 モデル :
モデル :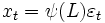 として表現出来る.(ただし
として表現出来る.(ただし 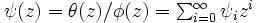 ,
,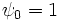 ,
,  .)また逆に条件 (反転可能性の条件 (invertibility condition) )「
.)また逆に条件 (反転可能性の条件 (invertibility condition) )「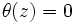 の根はすべて単位円
の根はすべて単位円 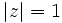 外にある」を満たせば, これを
外にある」を満たせば, これを 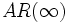 モデル :
モデル :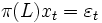 として表現出来る.(ただし
として表現出来る.(ただし 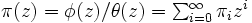 ,
, 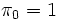 , \
, \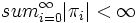 .)
.)
AR なる用語は  を自身の過去の値に回帰することに由来しており, ARモデルは理解しやすい構造を持っている.一方, MAモデルは過程の理論的性質を調べる上で重要である.また
を自身の過去の値に回帰することに由来しており, ARモデルは理解しやすい構造を持っている.一方, MAモデルは過程の理論的性質を調べる上で重要である.また 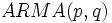 モデルは
モデルは 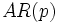 モデルと
モデルと  モデルを混合したモデルであり, これらのモデルを単独で使用した場合に比べてより少ないパラメータで定常過程の種々の性質を表現出来る点に特徴がある.
モデルを混合したモデルであり, これらのモデルを単独で使用した場合に比べてより少ないパラメータで定常過程の種々の性質を表現出来る点に特徴がある.
次に を自然数として, 次数
を自然数として, 次数  の階差演算子 (difference operator)
の階差演算子 (difference operator)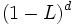 を
を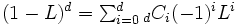 (
(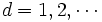 ) と定義する.非定常過程
) と定義する.非定常過程 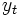 の
の  階階差
階階差  が弱定常となるとき,
が弱定常となるとき,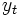 は階差次数
は階差次数  の和分モデル (integrated model) に従うと言い,このモデルを
の和分モデル (integrated model) に従うと言い,このモデルを  モデルと略記する.中でも
モデルと略記する.中でも  が特に
が特に 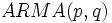 モデルに従い,
モデルに従い, と表わせるとき, このモデルを次数
と表わせるとき, このモデルを次数 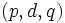 の自己回帰和分移動平均モデル (autoregressive integrated moving average model) と呼び,
の自己回帰和分移動平均モデル (autoregressive integrated moving average model) と呼び,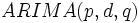 モデルと略記する.特に
モデルと略記する.特に 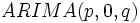 モデルが
モデルが 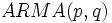 モデルに他ならない.また
モデルに他ならない.また 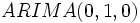 モデルはランダムウォークモデル (randomwalk model) となる.
モデルはランダムウォークモデル (randomwalk model) となる.
Box and Jenkins [2] が従来の研究成果をふまえて, ARIMAモデルの 1) 同定 (identification), 2) 推定 (estimation), 3) 診断 (diagnostic checking), 4) 予測と制御 (forecasting and control)に関する統計的分析法を体系的に提示して以来, ARIMA モデルは時系列解析に不可欠なパラメトリックモデルとして重要な役割を果たしている.
特に 1) モデルの同定に関しては, 多くの時系列において階差次数  が高々 1 (ないし 2) であることが経験的に知られている.また AR 次数
が高々 1 (ないし 2) であることが経験的に知られている.また AR 次数  , MA 次数
, MA 次数  については, 自己相関関数と偏自己相関関数の特徴をもとにこれらを決定する方法 [2] 以外に, AIC (Akaike's information criterion) 最小化法が用いられることも多い.また, 季節変動を含む経済時系列解析に有効なモデルとして, 周期
については, 自己相関関数と偏自己相関関数の特徴をもとにこれらを決定する方法 [2] 以外に, AIC (Akaike's information criterion) 最小化法が用いられることも多い.また, 季節変動を含む経済時系列解析に有効なモデルとして, 周期 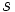 (例えば4 半期データ, 月次データに応じて
(例えば4 半期データ, 月次データに応じて 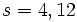 等) の季節変動を取り扱う季節的ARIMA モデル(seasonal ARIMA model) があげられる [2]. 2) パラメータの推定に関しては最尤法をはじめとした各種の非線形推定法が提案されており, 3) モデルの診断についても, 残差系列がホワイトノイズに従うか否かを残差系列の自己相関関数にもとづき検定する方法をはじめとして幾つかの統計的仮説検定法が提案されている [1], [3], [6]. 4) 予測や制御に関しては, 例えば (単純) 指数平滑化法が
等) の季節変動を取り扱う季節的ARIMA モデル(seasonal ARIMA model) があげられる [2]. 2) パラメータの推定に関しては最尤法をはじめとした各種の非線形推定法が提案されており, 3) モデルの診断についても, 残差系列がホワイトノイズに従うか否かを残差系列の自己相関関数にもとづき検定する方法をはじめとして幾つかの統計的仮説検定法が提案されている [1], [3], [6]. 4) 予測や制御に関しては, 例えば (単純) 指数平滑化法が 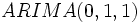 モデルの予測に最適な方法であることが明らかにされており,さらに ARIMA モデルの状態空間表現 (state space representation) やカルマンフィルター (Kalmanfilter)との関連性が明らかにされている.また ARIMA モデルは各種の需要予測や経済予測に有効なモデルであることが知られている.
モデルの予測に最適な方法であることが明らかにされており,さらに ARIMA モデルの状態空間表現 (state space representation) やカルマンフィルター (Kalmanfilter)との関連性が明らかにされている.また ARIMA モデルは各種の需要予測や経済予測に有効なモデルであることが知られている.
ARIMA モデルは様々な方向に拡張されている. 例えば金融時系列解析の分野における分散変動を考慮したARCH, GARCH, EGARCH (exponential GARCH), IGARCH (integrated GARCH) モデルや,階差次数  を実数に拡張した ARFIMA モデル (AR fractionally integratedMA model) はその一例である [3], [5].また, 計量経済モデルとの関連では,AR(I)MA モデルを多変量化した VAR(I)MA モデル (vector AR(I)MA model),外生変数 (exogenous variables) を取り入れた AR(I)MAX モデル(AR(I)MA model with exogenous variables) 等の構築や, これらをもとにしたグレンジャー因果関係 (Granger causality) の検証がなされており,さらにランダムウォークモデルとの関連で階差次数
を実数に拡張した ARFIMA モデル (AR fractionally integratedMA model) はその一例である [3], [5].また, 計量経済モデルとの関連では,AR(I)MA モデルを多変量化した VAR(I)MA モデル (vector AR(I)MA model),外生変数 (exogenous variables) を取り入れた AR(I)MAX モデル(AR(I)MA model with exogenous variables) 等の構築や, これらをもとにしたグレンジャー因果関係 (Granger causality) の検証がなされており,さらにランダムウォークモデルとの関連で階差次数 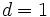 の統計的仮説検定を取り扱う単位根検定 (unit root test) や, 複数の和分モデルの一次結合が定常モデルに従う共和分モデル (cointegrated model) の構築等がなされている [4], [5], [7].
の統計的仮説検定を取り扱う単位根検定 (unit root test) や, 複数の和分モデルの一次結合が定常モデルに従う共和分モデル (cointegrated model) の構築等がなされている [4], [5], [7].
[1] T. W. Anderson, The Statistical Analysis of Time Series, John Wiley, 1971.
[2] G. E. P. Box and G. M. Jenkins, Time Series Analysis : Forecasting and Control, Holden-Day, 1970. (rev. ed., Holden-Day, 1976. 3rd ed. by G. E. P. Box, G. M. Jenkins and G. C. Reinsel, Prentice-Hall, 1994.)
[3] P. J. Brockwell and R. A. Davis, Time Series : Theory and Methods (2nd ed.), Springer-Verlag, 1991.
[4] W. A. Fuller, Introduction to Statistical Time Series (2nd ed.), John Wiley, 1996.
[5] J. D. Hamilton, Time Series Analysis, Princeton University Press, 1994.
[6] E. J. Hannan, Multiple Time Series, John Wiley, 1970.
[7] G. C. Reinsel, Elements of Multivariate Time Series Analysis (2nd ed.), Springer-Verlag, 1997.
- ありまもでる/えいあーるあいえむえいもでるのページへのリンク
