計算幾何学
【英】:computational geometry
概要
幾何学的な問題を解くための基本的なアルゴリズムの体系化をめざす学問分野. 1970年代から始まった若い分野であるが, アレンジメントやボロノイ図の計算をはじめ, すでに膨大なアルゴリズムが蓄積されている.
詳説
計算幾何学 (computational geometry) とは, 幾何的問題を効率よく解くための基本アルゴリズムの蓄積と体系化をめざす学問分野である. 計算幾何学という名称が初めて使われたのは Shamos の学位論文 [1] だと言われている. 1970年代の中頃に生まれたこの分野は, その後急速に発展し, 1980年代の中頃には相次いで標準的な教科書が出版された [2, 3, 4].
計算幾何学で扱う問題は多岐に渡るが, 以下に示すのはその中でも最も基本的なものである.
平面上に有限個の点が指定されたとき, どの点に最も近いかによって平面をそれぞれの点の勢力圏に分割した図形をボロノイ図 (Voronoi diagram) といい, 最初に与えた点を生成元という. ボロノイ図は自然界のパターンの解析, 地理的最適化など多くの応用に使われている.  個の生成元のボロノイ図は
個の生成元のボロノイ図は 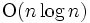 の計算量で作ることができ, これが最適であることもわかっている. ボロノイ図は, 空間の次元や距離を変えることによって多くの種類のものが定義できる. 上に述べたのはその中の最も基本的なもので, 点ボロノイ図 (Voronoi diagram for points) とよばれている.
の計算量で作ることができ, これが最適であることもわかっている. ボロノイ図は, 空間の次元や距離を変えることによって多くの種類のものが定義できる. 上に述べたのはその中の最も基本的なもので, 点ボロノイ図 (Voronoi diagram for points) とよばれている.
空間の点の集合  は, 「
は, 「 内の任意の 2 点を結ぶ線分が
内の任意の 2 点を結ぶ線分が  に含まれる」という性質を満たすとき凸集合とよばれる. 与えられた点の集合
に含まれる」という性質を満たすとき凸集合とよばれる. 与えられた点の集合  に対して,
に対して,  を含む最小の凸集合を
を含む最小の凸集合を  の凸包 (convex hull) という.
の凸包 (convex hull) という.  次元空間における
次元空間における  個の点の集合
個の点の集合  に対する凸包は,
に対する凸包は, 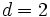 のとき
のとき 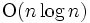 の計算量で,
の計算量で, 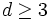 のとき
のとき 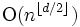 の計算量で求めることができる. ただし
の計算量で求めることができる. ただし 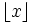 は
は  以下の最大の整数を表す. また, これより小さい計算量では求められないこともわかっている.
以下の最大の整数を表す. また, これより小さい計算量では求められないこともわかっている.
 を平面上に指定された
を平面上に指定された  個の点の集合とする.
個の点の集合とする.  の凸包の内部を,
の凸包の内部を,  に属すすべての点を頂点に使って三角形に分割した図形を,
に属すすべての点を頂点に使って三角形に分割した図形を,  を張る三角形分割 (triangulation) という.
を張る三角形分割 (triangulation) という.  を張る三角形分割は一般に何通りもある. その中で, 点ボロノイ図の双対図形として得られる三角形分割 (ドロネー図), 辺長の和が最小の三角形分割 (重み最小三角形分割) などが, 比較的ふっくらとした三角形を多く含む分割であるためによく調べられている. 前者は
を張る三角形分割は一般に何通りもある. その中で, 点ボロノイ図の双対図形として得られる三角形分割 (ドロネー図), 辺長の和が最小の三角形分割 (重み最小三角形分割) などが, 比較的ふっくらとした三角形を多く含む分割であるためによく調べられている. 前者は 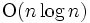 の計算量で構成できるが, 後者を構成する問題はNP困難か否かもわかっていない. 一方, 三角形の質は問わないで, どのような三角形を使ってもよいからともかく
の計算量で構成できるが, 後者を構成する問題はNP困難か否かもわかっていない. 一方, 三角形の質は問わないで, どのような三角形を使ってもよいからともかく  を張る三角形分割を作りたいという場合でも
を張る三角形分割を作りたいという場合でも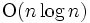 より小さい計算量では作れないことがわかっている. その意味でもドロネー図は重要な三角形分割である.
より小さい計算量では作れないことがわかっている. その意味でもドロネー図は重要な三角形分割である.
 次元空間に
次元空間に  個の超平面が与えられたとき, それらの超平面が互いに交差して空間を分割する構造はアレンジメント (arrangement) とよばれる.
個の超平面が与えられたとき, それらの超平面が互いに交差して空間を分割する構造はアレンジメント (arrangement) とよばれる. 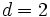 の場合は平面内の直線のアレンジメントであり, 平面を凸多角形に分割した構造である.
の場合は平面内の直線のアレンジメントであり, 平面を凸多角形に分割した構造である. 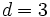 の場合は 3 次元空間内の平面のアレンジメントであり, 空間は凸多面体に分割される.
の場合は 3 次元空間内の平面のアレンジメントであり, 空間は凸多面体に分割される.
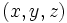 座標系をもつ3次元空間において,
座標系をもつ3次元空間において, 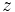 軸に平行ではない
軸に平行ではない 枚の平面が作るアレンジメントを
枚の平面が作るアレンジメントを 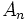 とする.
とする. 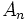 は空間をいくつかの凸多面体に分割するが, その境界となっているおのおのの凸多角形は,
は空間をいくつかの凸多面体に分割するが, その境界となっているおのおのの凸多角形は, 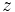 軸に平行な直線によって貫かれる順序によって,
軸に平行な直線によって貫かれる順序によって, 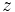 座標の大きい方から1層目, 2層目, 等と層に分類することができる. これらの階層は2次元ボロノイ図と密接な関係がある [4].
座標の大きい方から1層目, 2層目, 等と層に分類することができる. これらの階層は2次元ボロノイ図と密接な関係がある [4].
計算幾何学では, 各種幾何問題に対してそれを解く個別のアルゴリズムを追求するだけでなく, 異なる幾何構造の間の関係を調べ, それをアルゴリズムの開発に利用する努力もなされている. 異なる幾何構造をつなぐための代表的道具の一つは双対変換 (dual transformation) である. 最も素朴な双対変換は平面上の直線 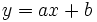 を点
を点 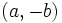 へ変換させるものである. この変換によって点は直線へ変換され, もとの平面での直線と点との接続関係は双対変換を施したあとも保たれる. このことを利用すると, たとえば平面上に指定された
へ変換させるものである. この変換によって点は直線へ変換され, もとの平面での直線と点との接続関係は双対変換を施したあとも保たれる. このことを利用すると, たとえば平面上に指定された 本の線分のすべてを通過する1本の直線を求める問題 (串刺し問題) は,
本の線分のすべてを通過する1本の直線を求める問題 (串刺し問題) は,  個のくさび形領域の共通部分を求める問題に帰着される. このように変換によって問題を扱いやすい別の問題へ帰着させる技術も計算幾何学では多数蓄積されている.
個のくさび形領域の共通部分を求める問題に帰着される. このように変換によって問題を扱いやすい別の問題へ帰着させる技術も計算幾何学では多数蓄積されている.
[1] M. I. Shamos, Computational Geometry, Ph.D. Thesis, Department of Computer Science, Yale University, New Haven, 1978.
[2] F. P. Preparata and M. I. Shamos, Computational Geometry -An Introduction, Springer-Verlag, New York, 1985.
[3] 伊理正夫監修, 腰塚武志編集, 『計算幾何学と地理情報処理』, 共立出版, 1986. (第2版, 1993).
[4] H. Edelsbrunner, Algorithms in Combinatorial Geometry, Springer-Verlag, Berlin, 1987.
計算幾何学と同じ種類の言葉
固有名詞の分類
Weblioに収録されているすべての辞書から計算幾何学を検索する場合は、下記のリンクをクリックしてください。
 全ての辞書から計算幾何学
を検索
全ての辞書から計算幾何学
を検索
- 計算幾何学のページへのリンク
