AHP
【英】:AHP (analytic hierarchy process
概要
階層化意思決定法とも訳されるが, 短くAHPと呼ばれることが多い. 複数の評価基準のもとで,多数の代替案の中からの選択, 複数の要素のすべてあるいはその一部へのリソースの配分, 複数の要素の評価や順位づけ, というタイプの決定問題のツール. 問題全体を, 究極の問題, 評価基準, 代替案という階層図に表現する. その上で, 2要素の一対比較という直感的な判断を基に, 問題全体の大局的な判断に合成する方法.
詳説
階層化意思決定法とも訳されるが, 通常AHPと呼ばれる. トマス・サーティー(Thomas L. Saaty)が, アメリカの政府機関でダンツィックらと数理計画の開発や応用をしていた経験から, トップの意思決定者が抱える構造がはっきりしなかったり複雑な問題を扱えるモデルや方法はないかと考えた上で, 開発された方法. 問題の構造を把握し難いときでも, 問題全体を, 究極の狙い, 評価基準, 代替案という階層図に表現することで明らかにした上で, 複数の評価基準のもとで, 多数の代替案の中からの選択, 複数の要素へのリソースの配分, あるいは複数の要素の評価や順位づけをする方法. 最終的には問題全体から見た代替案の重要度を求めるが, その基礎は, 2つの要素の一対比較という直感的で単純な判断の積み重ねで, これを基に問題全体の大局的な判断を支援する. 実際に組織の中だけではなく社会や公共の意思決定の場で広く実際に利用されている. [Saaty(1980, 1994), 刀根・真鍋(1990)]
[方法の概要]: AHPを用いて問題の解決を図るには, まず問題全体の構造を階層図(図1)に表す. もっとも簡単な構造は, 問題-評価基準-代替案の3層の図である. 評価基準の層の要素は互いに従属しないように選ぶ必要がある. その下に代替案を並べた層を設ける.
 |
図1:階層図 |
この階層図の上で, 最上層の問題から見た各代替案の重要度を求めて意思決定の支援をしたいのである. そのためにはまず第1層の問題から見た第2層の評価基準 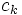 の重要度
の重要度  を求める. さらに各評価基準
を求める. さらに各評価基準 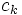 の下の代替案
の下の代替案  の(局所)重要度
の(局所)重要度  を求める. そのうえで, 代替案
を求める. そのうえで, 代替案  ごとに, 各評価基準
ごとに, 各評価基準 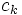 の下での重要度
の下での重要度  の, 評価基準の重要度
の, 評価基準の重要度  で重み付けをした和
で重み付けをした和  を取って, 代替案
を取って, 代替案  の(総合)重要度とする. この重要度を求める過程で一対比較評価をしている.
の(総合)重要度とする. この重要度を求める過程で一対比較評価をしている.
[一対比較から重要度の計算へ]: 例えば評価基準が4つあったらそれらを  ,
,  ,
,  ,
,  と表し, それぞれを要素と呼ぶ. 4要素あると
と表し, それぞれを要素と呼ぶ. 4要素あると  組の対があるのでそれらの対の2要素の重要さを比較判断する(一対比較する). 要素
組の対があるのでそれらの対の2要素の重要さを比較判断する(一対比較する). 要素  を要素
を要素  と比べて値
と比べて値 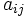 を表1に従って定め, 行列に表したもの
を表1に従って定め, 行列に表したもの ![A=[a_{ij}]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/3b0f91f83220bc69a752057adc2cc366.png) を一対比較行列と呼ぶ.
を一対比較行列と呼ぶ.
要素  が要素 が要素  に比べて に比べて |
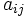 |
|
|
|
||
| 同程度に重要なとき |  |
1 |
| やや重要 |  |
3 |
| かなり重要 |  |
5 |
| 非常に重要 |  |
7 |
| 圧倒的に重要 |  |
9 |
|
|
||
| 2, 4, 6, 8 という中間値も適宜使う. | ||
 とする. とする. |
||
要素 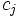 の重要度(ウエイト (weight)あるいはプライオリティ (priority)とも呼ぶ)を
の重要度(ウエイト (weight)あるいはプライオリティ (priority)とも呼ぶ)を  とすると,
とすると, 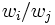 を
を 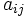 で推定していると考えられる. 行列
で推定していると考えられる. 行列 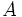 の要素
の要素 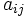 を
を 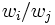 で置き換えた上でベクトル
で置き換えた上でベクトル  を右から掛けると,
を右から掛けると,
 |
 |
![\left[ \begin{array}{cccc}<br>
1 & w_1 / w_2 & w_1 / w_3 & w_1 / w_4 \\
w_2 / w_1 & 1 & w_2 / w_3 & w_2 / w_4 \\
w_3 / w_1 & w_3 / w_2 & 1 & w_3 / w_4 \\
w_4 / w_1 & w_4 / w_2 & w_4 / w_3 & 1
\end{array} \right] {\boldsymbol w}\,](https://cdn.weblio.jp/e7/img/dict/orjtn/801a588174fe846ddc642673d4a230ee.png) |
 |
![n [ w_1 \dots w_4 ] ^{\top}\,](https://cdn.weblio.jp/e7/img/dict/orjtn/bc4ff73b45c9055acb509fdf5766fc7a.png) |
で, これは固有方程式  の形をしている. 行列
の形をしている. 行列 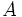 の階数は
の階数は 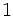 であり,
であり, 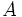 の固有値は最大固有値が
の固有値は最大固有値が  (要素数), その他のものは
(要素数), その他のものは 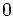 であることがいえるので,
であることがいえるので, ![A=[a_{ij}]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/3b0f91f83220bc69a752057adc2cc366.png) の最大固有値
の最大固有値  に対する固有ベクトルを
に対する固有ベクトルを  の値とする. この際に
の値とする. この際に  のすべての成分の和が
のすべての成分の和が 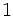 であるほうが便利なので,
であるほうが便利なので,  の成分を正規化した(各成分を
の成分を正規化した(各成分を で割った)ものを重要度とする.
で割った)ものを重要度とする.
[整合性]: 人間は一対比較で次のように整合性に欠ける判断をすることがある. (a)要素 AとBを比べるとBが好ましく, BとCを比べるとCが好ましいのに, AとCを比べるとAが好ましいとする. (b)AはBに比べて4倍程度強い, Cに比べると5倍くらい強いと判断したのに, BはCの7倍強いとする. もし整合性が完全にあれば, 3つの要素  の間で
の間で が成り立つはずである. 実際に整合性が完全にあると一対比較行列の最大固有値が要素の数に一致する(
が成り立つはずである. 実際に整合性が完全にあると一対比較行列の最大固有値が要素の数に一致する(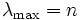 )のでそのずれを
)のでそのずれを の大きさによらぬようにした
の大きさによらぬようにした 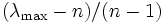 を整合度とする.この値が
を整合度とする.この値が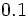 を超えると整合性が欠けることが強いので, 判断を再検討するなりやり直す必要があるとされている.
を超えると整合性が欠けることが強いので, 判断を再検討するなりやり直す必要があるとされている.
また, 一対比較の結果に使われる数値をランダムに配置した同じサイズの多数の行列の整合度の平均値(ランダム整合度)に対するこの整合度の比(整合比)も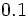 以下が好ましいとされ, 整合性の判断に用いられている.
以下が好ましいとされ, 整合性の判断に用いられている.
[ANPへ]: AHPでは階層図の各層の要素の間には従属性がないものとしている. しかし実際には, 層の中の要素の間どころか, 上下の層の要素の間にも従属性が強い場合もある. そこまで拡張すると問題のモデルは階層図ではなくネットワークになってくるので, その分野はANP(Analytic Network Process)と呼ばれている. 特に1990年前後からそのようなモデルの研究や応用が進んでいる[Saaty(1996), 高橋(1998)].
[AHPのソフトウエア]: 実際の意思決定にAHPを使うには, そのためのソフトウエアを使うと便利である. 階層図を書くこと, 一対比較をすることの支援, 代替案の総合重要度の計算から, 評価基準の重要度の代替案の重要度に対する感度分析をすることまで助けてくれる.
海外ではWindows用の "Expert Choice"がMS-DOS時代から数えると10回以上の改良の版を重ねて国際的にも広く使われている(アメリカExpert Choice社, 国内代理店:ディエムエス(株)が日本語版も出している). フィンランドのRaimo Hamalainenはヨーロッパの複数の国語を扱えるソフトを出している. 日本では(株)日本科学技術研修所の「ねまわしくん」がかなり普及している.
[1] T. L. Saaty, The Analytic Hierarchy Process, McGraw Hill, 1980. Reprinted as Vol. 1 of the AHP Series by RWS Publications, 1992.
[2] T. L. Saaty, Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process, Vol. VI of the AHP Series, PWS Publications, 1994.
[3] T. L. Saaty, Decision Making with Dependence and Feedback: Analytic Network Process, RWS Publications, 1996.
[4] 刀根 薫, 真鍋龍太郎編, 『AHP事例集』, 日科技連出版社, 1990.
[5] 高橋磐郎, 「講座:AHPからANPへの諸問題, I-V」, 『オペレーションズ・リサーチ』, 1998年1-5月号.
階層分析法
(A・H・P から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/07/15 01:51 UTC 版)
階層分析法(かいそうぶんせきほう)は、意思決定における問題の分析において、人間の主観的判断とシステムアプローチとの両面からこれを決定する問題解決型の意思決定手法。AHP (Analytic Hierarchy Process) とも呼ばれる。ピッツバーグ大学のThomas L. Saatyが提唱した。
階層分析法の主な工程として、「階層構造の構築」、「一対比較」、「ウェイトの計算」、「総合評価値の計算」が挙げられる。
階層構造の構築では、問題の要素を「最終目標」、「評価基準」、「代替案」の3階層に分ける。これによって、明確に問題を捉えることができる。評価基準とは、代替案を評価する際の基準となるものである。具体的には、「価格」や「大きさ」、「デザイン」が挙げられるだろう。代替案は、最終目標を達成するために必要と思われる項目のことで、例えば問題が「ゲーム機の選定」であれば、各社のゲーム機が代替案の候補に挙がることとなるであろう。
一対比較は、評価基準や代替案を全ての組み合わせにおいて比較することである。先の評価基準の例を用いると、「価格」と「大きさ」、「価格」と「デザイン」、「大きさ」と「デザイン」を比較することとなる。実際の比較には、9点法がよく用いられる。
ウェイトの計算は、先の一対比較の結果を基にしてウェイトを算出する工程である。ウェイトとは、代替案の重要度を表すものである。ウェイトを求めるためには、固有値法や幾何平均法など様々な種類の算出法が存在する。当然ながら、各算出法の結果を比較してみると微妙な誤差が生じる。
総合評価値の算出では、各代替案の最終的な総合評価値を求めて、最も優れた代替案を選出する。
現在では、AHPはANP (Analytic Network Process) などへ拡張発展されつつある。
概要

AHP(階層分析法)は複雑な状況での意思決定を行うための構造化法の1つである。この手法は、“正しい”決定を下すために使われるというよりも、決定者自身にとっての必然性や理解を最もよく反映させた決定を導き出すための手法である。
AHPは1970年代にトーマス・L・サーティ(現在、ピッツバーグ大学名誉教授)によって創始された意思決定法で、数学と心理学がベースになっている。既に広範囲にわたり研究され、現在はかなり洗練されたバージョンになっている。
AHPは包括的かつ合理的な意思決定のためのいくつもの枠組みを提供する。これから検討する問題を構造化する枠組み、問題に含まれる要素を数量化する枠組み、それら要素の評価を互いに関連づける枠組み、そして代替案として設定される解決案を問題全体の中で評価する枠組みである。AHPは世界中で、政治、ビジネス、産業、医療、教育など様々な分野の意思決定場面で利用されている。またこの手法を手軽に使うためのコンピュータ・ソフトウェアが、いくつかの企業から販売されている(訳者注:無償で利用できるものもある)。
AHPでは、まず自分達の決定問題をより具体的に下位の問題の階層へと分割する。下位に位置付けられた問題は、それぞれ独立に分析されることになる。階層を構成する要素は意思決定問題のどのような側面と関連していてもよい。例えば、有形か無形か、慎重に測定されたものか大ざっぱなものか、十分理解されたものかそうでないものかなどに関係なく、検討している意思決定に適用されうるものであればどんなものでも扱うことができる。
いったん階層が構築されれば、後は決定者が要素を2つずつ取り上げながら比較していくことで、システマティックに各要素を評価していくことになる。この比較では、決定者は要素について具体的なデータを使うこともできるが、要素間の相対的な意味や重要性について判断していくことができる。このように、客観的な情報だけでなく、主観的な人間の判断をも評価に利用するところがAHP の特徴といえる[1]。
ところでAHPは、上記のようにして得られた評価を、問題全体の中で比較できるよう数量化する。実際、階層内の各要素に対して重要度あるいは優先度が具体的な数値として得られる。この際、同一基準では計れないような要素についても、合理的かつ一貫した方法を利用して比較していくことができる。これを可能にしたところも、AHPが他の意思決定法と差別化されるところである。
最後に、各代替案に対する優先度が具体的な数値として計算される。ここで得られる数値が、始めに設定した問題を解決するための、代替案の代替案間での相対的な評価となる。この評価は問題の性質に合わせて解釈されることになる。
冒頭の図は、AHPの最終段階で得られる階層図の簡単な例である。決定者が決めた数値を基に計算された重要度が階層の各要素に記入されている。図からこの例はリーダーを選ぶという問題であり、そのために4つの評価基準が用意されたことが分かる。そしてAHPによる分析結果として、重要度が0.450のディックが最も望ましい候補者であると評価されたことが読み取れる。またそれだけでなく、ハリーの重要度が0.225であることから、ディックはハリーと比べリーダーとして2倍強く望まれていること、トムは彼らの中間的な存在であることも分かる。さらに今回の分析において評価基準として経験が最も重視され、続いて年齢、カリスマ性、学歴であること、またそれらの各重要度は0.400、0.300、0.200、0.100であることがわかる。
用途と適用例
AHP(階層分析法)は個人的な決定問題で大いに役立つが、複雑な決定問題に取り組む集団意思決定場面で大きな効果を発揮する。例えば利害関係がある場合、人間の認知や判断に頼らざるを得ない場合、さらにはその結果が長期にわたり影響を与える場合に大きな成果をあげている[2]。また意思決定に必要とされる要因が比較も数量化も難しい場合や、専門性や用語あるいは立場の違いにより集団内でのコミュニケーションが妨げられる場合などにも強い意思決定法である。
AHPの活用場面として次が挙げられる[3]。
- 選択 - 複数の代替案の中から1つの代替案を選択する。多くの場合、複数の評価基準による選択を指す。
- 順位付け - 代替案を最も望ましくないものから順に並べる。
- 優先順位付け - 各代替案に対し、代替案間での相対的な重要度を決定する。
- 資源配分 - 代替案間で資源を配分する。
- ベンチマーク - 他の組織の優れたやり方を、自分の組織のやり方と比較する。
- 品質マネジメント - 多次元からみた品質のあり方や品質改善を扱う。
複雑な意思決定場面での AHP の活用例は何千件にも達しており[4]、計画、資源配分、優先順位の設定、代替案間での選択など広範囲にわたり多くの成果が得られている[2]。これらの他にも、予測、総合的品質マネジメント、ビジネスプロセス・リエンジニアリング、品質機能展開、バランス・スコアカードでの利用がある[3]。一流企業での活用例も多く見られるが、セキュリティーやプライバシーを理由に一般には公表されていない。文献で閲覧できる活用例としては、近いところでは以下がある。
- 世界的な気候変動の影響を減らす最良の方法は何か(Fondazione Eni Enrico Mattei)[5]
- ソフトウェアシステムの総合品質の数量化(マイクロソフト株式会社)[6]
- 大学教授の選抜(Bloomsburg University of Pennsylvania)[7]
- 海外製造工場の建設場所の選定(ケンブリッジの大学)[8]
- 全国を横断する石油パイプライン運用のリスク査定(米国土木学会)[9]
- アメリカ合衆国の分水点に関する最良なマネジメント法の策定(アメリカ農務省)[4]
AHP は歴史的重要性から見た建造物評価といった、特定状況下における具体的な作業手順の立案にも活用されている[10]。バージニアのハイウェーの状態を評価することを目的としたビデオ映像による最近のプロジェクトにも活用されている。このプロジェクトでは、国会議員による予算決定に先立ち、ハイウェー技術師たちがAHPを活用して最適な事業範囲を決めている[11]。
教育と学術的研究
AHPを使うのに専門性や学術的なスキルは必要ないが、4年制大学の工学部[12]やビジネススクール(ビジネスに関する大学院)[13]など、多くの高等教育機関で重要な科目の1つとされている。
AHPは品質の分野では特に重要な科目とされ、シックスシグマ、リーン・シックスシグマ、QFD(品質機能展開) と一緒に多くの専門コースで教えられている[14][15][16]。
中国では100近い大学がAHPコースをもち、多くの博士課程の学生が研究や論文の主題としてAHPを選んでいる。これまでに900以上の中国の問題に関する論文が出版されており、ほとんどがAHP関連の論文であるような中国語の学術雑誌も出版されている[17]。
またこの分野に関心を持つ研究者や実務家を対象としたAHPの国際会議(ISAHP)が2年ごとに開催されている。2007年に開催されたバルパライソ(チリ)での大会では、90を超える論文が、アメリカ合衆国をはじめ、ドイツ、日本、チリ、マレーシア、ネパールなど19カ国から投稿された。内容も豊富で、外科医に対する報酬水準の確立というものから、戦略的技術ロードマップの策定や荒廃した国々におけるインフラ再構築まで広範囲にわたっている[18]。2001年から2007年までにISAHPで発表された論文のフルテキストは次から閲覧できる(ISAHP Proceedings)。(訳者注:2009年7月にピッツバーグ大学で第10回ISAHPが開催されている。第11回は2011年6月にソレント(イタリア)で開催されることが決定している。)
階層分析法の手順

後の節で改めて説明するが、AHPは、問題を検討する過程で意思決定者による判断結果を数学的に統合していくことになる。この判断結果は数にして数百にもなることがある。この数学的統合は手計算や電卓でもできるが、たくさんの判断結果を入力したり統合化したりするにはコンピュータを利用するのが一般的である。なおコンピュータを利用する場合でも、標準的な表計算用ソフトによる手軽な方法からカスタムソフトウェアを利用する方法まで様々ある。会議室を利用する場合などに便利な、意思決定者たちの判断結果を収集する特殊な装置もある(写真を参照のこと)。
AHP の手順は次のように要約できる:
- まず意思決定したい問題を階層によりモデル化する。この階層には、1つの総合目標、それを達成するためのいくつかの代替案、そしてそれら代替案を評価するためのいくつかの評価基準が含まれる。
- 階層に含まれる各要素について、要素間での優先度を確定する。このとき要素間での一対比較が利用される。例えば、不動産投資家達が、潜在的不動産を比較しながら、価格より場所、タイミングより価格を重視(優先)したいと判断したと考えるとよい。
- 2で得られた優先度を合成し、代替案の階層における統合的な優先度を算出する。先の例では、場所、価格、タイミングに関する投資家の判断結果を合成することで、各代替案(具体的な不動産)の統合的な優先度としてまとめることになる。
- 3で得られた判断結果の整合性を検討する。
- AHPを活用した最終結論を得たことになる[19]。
以下これらの手順について、節を改めながら詳しく説明する。
階層による問題のモデル化
階層分析法における第1段階は、検討する問題を階層を利用してモデル化することである。この段階で意思決定者達は、問題を大枠から細部へと検討していくことで問題の全体像を把握していき、それをAHPの規定に従い複数の階層で表現することになる。このように階層を構築していくことで、検討している問題やその文脈、またそれらに関するお互いの考え方や感じ方についての理解を深めていくことになる[19]。
階層の定義
階層とは、人、ものごと、考え方などを順位付けしたり、組織化するためにレベル分けしたシステムである。このシステムでは、一番上に要素が一つだけ配置され、その下に1つ以上の要素が連なって行く。階層の概念は直感的にも理解しやすいが、数学的に記述することもできる[20]。階層図は通常はピラミッドのようになるが、一番上に要素が一つだけ配置されること以外、必ずしもピラミッドの形をしている必要はない。
企業の組織なども階層で表され、責任の所在、リーダーシップの遂行、コミュニケーションの促進のために利用されている。「もの」に関する階層としてよく知られているものにパソコンがある。一番上にパソコン本体があり、その下にモニター、キーボード、マウスが配置される。
概念の世界においても、複雑な実体を詳細に表現するために階層が使われる。実際その実体をいくつかの成分に分解し、それらを順次階層に落とし込むことで構造化される。このときの階層数(訳者注:階層を構成する段の個数)は我々の認識を反映していることになる。なおこれらの手続きにおいて、各要素を全体から理解するように心がける必要がある。同レベルの要素であれ他のレベルの要素であれ、対象とする要素以外は一時的に無視することになる。このような方法により、どんな複雑な実体でも包括的に理解していくことができる。
この階層を解剖学を学ぶ医学生が使う場面で考えてみる。彼らは筋骨格系(手とそれを形成する筋肉や骨といった、組織と下位組織)、循環器系(たくさんのレベルと枝を含む)、神経系(たくさんの成分とサブシステムを含む)などについて独立に学んでいきながら、それら全ての系とその主要な下位組織を理解していく。優秀な学生であれば、細胞あるいは分子レベルに至るまでとことん分解していくであろう。このようにして最後には鳥瞰図とかなりの細部を理解することになる。しかもそれだけでなく、全体から見た細部の関係性さえも理解していることになる。階層を使うことで、彼らは解剖学の包括的な理解に至ることが分かる。
これと同じことが、我々が複雑な決定問題に取り組むときにも言える。すなわち、階層を使うことで大量の情報を統合しながら、その問題の本質を理解できる。情報を構造化しながら、全体として徐々に問題の見通しを良くしていくことができる[19]。
AHPの階層
AHP階層とは、意思決定問題を構造化によりモデル化したものである。この階層は、総合目標、それを達成するための選択肢あるいは代替案のグループ、そしてこれら代替案を総合目標に関係付ける因子あるいは評価基準のグループから構成される。評価基準は、問題の性格により、下位評価基準として下の方向に次々と分解していくことができる。
AHPの活用例に関するほとんどの出版物に、この階層図とその解説が掲載されている。この文献でも簡単なものを紹介する。より複雑なAHP階層については、書籍にまとめられたものがあるので、そちらを参照のこと[21]。
どのようなAHP階層も、検討中の問題の性格の他、意思決定者達の知識、判断、価値観、意見、必要性、希望などに依存して構築される。したがって階層を構築していく過程で、有意義な議論、十分な調査、そして新たな発見がなければならない。また階層を完成させた後であっても、新たに考えた評価基準や初めは重要とされなかった評価基準を追加することができる。同じことが代替案についても言え、追加、削除、あるいは変更しても差し支えない[19]。
ここでAHP階層についての理解を深めるために、総合目標とそれを達成するための3つの代替案、さらにそれら代替案を評価する4つの評価基準を含む意思決定問題について考えてみる。
この階層は下図のように、一番上に総合目標、一番下に3つの代替案、そしてその中間に4つの評価基準をもつダイアグラムとして描かれる。
このようなダイアグラムに描かれる1つ1つの箱は、専門的にノードと呼ばれる。またすぐ下の階層にある1つ以上のノードと結び付いているノードをそれらの親ノードと呼び、反対に親ノードに結び付いているノードを子ノードと呼ぶ。
例えばこれらの用語を下の図に適用すれば、総合目標は4つの評価基準の親であり、反対に4つの評価基準は総合目標の子であると言える。同様にして、各評価基準は3つの代替案の親になっていると言える。この階層には代替案は3つしかないが、下の図では対応する親の下にいちいち描かれていることに注意すること。

スペースを省略するために、下の図のように、各代替案に1つずつノードを割り当て、それらとそれらに適用する評価基準を複数の直線で結ぶ方法もある。見づらくならないように、さらにこれらの直線をいくつか省略したり、全く描かないこともできる。どのような図であれ、各代替案は階層の中で親ノードに結び付けられていることに注意が必要である。

階層の評価
階層が完成したら、意思決定者たちは各ノードを一対比較により評価する。この評価は後で数値尺度に変換される。評価基準は総合目標に対する重要度について一対比較される。代替案は各評価基準について、選好度について一対比較される。これらの一対比較の結果が数学的に処理され、各ノードの優先度が計算されることになる。
上述の「リーダー選び」について考えるならば、意思決定者の重要な仕事は、リーダーを選ぶために用意した評価基準の重要度を決めることであり、各評価基準に関して各候補者の重要度を決めることである。AHPは各代替案だけでなく、各評価基準にも意義あるかつ主観的な数値を割り振る。
AHPをおいてこのようなことができる手法はないと言っても過言ではない。そもそも、どの評価基準も候補者を比較するために有用な尺度を装備していなかったことに注意したい。
優先度の評価
この節では優先度について説明した後、それらを求める方法と簡単な例を紹介する。
優先度の定義と解釈
優先度とは、AHP 階層内の各ノードに結び付けられた数値のことである。 それらは、組になっているノード間での相対的な重要度を表している。
優先度は、確率のように0から1の間の絶対値になるが(ただし0にはならない)、単位や次元といったものはない。例えば優先度0.200のノードは優先度0.100のノードの2倍の重みを持ち、優先度が0.020のノードの10倍の重みをもつことになる。検討中の問題の性格により、この“重み”は重要性、選好性、可能性、または意思決定者が決める他の因子に関するものと解釈される。
優先度はそのアーキテクチャにより階層の中で配分されたものであり、それらの実体は、階層を作る過程で意思決定者により入力された情報により適宜解釈されるべきものである。なお、総合目標、評価基準、代替案の優先度は密接には関係してはいるが、それぞれ独立に考えることが必要である。
総合目標の優先度は1.000と定義する。これより代替案の優先度は常に1.000以下になる。評価基準の優先度は1つのレベルだけからなる場合はそれらの合計は1.000になるが、下位評価基準を持つような場合は複雑になる。以下、具体例により説明する。

例において同じレベルにある、総合目標、評価基準、代替案の優先度の和はどれも1.000である。
例にある優先度は、評価基準や代替案の重要度が計算される前に設定されるものであり、同レベルにある優先度は全て等しくなっている。これらの値は階層のデフォルト優先度と呼ばれる。たとえば階層にもし5番目の評価基準を追加されると評価基準のデフォルト優先度は0.200になり、代替案が2つだけになればデフォルト優先度は0.500になる。
ここで2つの新しい概念を与える。これらは階層内に2つ以上の評価基準のレベルがある場合、すなわち下位評価基準がある場合に適用されるもので、ローカルな優先度とグローバルな優先度である。各評価基準の下にいくつかの下位評価基準がある次の例により説明する。

ある親ノードに関して、姉妹関係にある子ノード間での相対的な重要度がローカルな優先度(灰色の数値)である。評価基準の組にしろ、それらの下にある姉妹関係にある評価基準の各組にしろ、ローカルな優先度の総和は1.000になる。一方、姉妹関係にある子ノードのローカルな各優先度と、それらの親ノードのグローバルな優先度を掛け合わせることで得られる優先度がグローバルな優先度(黒色の数値)である。同じレベルにある全ての下位評価基準のグローバルな優先度の総和は1.000になる。
これらの規則は以下のように書ける:
- 階層において、子ノードのグローバルな優先度の総和は、それらの親ノードのグローバルな優先度に等しい。
- 組となる子ノードのローカルな優先度の総和は1.000である。
ここまでデフォルト優先度について説明してきた。AHP(階層分析法)を進めていく過程で意思決定者が各ノードの重要度を決めていくが、そのときはこのデフォルト優先度を上書きしていくことになる。意思決定者は一対比較によりデフォルト優先度を上書きしていくことになる。
AHPへの批判
AHPは今やオペレーションズ・リサーチや経営科学の大抵の教科書で取り上げられ、多くの大学で教えられている。また論拠を重んじる組織においても幅広く使われている[3]。包括的合意は、専門的に妥当性があり実用的に有用性があるとき、それを批判する人はいない[6]。
1990年代初頭、AHPについて批評家たちと提案者たちの間の一連の討論が学術雑誌 Management Science[22][23][24][25]やThe Journal of the Operational Research Society[26][27]に掲載された。これらの討論は AHPに有利な方で落ち着いたようだ。
- 2001年にAHPの学術的批判を真っ向から反証する詳細な論文が、学術雑誌Operations Researchに掲載された[3]。
- 2008年に出版されたManagement Scienceの論文に多目的意思決定全分野における過去15年間の発展経過をレビューしたものがあるが、AHPに関する論文の数は他のどの分野よりも多く、この分野でいかに多くの発展が見られたかを示している[28]。
- 同じく2008年に、オペレーションズ・リサーチと経営科学の分野で主要とされる国際学会において、それらの分野におけるAHPの多大な影響を公式に認めた[注釈 1]。
しかし批判が完全に収まった訳ではない。1997年に出版された論文で、AHPの一対比較で利用する口頭による尺度(対 数値尺度)は構造的に不備がある可能性について検証された[29]。また同じ年に別の研究者により、AHP モデルを適用することで本来つけられるはずのない順序を誘引してしまう可能性が指摘されている[30]。2006年には、全ての代替案を同じように評価する評価基準を後から追加すると、元の代替案間での順序が変わってしまう可能性を指摘した論文が出版されている[31]。
AHPへの批判のほとんどが順位逆転と呼ばれる現象に関するものである。これについては、節を改めて説明する。
順位逆転現象
評価基準あるいは代替案の属性による代替案の順位付けは一般的な意味で意思決定理論の一部である。確かに、意思決定のプロセスにおいて、後から新しい代替案が追加されたとしても、元からある代替案間で順位変動は起こらない、すなわち順位逆転現象は起こらないということは、(AHPを含め)意思決定手法に必須の公理とも思える。
しかしこの仮定の妥当性はいささか疑わしいものがある。事実、一般的な意思決定場面において、新しい代替案を追加することで、元からある代替案間での順位変動が起こる場合がある。このような順位逆転現象は頻繁に起こる訳ではないが、この現象が起こる可能性は意思決定問題に活用される手法の、あるいは様々な決定理論における十分に論理的な含意であり、潜在的な前提であるといえる。
2000年のアメリカ合衆国大統領選挙は、順位逆転現象を理解する上での好例である。実際ラルフ・ネイダーは、民主党、共和党いずれの候補者からも劣勢にあったことから、当初は”無関係な”代替案だったといえる。ところが彼が後に共和党より民主党に投票していた人たちからのたくさんの票を獲得したことで逆転現象が起こった(訳者注:ジョージ・ブッシュ・Jrが勝利した)。ネイダーが立候補していなければ、アル・ゴアが勝っていたことは誰もが認めるところであり、いわば当初「無関係」であった彼の存在が順位逆転現象を引き起こしたと説明できる。1992年のジョージ・ブッシュの敗北にロス・ペローが与えた影響についても同様のことが言える(訳者注:ビル・クリントンが勝利した)。
順位逆転現象への対処には2つの方向性がある。1つは、評価基準が変わらないのであれば、代替案が新しく追加されようとも、元からある代替案間での順位逆転現象は絶対に起こるべきではないというもの。そしてもう1つが、妥当でない順位逆転現象がある一方で、起こるべくして起きる順位逆転現象もあることを認めるものである。AHP の最新バージョンでは、これらいずれの立場にも対応できるよう2つのモードが用意されている。どんな場合でも順位逆転現象を絶対に起こさないIdeal モードと、場合によっては順位逆転現象を認めるDistributive モードである。AHPを活用するにあたりどちらのモードを取るかは、意思決定者の立場、あるいは検討する問題の性格により決めることになる。
順位逆転現象と理想代替案については、学術雑誌Operations Research[3]で広範にわたり議論されている。またAHP の現時点での標準的テキストとされる書籍ではRank preservation and reversal という章にて扱われている[32]。なお後者には、AHPの枠組みを超えて、一般によく知られる順位逆転現象の例が掲載されている。コピー代替案あるいはそれに近い代替案を追加することにより起こる順位逆転現象、決定ルールの非推移性により起こる逆転現象、幻とおびき寄せ代替案を追加することにより起こる逆転現象、そして効用関数におけるスイッチング現象による逆転現象である。AHPの DistributiveモードとIdealモードについてもその書籍で紹介されている。
脚注
注釈
- ^ The Institute for Operations Research and the Management Sciences(INFORMS)はオペレーションズリサーチと経営科学の分野における実務家を対象とした国際学会であり、Management Scienceという学術雑誌を出版している。2008年にトーマス・L・サーティは階層分析法の発展への寄与を評されINFORMSのインパクト賞を受賞している。
出典
- ^ Saaty, Thomas L. (2008年6月). “Relative Measurement and its Generalization in Decision Making: Why Pairwise Comparisons are Central in Mathematics for the Measurement of Intangible Factors - The Analytic Hierarchy/Network Process”. RACSAM (Review of the Royal Spanish Academy of Sciences, Series A, Mathematics) 102 (2): 251–318 2010年9月28日閲覧。.
- ^ a b Bhushan, Navneet; Kanwal Rai (January 2004). Strategic Decision Making: Applying the Analytic Hierarchy Process. London: Springer-Verlag. ISBN 1-8523375-6-7
- ^ a b c d e Forman, Ernest H.; Saul I. Gass (2001-07). “The Analytical Hierarchy Process—An Exposition”. Operations Research 49 (4): 469–487. doi:10.1287/opre.49.4.469.11231.
- ^ a b de Steiguer, J.E.; Jennifer Duberstein; Vicente Lopes (October 2003). “The Analytic Hierarchy Process as a Means for Integrated Watershed Management”. In Renard, Kenneth G.. First Interagency Conference on Research on the Watersheds. Benson, Arizona: U.S. Department of Agriculture, Agricultural Research Service. pp. 736–740
- ^ Berrittella, Maria; Certa, Antonella; Enea, Mario; Zito, Pietro (January 2007). “An Analytic Hierarchy Process for the Evaluation of Transport Policies to Reduce Climate Change Impacts”. Fondazione Eni Enrico Mattei (Milano). doi:10.22004/ag.econ.10264. hdl:10419/74293. SSRN 962379.
- ^ a b McCaffrey, James (June 2005). “Test Run: The Analytic Hierarchy Process”. MSDN Magazine 2010年9月28日閲覧。.
- ^ Grandzol, John R. (August 2005). “Improving the Faculty Selection Process in Higher Education: A Case for the Analytic Hierarchy Process” (PDF). IR Applications 6 2010年9月28日閲覧。.
- ^ Atthirawong, Walailak; Bart McCarthy (September 2002). “An Application of the Analytical Hierarchy Process to International Location Decision-Making”. In Gregory, Mike. Proceedings of The 7th Annual Cambridge International Manufacturing Symposium: Restructuring Global Manufacturing. Cambridge, England: University of Cambridge. pp. 1–18
- ^ Dey, Prasanta Kumar (November 2003). “Analytic Hierarchy Process Analyzes Risk of Operating Cross-Country Petroleum Pipelines in India”. Natural Hazards Review 4 (4): 213–221. doi:10.1061/(ASCE)1527-6988(2003)4:4(213) 2010年9月28日閲覧。.
- ^ Lippert, Barbara C.; Stephen F. Weber (October 1995). “HIST 1.0; Decision Support Software for Rating Buildings by Historic Significance” (PDF). National Institute of Standards and Technology, NISTIR 5683. オリジナルの2010-05-29時点におけるアーカイブ。 2010年9月28日閲覧。.
- ^ Larson, Charles D.; Ernest H. Forman (January 2007). “Application of the Analytic Hierarchy Process to Select Project Scope for Videologging and Pavement Condition Data Collection”. 86th Annual Meeting Compendium of Papers CD-ROM. Transportation Research Board of the National Academies
- ^ Drake, P.R. (1998). “Using the Analytic Hierarchy Process in Engineering Education” (PDF). International Journal of Engineering Education 14 (3): 191–196 2010年9月28日閲覧。.
- ^ Bodin, Lawrence; Saul I. Gass (January, 2004). “Exercises for Teaching the Analytic Hierarchy Process”. INFORMS Transactions on Education 4 (2) 2010年9月28日閲覧。.
- ^ Hallowell, David L. (January 2005). “Analytical Hierarchy Process (AHP) – Getting Oriented”. iSixSigma.com 2010年9月28日閲覧。.
- ^ “Analytic Hierarchy Process (AHP)”. QFD Institute 2010年9月28日閲覧。.
- ^ “Analytical Hierarchy Process:: Overview”. TheQualityPortal.com 2010年9月28日閲覧。.
- ^ Sun, Hongkai (July 2005). Levy, Jason. ed. “AHP in China”. Proceedings of the 8th International Symposium on the Analytic Hierarchy Process (Honolulu, Hawaii). オリジナルの2011-07-16時点におけるアーカイブ。.
- ^ “Participant Names and Papers, ISAHP 2005, Honolulu, Hawaii” (2005年7月). 2010年9月28日閲覧。
- ^ a b c d Saaty, Thomas L. (1999-05-01). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-8-X
- ^ Saaty, Thomas L. (2010). Principia Mathematica Decernendi: Mathematical Principles of Decision Making. Pittsburgh, Pennsylvania: RWS Publications. ISBN 978-1-888603-10-1
- ^ Saaty, Thomas L.; Ernest H. Forman (1992). The Hierarchon: A Dictionary of Hierarchies. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-5-5
- ^ Dyer, J. S. (1990): Remarks on the Analytic Hierarchy Process. In: Management Science, 36 (3), S. 249-258.
- ^ M. V. Mikhalevic "Remarks on the Dyer-Saaty controversy" Cybernetics and Systems Analysis, Volume 30, Number 1 / January, 1994
- ^ Patrick T. Harker, Luis G. Vargas, "Reply to 'Remarks on the Analytic Hierarchy Process' by J. S. Dyer", Management Science, Vol. 36, No. 3 (Mar., 1990), pp. 269-273
- ^ Dyer, J.S. (1990b), "A clarification of ‘Remarks on the analytic hierarchy process’", Management Science, Vol. 36 No.3, pp.274-5.
- ^ Holder, R.D., Some Comment on the Analytic Hierarchy Process,The Journal of the Operational Research Society, 1990, 41, 11 1073-1076.
- ^ Thomas L. Saaty "Response to Holder's Comments on the Analytic Hierarchy Process" The Journal of the Operational Research Society, Vol. 42, No. 10 (Oct., 1991), pp. 909-914
- ^ Wallenius, Jyrki; James S. Dyer, Peter C. Fishburn; Ralph E. Steuer; Stanley Zionts; Kalyanmoy Deb (July 2008). “Multiple Criteria Decision Making, Multiattribute Utility Theory: Recent Accomplishments and What Lies Ahead”. Management Science 54 (7): 1339–1340. doi:10.1287/mnsc.1070.0838 2010年9月28日閲覧。.
- ^ Mari A. Pöyhönen, Raimo P. Hämäläinen, Ahti A. Salo "An Experiment on the Numerical Modelling of Verbal Ratio Statements" Journal of Multi-Criteria Decision Analysis, vol 6, no 1, ppg 1-10, 1997
- ^ Stan Schenkerman "Inducement of nonexistent order by the analytic hierarchy process", Decision Sciences, Spring 1997
- ^ Perez et al. "Another Potential Shortcoming of AHP" TOP: An Official Journal of the Spanish Society of Statistics and Operations Research, Volume 14, Number 1 / June, 2006, Springer Berlin/Heidelberg
- ^ Saaty, Thomas L. (2001). Fundamentals of Decision Making and Priority Theory. Pittsburgh, Pennsylvania: RWS Publications. ISBN 0-9620317-6-3
外部リンク
- AHP Overview E-Book - Overview of AHP Concepts and Application.
- An illustrated guide (pdf) - Dr. Oliver Meixner University of Wien - "Analytic Hierarchy Process", a very easy to understand summary of the mathematical theory
- Analytic Hierarchy Process (AHP) Tutorial - Dr. Kardi Teknomo AHP Tutorial using MS Excel.
- A・H・Pのページへのリンク
