双対変換
【英】:dual transformation
概要
双対変換は, 2つの対応する双対空間の間の1対1の変換で, 双対の双対は元に戻るという性質をもつ. もっとも基本となるのは, 点と超平面の間の双対変換である. その変換で代表的なものが, 極変換である. 双対変換により, 点集合の問題と超平面の問題を扱いやすい方で解くことができる. 2次元の場合, 線分を双対変換したものは, 楔型領域になる. ハフ変換, 共役関数の共役変換も双対変換である.
詳説
ORの様々な理論において,双対性は重要な役割を果たす.これは計算幾何でも同様で,特に双対性に対応する変換によって,ある問題を別のよりわかりやすい問題に変換して解くことができる.詳細については, [1, 2, 3]参照.
まず, 次元空間の2次曲面の極と極面に関する極変換について述べる.
次元空間の2次曲面の極と極面に関する極変換について述べる. 次元空間の超平面は,
次元空間の超平面は,
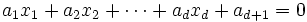
で表される. 次元空間の2次曲面は,
次元空間の2次曲面は,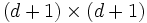 対称行列
対称行列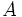 と
と 次元ベクトル
次元ベクトル  を用いて,
を用いて, 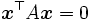 と表せる.点
と表せる.点 に対して,方程式
に対して,方程式

をみたす超平面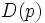 を対応させる.逆に定数ベクトル
を対応させる.逆に定数ベクトル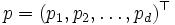 を用いて
を用いて  と書ける超平面
と書ける超平面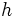 に対して点
に対して点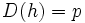 を対応させる.明らかに
を対応させる.明らかに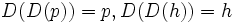 であり,この変換
であり,この変換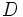 は双対変換である.点
は双対変換である.点 と超平面
と超平面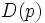 (点
(点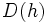 と超平面
と超平面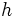 ) は,2次曲面
) は,2次曲面 に関する極と極面となる.2次曲面としては,球や面がよく用いられる.
に関する極と極面となる.2次曲面としては,球や面がよく用いられる.
以下,簡単のため2次元の場合を述べる.放物線 を用いれば,点
を用いれば,点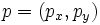 に対する極線
に対する極線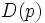 は
は となる.
となる.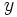 軸に平行でない直線
軸に平行でない直線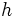 は,傾き
は,傾き と
と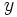 切片のマイナスの
切片のマイナスの を用いて
を用いて と表せ,
と表せ,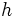 の極
の極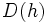 は点
は点 となる.
となる. が放物線上にあるとき,
が放物線上にあるとき, での接線が
での接線が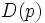 となる.
となる.
この変換は,接続関係(上下関係)を保存する.すなわち,点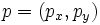 と直線
と直線 およびその双対変換
およびその双対変換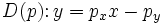 と
と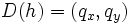 に対して
に対して と
と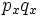 の大小関係に応じて以下のことが成立する.
の大小関係に応じて以下のことが成立する.
接続関係(上下関係)の不変性は,2次曲線として円や楕円を用いて変換を定義しても成立し,一般の 次元空間でも成立する.点の集合はそれだけで扱うとばらばらで考えにくいため,アルゴリズム的にも上下関係など関係式がわかるように,この双対変換を適用して,直線(超平面)の集合からできる平面(空間)の交差図形を利用することがしばしば行われる.このとき,双対変換で1対1に対応するとともに,この関係式が保存され,直線(超平面)が交わって空間を分割することから問題がとらえやすくなる.このような直線(超平面)による平面(空間)の交差図形をアレンジメントと呼ぶ.アレンジメントの1つのセルに対応する凸多面体についても,ファセットを含む超平面で定まる半空間の交わりとしても,端点の凸包としても表せる.これは双対性の現れで,すべての次元の構成要素であるフェイス全体がなす束でも,対応する束の上下を反転すれば同じとなる双対性が成り立つ.したがって,双対性から半空間の交わりを求めることと,点集合の凸包を求めることとは,アルゴリズムの計算量の観点からは同じである.
次元空間でも成立する.点の集合はそれだけで扱うとばらばらで考えにくいため,アルゴリズム的にも上下関係など関係式がわかるように,この双対変換を適用して,直線(超平面)の集合からできる平面(空間)の交差図形を利用することがしばしば行われる.このとき,双対変換で1対1に対応するとともに,この関係式が保存され,直線(超平面)が交わって空間を分割することから問題がとらえやすくなる.このような直線(超平面)による平面(空間)の交差図形をアレンジメントと呼ぶ.アレンジメントの1つのセルに対応する凸多面体についても,ファセットを含む超平面で定まる半空間の交わりとしても,端点の凸包としても表せる.これは双対性の現れで,すべての次元の構成要素であるフェイス全体がなす束でも,対応する束の上下を反転すれば同じとなる双対性が成り立つ.したがって,双対性から半空間の交わりを求めることと,点集合の凸包を求めることとは,アルゴリズムの計算量の観点からは同じである.
2次曲線として円を用いた場合の極変換も重要である.このとき,原点以外の点 は直線
は直線 に変換される.この直線は,原点からの距離が原点と元の点
に変換される.この直線は,原点からの距離が原点と元の点 の距離の逆数になっており,原点と元の点を結ぶ直線に垂直で,原点に関して元の点と同じ側の直線となる.
の距離の逆数になっており,原点と元の点を結ぶ直線に垂直で,原点に関して元の点と同じ側の直線となる.
円に関する極変換の変形に反転がある.反転は,原点以外の点 を上の極変換を施した直線への原点からの垂線の足に対応させる.反転により,原点を通る円は直線に変換される.この変換をもう1次元高い空間で行うと,球と平面の間の変換が得られる.たとえば、
を上の極変換を施した直線への原点からの垂線の足に対応させる.反転により,原点を通る円は直線に変換される.この変換をもう1次元高い空間で行うと,球と平面の間の変換が得られる.たとえば、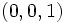 を中心とする半径1の球面を基本となる二次曲面として採用した場合の極変換では,
を中心とする半径1の球面を基本となる二次曲面として採用した場合の極変換では,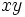 平面は
平面は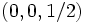 を中心とする半径
を中心とする半径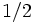 の球へ変換される.この変換は立体射影 (stereographic projection) と呼ばれる.
の球へ変換される.この変換は立体射影 (stereographic projection) と呼ばれる.
さらなる変形として,画像処理で特に用いられているハフ変換 (Hough transformation) がある.2次元の直線を原点からこの直線への垂線の距離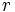 と直線と
と直線と 軸がなす角度
軸がなす角度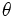 で表して,それを
で表して,それを
直線 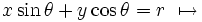 点
点 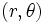
と変換する.Hough変換は,画像からの直線成分やさらには楕円などを抽出することによく用いられる.
極変換は2次曲線を核としていたが,核を一般の凸関数に拡張することもできる.この場合の双対変換は,Legendre変換と一般に呼ばれ,特に最適化の分野ではFenchelの共役性として知られている.この場合,核の凸関数の共役凸関数が定義でき,放物線 は自己共役になっている.凸関数の共役性は,凸解析の基本概念である.
は自己共役になっている.凸関数の共役性は,凸解析の基本概念である.
[1] H. Edelsbrunner, Algorithms in Combinatorial Geometry, Springer-Verlag, 1987. 邦訳(今井浩, 今井桂子訳), 『組合せ幾何学のアルゴリズム』,共立出版, 1995.
[2] F. P. Preparata and M. I. Shamos, Computational Geometry: An Introduction, Springer-Verlag, 1985. 邦訳 (浅野孝夫, 浅野哲夫訳) , 『計算幾何学入門』, 総研出版, 1992.
[3] 佐々木建昭, 今井浩, 浅野孝夫, 杉原厚吉, 『計算代数と計算幾何』, 岩波応用数学[方法9], 岩波書店, 1993.
- 双対変換のページへのリンク
 .
.
