treeとは何？わかりやすく解説 Weblio辞書

すべての辞書から再検索する

OR事典

索引トップ用語の索引ランキングカテゴリー

木

読み方：き
【英】：tree

概要

閉路を含まない連結なグラフを木という. 連結なグラフ 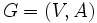$G=(V,A) \,$ に対して, $G \,$ の部分グラフであって点集合 $V \,$ をもつ木を, グラフ $G \,$ を張る木(spanning tree)といったり, グラフ $G \,$ の全域木, 極大木, 全張木あるいは, 単にグラフ $G \,$ の木などという. 根と呼ばれる 1点が指定された木を根付き木(rooted tree)という. さらに, 根付き木は, (有向グラフとして)枝の向きに沿って根からすべての点に行くことができるとき, 有向木(directed tree)と呼ばれる.

詳説

　平面上 (空間内) の幾何的な問題を解く際に対象領域を分割しながら部分領域に対応する木のノードを考えて分割の階層構造を木 (構造のデータ構造) を用いて表現する. 分割のしかたにより様々な木が得られそれぞれ特別な名前がつけられている. 計算幾何の代表的な問題である点位置決定 (point location) 問題(与えられた平面上のn点からなる直線分の平面グラフ $S\,$ に対して, 質問点 $Q\,$ が与えられたとき, $Q\,$ を含む面 (領域) を求める問題) および領域探索 (range search) 問題(与えられた平面上の $n\,$ 点の集合 $S\,$ に対して, 質問多角形 $Q\,$ が与えられたとき, $Q\,$ に含まれる $S\,$ の点を列挙する問題)を例にとり説明する.

　これらの問題は, いずれも, 与えられた対象物の集合 $S\,$ (以下台集合と呼ぶ)に対して, 質問 $Q\,$ が与えられたとき, $Q\,$ とある種の条件をみたす $S\,$ の要素を列挙する問題であり, その意味で探索問題と呼ばれている. 同一の台集合 $S\,$ に対して, 質問(問い合わせ)が繰り返し行われることも多いので, 台集合に前処理を施して質問に高速に応答できるように工夫する. すなわち, 質問に高速に応答できるように $S\,$ を計算機内で違った形(データ構造)で表現する. 実際のデータベースでもこのような工夫がなされている.

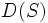　このような状況下では, $S\,$ を表現するデータ構造 $D(S)\,$ のための記憶領域, 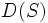$D(S)\,$ を構成するための手間(および作業領域), および質問に応答している時間 (探索時間) の 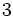$3\,$ つの基準に基づいて性能を総合的に評価しなければならない.

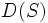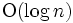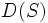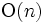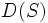　点位置決定問題に対応する 1次元の問題は, 一直線上に与えられた $n\,$ 個の点の集合 $P\,$ で分割された区間の集合 $S\,$ に対して質問点 $Q\,$ が与えられたとき $Q\,$ を含む $S\,$ の区間を求める問題となる. これは, $P\,$ および $S\,$ を平衡探索木 $D(S)\,$ で表現しておけば, $\mbox{O}(\log n)\,$ の手間で応答できる. $D(S)\,$ を構成するための手間および記憶領域はいずれも $\mbox{O}(n)\,$ である. さらに点集合に新しい点が付加されたり古い点が除去されたりして台集合 $P\,$ と $S\,$ が変化するのが普通である. このときにはそれに応じて $D(S)\,$ も更新しなければならないが, この更新操作をダイナマイゼーション (dynamization) という. 1回の更新に要する手間が 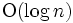$\mbox{O}(\log n)\,$ のダイナマイゼーション技術が多数知られている.

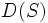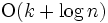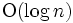　領域探索問題に対応する 1次元の問題は, 一直線上に与えられた $n\,$ 個の点の集合 $S\,$ に対して質問区間 $Q\,$ が与えられたとき $Q\,$ に含まれる $S\,$ の点をすべて列挙する問題となる. これも $S\,$ を平衡探索木 $D(S)\,$ で表現しておけば, $\mbox{O}(k+\log n)\,$ の手間で応答できる. ここで $k\,$ は列挙される点の個数である. 更新の手間も $\mbox{O}(\log n)\,$ である.

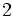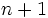　 $2\,$ 次元の点位置決定問題や領域探索問題は1次元のこのような探索問題(の系列)に帰着して解かれている. たとえば, 点位置決定問題に対して有名な手法であるスラブ法 (slab method) では, グラフの頂点を通る ( $x\,$ 軸に) 垂直な直線を引いて平面を垂直な帯に分割する. この垂直な帯がスラブ (slab) と呼ばれる. 一つのスラブ内では, 横切るグラフの線分は上下関係で一列に並べることができるのでそれを平衡探索木で表現しておく. すると, 点位置決定問題は, 質問点 $Q\,$ に対して, $Q\,$ を含むスラブを二分探索で見つける. 次にそのスラブ内で平衡探索木を利用して $Q\,$ のすぐ上にある線分を求め, その線分を境界にもつ下の面を $Q\,$ を含む領域として求めればよい. これは2次元の問題を $n+1\,$ 個のスラブでの問題(1次元の問題)に帰着していると見なせる. 応答の手間は 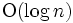$\mbox{O}(\log n)\,$ となるが, 必要とするデータ構造を構築するための手間と記憶領域は 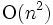$\mbox{O}(n^2)\,$ となる. これに対して, サーナクとタージャン (Sarnak-Tarjan) の残存化スラブ法 [2] では, $x\,$ 座標の値を時刻と考えて, 連続する 2つのスラブの構造の変化が定数であることに注目して, 過去に遡っても探索が可能になるようにデータ構造に工夫をしている. 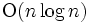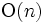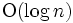これは点位置決定問題に対して, 理論的に最適なアルゴリズム (前処理時間 $\mbox{O}(n\log n)\,$ , 記憶領域 $\mbox{O}(n)\,$ , 応答時間 $\mbox{O}(\log n)\,$ ) の一つである.

　領域探索に対しては多角形は軸に平行な辺からなる長方形の場合が多く, そのときには k-d木 ( $k\,$ - $d\,$ tree), 四分木 (quadtree), 領域木 (range tree) などのデータ構造が有効である.

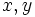　領域木は平面上の点集合の領域を $x\,$ 座標の中央値に基づいて二分割を繰り返してできる分割に対応する二分木で, 各ノードには対応する対象領域内にある点をすべて記憶しておく. すなわち区間木 (interval tree) の各ノードに対応する $x\,$ 区間に入る点を平衡探索木などで記憶しているものである. すると $x,y\,$ 軸に平行な質問長方形 $Q\,$ が与えられたとき, $Q\,$ の $x\,$ 区間が区間木の分割に対応して互いに共通部分をもたない区間の和集合として表現されるが, そのような区間に対応するノードで一次元の領域探索をすることで $Q\,$ に含まれるSの点を効率的に列挙できる.

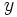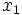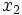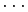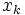　 $k\,$ - $d\,$ 木は $k\,$ 次元の空間の領域分割を表現するデータ構造の一つであり, 2次元の場合では, 根に全体領域が対応し, その左右の子には $x\,$ 座標に注目して左右に二等分された点集合の領域が対応する. 次に分割された左(右)点集合領域を $y\,$ 座標に基づいて上下に二等分しそれぞれ左(右)の子の左右の子に対応させる. 以下交互に繰り返して対応する領域に点が1個になったら分割を終了する. この分割法を表現したものが2- $d\,$ 木である. $k\,$ 次元のときは, $x_1\,$ 座標, $x_2\,$ 座標, $\cdots\,$ , $x_k\,$ 座標といってまた, 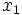$x_1\,$ 座標に戻り循環しながら分割していったものを表現する. 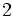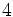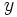これに対して, 四分木は $2\,$ 次元平面の領域分割を表現するデータ構造で, 根に全体領域が対応し, 根の $4\,$ つの子には $x\,$ 座標の中央値および $y\,$ 座標の中央値を通る水平線および垂直線をひいて四分割された部分領域が対応する. さらにそれぞれの子 $v\,$ に対応する部分領域を同様に水平線および垂直線で四等分して $v\,$ の4つの子に対応させる. このようにして得られる分割を表現するデータ構造が四分木である. 分割された領域に対象物がなくなると分割を停止する.

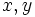　 $k\,$ - $d\,$ 木も四分木も探索は同様で, $x,y\,$ 軸に平行な質問長方形 $Q\,$ が与えられたとき, $Q\,$ と共通部分をもつ領域に対応するノードで1次元の領域探索をすることで $Q\,$ に含まれる $S\,$ の点を効率的に列挙できる.

　八分木 (octree)は3次元空間の点の集合の分割を表現するデータ構造で, 3次元の領域探索などに用いら, 2次元平面における四分木に対応する. 計算幾何の様々な探索問題に対するアルゴリズムとその詳細については文献 [1] を参照のこと.

参考文献

[1] 伊理正夫監修, 腰塚武志編集,　『計算幾何学と地理情報処理（第２版）』,　共立出版, 1993.

[2] N. Sarnak and R.E. Tarjan, "Planar Point Location Using Persistent-Search Trees," Communications of the ACM, 29 (1986), 669-679.

「OR事典」の他の用語

グラフ･ネットワーク：	最短路問題最近近傍法有向グラフ木枝点点連結度
組合せ最適化：	最小木問題最短路問題最適性の原理木板取り問題混合整数計画確率アルゴリズム
計算幾何：	最近傍グラフ最近点対最遠点対木極変換点ボロノイ図点位置決定