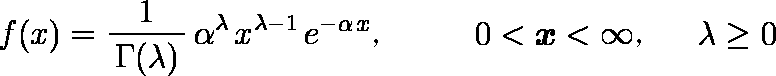ｶﾞﾝﾏ分布

統計学用語辞典

ガンマ分布

　Excel にはgammadist，gammainvという関数が用意されている。


　Γ ( λ ) はガンマ関数である。

図 1．ガンマ分布の概形

　この分布で，λ = 1 すなわち，Γ ( 1， α ) は，f ( x ) = α e ^{- α x} となり，これは指数分布である。
平均 E ( x ) ，分散 V ( x ) は
E ( x ) = λ / α，　V ( x ) = λ / α²
である。

ウィキペディア

ガンマ分布

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/11/29 10:10 UTC 版)

ガンマ分布

確率密度関数
累積分布関数
母数	$k>0$ 形状母数 $\theta >0$ 尺度母数 または、 $\lambda ={\frac {1}{\theta }}>0$ 比
台	$[0,\infty )$
確率密度関数	${\frac {1}{\Gamma (k)\,\theta ^{k}}}x^{k-1}e^{-x/\theta }={\frac {\lambda ^{k}}{\Gamma (k)}}x^{k-1}e^{-\lambda x}$
累積分布関数	${\frac {\gamma (k,x/\theta )}{\Gamma (k)}}={\frac {\gamma (k,\lambda x)}{\Gamma (k)}}$
期待値	$k\theta ={\frac {k}{\lambda }}$
中央値	単純な閉形式を持たない
最頻値	$(k-1)\theta ={\frac {k-1}{\lambda }}\ {\text{ for }}k\geqq 1$
分散	$k\theta ^{2}={\frac {k}{\lambda ^{2}}}$
歪度	${\frac {2}{\sqrt {k}}}$
尖度	${\frac {6}{k}}$
エントロピー	$k+\ln \theta +\ln \Gamma (k)+(1-k)\psi (k)$ $=k-\ln \lambda +\ln \Gamma (k)+(1-k)\psi (k)$
モーメント母関数	${\frac {1}{(1-\theta \,t)^{k}}}=\left({\frac {\lambda }{\lambda -t}}\right)^{k}$ ${\text{ for }}t<{\frac {1}{\theta }}=\lambda$
特性関数	${\frac {1}{(1-i\,\theta \,t)^{k}}}=\left({\frac {\lambda }{\lambda -it}}\right)^{k}$

確率論および統計学において、ガンマ分布 (ガンマぶんぷ、英: gamma distribution) は連続確率分布の一種である。その性質は形状母数 k、尺度母数 θ の2つの母数で特徴づけられる。主に信頼性工学における電子部品の寿命分布や通信工学におけるトラフィックの待ち時間分布に応用される。また所得分布にも応用される。

定義と性質

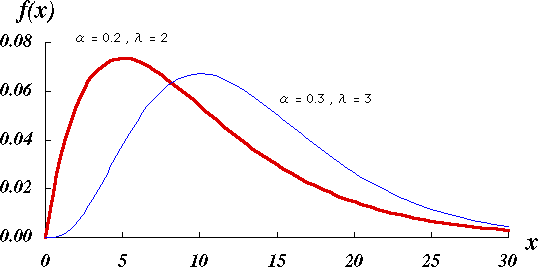
ガンマ分布は、確率密度関数が形状母数 k > 0, 尺度母数 θ > 0 を用いて

$f(x)={\frac {1}{\Gamma (k)\,\theta ^{k}}}x^{k-1}e^{-x/\theta }\ \ \ \ \mathrm {for\ } x>0$

で定義される分布である。ここで、Γ(k) はガンマ関数である。

等価な定義として、パラメータ λ = 1/θ を用いて次のように表されることもある。

$f(x)={\frac {\lambda ^{k}}{\Gamma (k)}}x^{k-1}e^{-\lambda x}\ \ \ \ \mathrm {for\ } x>0$

このとき、ガンマ分布の累積分布関数は次のように表される。

$F(x)=\int _{0}^{x}f(u)\,du={\frac {\gamma (k,x/\theta )}{\Gamma (k)}}={\frac {\gamma (k,\lambda x)}{\Gamma (k)}}$

ここで γ は不完全ガンマ関数である。

平均・分散

ガンマ分布の確率変数を X とするとき、平均 E(X) および分散 V(X) は次のように表される。

$E(X)=k\theta ={\frac {k}{\lambda }}$

$V(X)=k\theta ^{2}={\frac {k}{\lambda ^{2}}}$

特性関数

ガンマ分布の確率変数を X とするとき、特性関数 φ_X(t) は

$\phi _{X}(t)=E(e^{iXt})={\frac {1}{(1-i\,\theta \,t)^{k}}}=\left({\frac {\lambda }{\lambda -it}}\right)^{k}$

で与えられる。

これはパラメータ（平均）θ とする指数分布の特性関数を k 乗したものに一致する。このことは、特に k を整数としたときに、パラメータ θ の指数分布に従う k 個の確率変数が独立であるとき、その和が形状母数 k、尺度母数 θ のガンマ分布に従うことを表している。

再生性

ガンマ分布は再生性を有する。すなわち、パラメータに形状母数 k₁ と尺度母数 θ を持つガンマ分布の確率変数を X₁、パラメータに形状母数 k₂ と尺度母数 θ を持つガンマ分布の確率変数を X₂ とするとき、確率変数の和 X₁ + X₂ は、形状母数 k₁ + k₂、尺度母数 θ のガンマ分布に従う。

他の分布との関係

以下の分布はガンマ分布の特別な場合である。

指数分布

特に k = 1 である場合、このガンマ分布は尺度母数（平均値）を θ とする指数分布に帰着する。

アーラン分布

k が整数である場合、このガンマ分布はアーラン分布に帰着する。また、尺度母数（平均値）に θ を持つ互いに独立な n 個の指数分布の和は、パラメータに形状母数 n と尺度母数 θ を持つガンマ分布（アーラン分布）となる。

カイ二乗分布

k = n/2 (n = 1, 2, …) かつ θ = 2 である場合、ガンマ分布は自由度 n のカイ二乗分布に帰着する。

関連項目

• 確率分布
• 指数分布
• アーラン分布
• カイ二乗分布
• 逆ガンマ分布
• 一般化ガンマ分布

ウィキペディア小見出し辞書

ガンマ分布

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2019/12/01 22:40 UTC 版)

「尤度方程式」の記事における「ガンマ分布」の解説

Xi (i=1,..,n)が形状パラメータをα、尺度パラメータをβとするガンマ分布に従うとする（X ∼ Γ(α, β)）。このとき、対数尤度関数は l ( α , β , x ) = − n ln ⁡ Γ ( α ) − n α ln ⁡ β + ( α − 1 ) ∑ i = 1 n ln ⁡ x i − 1 β ∑ i = 1 n x i であり、尤度方程式は ∂ l ( α , β , x ) ∂ α = − n ψ ( α ) − n ln ⁡ β + ( α − 1 ) ∑ i = 1 n ln ⁡ x i = 0 ∂ l ( α , β , x ) ∂ β = − n α β + 1 β 2 ∑ i = 1 n x i = 0 となる。ここではψ(α)はガンマ関数の対数微分であるディガンマ関数を表す。これらを整理すると最尤推定値^β、^αが満たすべき関係式 β ^ = 1 α ^ 1 n ∑ i = 1 n x i α ^ = 1 n ∑ i = 1 n x i ( ∏ i = 1 n x i ) 1 n exp ⁡ ( ψ ( α ^ ) ) を得る。第二式を満たす^αを数値的に求めれば、第一式より^βも定まる。