クラスター分析
【英】:cluster analysis
概要
解析の対象すべてをいくつかの群に分けて, 何らかの基準にしたがって似ているものが同じ群に入るように分類する方法. 群をクラスターというが, クラスターの集合は, 対象すべてからなる集合の分割に当たる. クラスターの数と分割に対する評価基準が与えられているとき, 最適な分割を求めるのは, 組合せ最適化問題になる. 対象1個ずつの状態から, 選ばれた2つのクラスターを結合することを繰りかえす階層的方法が多数提案されている.
詳説
現象解析の基本操作の一つである分類を行う方法に関わる探索的方法論の総称がクラスター分析である. 博物学, 考古学, 生物分類学, 計量心理学など適用分野がきわめて多岐にわたることが特徴である. 欧州圏では, 自動分類法(automatic classification)と呼称することが多い. 分類操作とは, 解析の対象すべてをいくつかの群に分けて, 何らかの基準に従って似ているものが同じ群に入っているようにすることである. 群をクラスターという.
すべての対象の集合を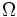 とする. これの部分集合の集合
とする. これの部分集合の集合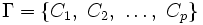 が, 次の条件を満たすとき,
が, 次の条件を満たすとき,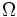 の分割という.
の分割という.
このとき, 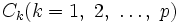 がクラスターであり,クラスター分析の目的は, 与えられた基準に従って, 最適な分割を求めることである.
がクラスターであり,クラスター分析の目的は, 与えられた基準に従って, 最適な分割を求めることである.
分類の目的によって, 分類結果, すなわち, 得られた分割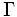 に対する評価基準が定まる. これは, 目的関数で示される. たとえば, 同じクラスターに属する対象は, お互いに類似しているほうがよいのであれば, 同じクラスターに属する2対象間の類似度の最小値を目的関数にして, それをできるだけ大きくすればよいし, 異なるクラスターに属する対象は, できるだけ類似していないほうがよければ, 異なるクラスターに属する2対象間の類似度の最大値を目的関数にして, それをできるだけ小さくすればよい.
に対する評価基準が定まる. これは, 目的関数で示される. たとえば, 同じクラスターに属する対象は, お互いに類似しているほうがよいのであれば, 同じクラスターに属する2対象間の類似度の最小値を目的関数にして, それをできるだけ大きくすればよいし, 異なるクラスターに属する対象は, できるだけ類似していないほうがよければ, 異なるクラスターに属する2対象間の類似度の最大値を目的関数にして, それをできるだけ小さくすればよい.
[分類手法]
分類方法は, いろいろ提案されているが, 大きく, 階層的分類法 (hierarchical classification) と非階層的分類法に分けられ, 階層的分類法は, さらに, 凝集型 (agglomerative type) と分枝型 (divisible type) に分けられる.
予め定めたクラスター数 に対して, 最適な分割を求める方法. 最適な分割を求めるのは, 組み合わせ最適化問題の一種であるから, 0-1変数の整数計画問題に定式化すれば, そのアルゴリズムが利用できる.
に対して, 最適な分割を求める方法. 最適な分割を求めるのは, 組み合わせ最適化問題の一種であるから, 0-1変数の整数計画問題に定式化すれば, そのアルゴリズムが利用できる.
2. 階層的分類法
クラスター数 が予め定められない場合や分類が段階的にクラスターの併合または細分によって変化することが考えられる場合には, 階層的分類が望まれる.
が予め定められない場合や分類が段階的にクラスターの併合または細分によって変化することが考えられる場合には, 階層的分類が望まれる.
対象が一つずつ分かれている状態から出発して, 最も近い二つのクラスターを併合することを繰り返して, クラスター数 を1ずつ減少させていく方法である. 予め, 二つのクラスター
を1ずつ減少させていく方法である. 予め, 二つのクラスター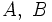 間の距離
間の距離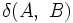 を定めておく必要がある. 手順の概要は, 次のとおりである. ここで, 対象の数を
を定めておく必要がある. 手順の概要は, 次のとおりである. ここで, 対象の数を とし,
とし,  の最終値を
の最終値を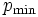 とする.
とする.
手順2. 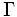 に含まれるクラスターの対の中で, 距離が最小であるものを求めて, それらを結合し,
に含まれるクラスターの対の中で, 距離が最小であるものを求めて, それらを結合し,  の値を1だけ小さくする.
の値を1だけ小さくする. 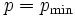 であれば, 終了する.
であれば, 終了する.
手順3. 結合してできたクラスターと他のクラスターの間の距離を計算して手順2にもどる.
クラスター間の距離の定義は, いろいろ考えられているが, 対象 と対象
と対象 の間の距離
の間の距離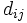 を予め定めておいて, それを用いて表すことが多い. 対象間距離は, 対象のいくつかの特性の測定値から計算される. 特性の単位がすべて揃っているときは, ユークリッド距離が使えるが, 一般には, 重み付きユークリッド距離を用いる. 類似度やアンケートの回答の一致の程度から, 距離を定めることもある. このときは, 類似度などが大きくなるほど, 距離が小さくなるようにする.
を予め定めておいて, それを用いて表すことが多い. 対象間距離は, 対象のいくつかの特性の測定値から計算される. 特性の単位がすべて揃っているときは, ユークリッド距離が使えるが, 一般には, 重み付きユークリッド距離を用いる. 類似度やアンケートの回答の一致の程度から, 距離を定めることもある. このときは, 類似度などが大きくなるほど, 距離が小さくなるようにする.
対象間距離を用いるクラスター間の距離の定義の代表的なものを挙げる.
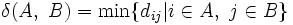
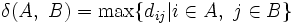
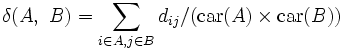
ここで, 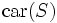 は, 集合
は, 集合 の要素数を表す. 上から順に, 最短距離, 最長距離, 群間平均距離という. 手順1で,
の要素数を表す. 上から順に, 最短距離, 最長距離, 群間平均距離という. 手順1で, 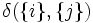 を計算しなければいけないが, 対象間距離を用いるときは,
を計算しなければいけないが, 対象間距離を用いるときは, 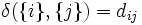 となる.
となる.
凝集型方法では, クラスター間の距離の定義によって, 分類結果が異なる可能性がある. そこで, クラスター間の距離の定義に対応して, 方法に名称が付けられている. 最短距離, 最長距離, 群間平均距離を用いるときは, それぞれ最短距離法, 最長距離法, 群間平均距離法という. 最短距離法の別名としては, 最近隣法, 単連結法などがあり, 最長距離法の別名には, 最遠隣法, 完全連結法などがある. なお, 最短距離法は, 最小木問題のクラスカル法に当たる. 多くのクラスター間の距離を統一的に表わす距離が定義されていて, それを用いる凝集型方法を組み合わせ的方法(combinatorial method)と呼んでいる [6].
凝集型方法は, ある一つの の値に対する分割を求める場合でも, 非常に少ない計算量でよい解を求めるアルゴリズムである. 一般的には, 与えられた目的関数に対して, いつも良い分割を与えるクラスター間の距離の定義は存在しないから, 定義を変えていろいろな分割を求めて, それらの中から最も良いものを選べばよいが, 異なるクラスターに属する2対象間の距離の最小値, すなわち, 最短距離を最大にする場合は, 最短距離法で常に最適解が得られる. 結合していく過程と結合する二つのクラスター間の距離は, 樹形図 (dendrogram) で示される.
の値に対する分割を求める場合でも, 非常に少ない計算量でよい解を求めるアルゴリズムである. 一般的には, 与えられた目的関数に対して, いつも良い分割を与えるクラスター間の距離の定義は存在しないから, 定義を変えていろいろな分割を求めて, それらの中から最も良いものを選べばよいが, 異なるクラスターに属する2対象間の距離の最小値, すなわち, 最短距離を最大にする場合は, 最短距離法で常に最適解が得られる. 結合していく過程と結合する二つのクラスター間の距離は, 樹形図 (dendrogram) で示される.
凝集型とは逆に, 全対象を一つのクラスターにした状態から出発して, クラスターの分割を繰り返すことにより, トップダウンに階層分類を行う. 逐次二分割方式が多いが, 三つ以上に分割できる方式もある. 時間経過とともに進化して分岐してきたものの分類には適しているが, 凝集型に比べると, はるかに計算量が増える.
[1] 奥野忠一, 久米均, 芳賀敏郎, 吉澤正, 『多変量解析法(改訂版)』, 日科技連出版, 1981.
[2] 大隅昇, L. ルバール他, 『記述的多変量解析法』, 日科技連出版社, 1994.
[3] M. R. Anderberg, Cluster Analysis for Applications, Academic Press, 1973.
[4] T. S. Arthanari and Y. Dodge, Mathematical Programming in Statistics, John-Wiley and Sons, 1981.
[5] B. Everitt, Cluster Analysis, 3rd edn., Edward Arnold, 1993.
[6] G. N. Lance and W. T. Williams, "A General Theory of Classificatory Sorting Strategies 1 - Hierarchical System," Computer Journal, 9 (1967), 373-380.
Weblioに収録されているすべての辞書からクラスター分析を検索する場合は、下記のリンクをクリックしてください。
 全ての辞書からクラスター分析
を検索
全ての辞書からクラスター分析
を検索
- クラスター分析のページへのリンク

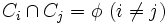
 とし,
とし, 
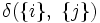 を
を