プロジェクト‐かんり〔‐クワンリ〕【プロジェクト管理】
プロジェクト管理
【英】:project management
概要
大規模な建設や研究開発などをプロジェクトと呼び, これらプロジェクトを計画・設計・日程立案・組織化し, その実行過程を統制することがプロジェクト管理である. しかし実際には, その意味するところは, その言葉を使う人によって異なる. ORの分野では伝統的に, PERT/CPMやプロジェクトの経済性分析など, 問題を解く技術的な側面に主な関心がもたれてきたが, 他の分野では, プロジェクト組織といった, 人間が関係する側面により関心が払われてきた.
詳説
大規模な建設や研究開発をプロジェクト(project)とよび, これらプロジェクトを計画・設計・日程立案・組織化し, その実行過程を統制することをプロジェクト管理という. しかし実際には, プロジェクト管理の意味するところは, その言葉を使う人によって異なる. ORの分野では伝統的に, PERT/CPMなど問題を解く技術的な側面に主な関心がもたれてきたが, ほかの分野では, プロジェクト組織といった, 人間が関係する側面により関心が払われてきた.
PERT/CPMは, プロジェクト・スケジューリング(project scheduling)と総称される. PERTは作業(job, activity)の所要時間に関して確率的取扱いを含むのに対し, CPMは決定論的アプローチである. それでも, これら2つの方法はよく似た手法であり, PERT/CPM法とよばれる [1, 2].
(1)PERT: PERTは, それまで使われてきたガントチャート(バーチャートともいう)に替わって, 大規模な工事の計画・管理の手法として, 1958年に米海軍のポラリス・ミサイル開発プロジェクトのために生み出された.
PERTでは, プロジェクトを構成する作業の先行関係を表現するのに, 矢線(arrow)と結合点(node, event)とからなる有向のネットワーク図を用い, これに基づいて日程を計画・管理する手法である. また, このネットワーク図をアローダイヤグラムや矢線図(arrow diagram)とよび, そのかき方に次の3つのルールがある.
(i)1つの作業は2つの結合点を結ぶ1つの矢線で図示し, 矢線の両端の結合点番号の対 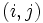 によって作業を表す(図1 (a)参照).
によって作業を表す(図1 (a)参照).
(ii)「作業Cは作業AとBがすむと取りかかることができる」という先行関係は, 図1(b)のように表現する. 作業の先行関係を正確に表現するためにダミー作業が使われる(図1 (c)参照).
(iii)付番を一意的とするため, 平行作業には図1 (d)のようにダミー作業を導入する.
 |
図1 作業と先行関係の表現法 |
アローダイヤグラムの例を図2に示す.
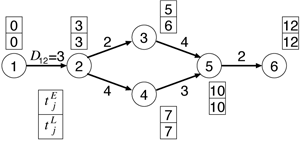 |
図2 アローダイヤグラムと結合点時刻の例 |
作業  の作業時間
の作業時間  が与えられたとき, 結合点
が与えられたとき, 結合点  に最も早く到達しうる時刻を最早結合点時刻(earliest node time)
に最も早く到達しうる時刻を最早結合点時刻(earliest node time) 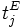 とよび,
とよび,
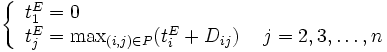
で計算する. ただし,  はプロジェクト全体の作業集合,
はプロジェクト全体の作業集合,  は終点を意味する. この計算は前進計算という. 上式により求めた
は終点を意味する. この計算は前進計算という. 上式により求めた 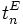 はプロジェクト全体の工期(総所要日数ともいう)を与える. つぎに, この工期から逆算して, 結合点
はプロジェクト全体の工期(総所要日数ともいう)を与える. つぎに, この工期から逆算して, 結合点  に遅くとも到達していなければならない限界の時刻である最遅結合点時刻(latest node time)
に遅くとも到達していなければならない限界の時刻である最遅結合点時刻(latest node time) 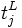 を次式から求める.
を次式から求める.
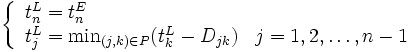
この計算を後進計算という. これらの結合点時刻から, 各作業の開始時刻と終了時刻の限界が次式より求められる.
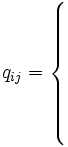 |
最早開始時刻 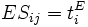 |
最遅開始時刻 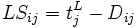 |
|
最早終了時刻 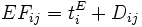 |
|
最遅終了時刻 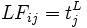 |
最早時刻と最遅時刻とに差異がある場合には, その作業に日程上の余裕があることを意味し, この余裕をフロート(float)とよぶ. 作業 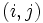 の全余裕時間(total float)
の全余裕時間(total float) 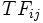 と自由余裕(freefloat)
と自由余裕(freefloat) 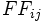 は, 次式から求められる.
は, 次式から求められる.
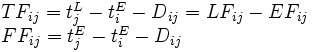
アローダイヤグラムの矢線を順方向にたどって, 始点から終点に至る作業の列をパス(path)とよぶ. とくに 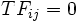 の作業の列で形成されるパスはクリティカルパス(criticalpath)とよばれ, その長さはすべてのパスのうち最長となっている.
の作業の列で形成されるパスはクリティカルパス(criticalpath)とよばれ, その長さはすべてのパスのうち最長となっている.
PERT手法を基礎として種々な拡張が試みられている [3], [4]. 例えば, (i)作業に確率的選択の要素を入れたGERT(graphical evaluation and review technique)やVERT(ventureevaluation and review technique), (ii)PERTの時間的要素とともに費用に関するデータを考慮して, 日程と費用の両面から計画・管理を行うPERT/COST, (iii) 資源制約を考慮して, その山積み・山崩しをアローダイヤグラムを基礎に実施しようとする資源制約付きプロジェクト・スケジューリング, (iv)単一プロジェクトから複数のプロジェクトの管理へ展開するRAMPS(resource allocationand multi-project scheduling), などがある.
また, PERT計算で必要な各作業の所要時間は3点見積法で見積もられることが多い.
(2)CPM: CPMでは, アローダイヤグラムを構成する各作業 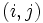 の所要時間が投入費用によって可変であるとし, 両者の間に図3のような線形関係を仮定して日程計算を行う. 各作業を標準時間
の所要時間が投入費用によって可変であるとし, 両者の間に図3のような線形関係を仮定して日程計算を行う. 各作業を標準時間  で行うときの費用を
で行うときの費用を 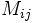 , 特急時間
, 特急時間 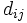 で処理するときの費用を
で処理するときの費用を 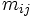 とするとき, 所要時間
とするとき, 所要時間 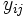 (
( 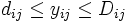 )に対する費用
)に対する費用 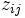 は
は
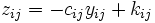
で与えられる. ただし,
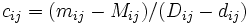
は, 作業を単位時間短縮するのに要する増加費用で, 費用増加率とよばれる. 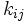 は定数項である.
は定数項である.
CPMは, 以下のように定式化される. アローダイヤグラムの結合点  (
( 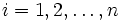 )の結合点時刻を
)の結合点時刻を 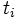 , 達成したいプロジェクト全体の工期を
, 達成したいプロジェクト全体の工期を 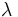 (
( 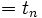 )とすると,
)とすると,
制約条件:
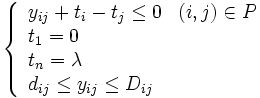
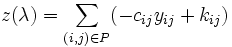
を最小化するような日程計画{  }を求める問題となる. ここで,
}を求める問題となる. ここで,  はプロジェクトの作業集合を意味する.
はプロジェクトの作業集合を意味する.
CPMの解法にはいくつかの方法がある. 1つの方法は, CPM問題を工期 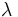 をパラメタとするパラメトリック線形計画法(parametric LP)と見なして解く解法で, プライマル・デュアル法(primal-dual algorithm)に基づく解法が提案されている. より広く使われている解法にラベリング法(labeling algorithm)がある. この方法は, 各作業の費用増加率
をパラメタとするパラメトリック線形計画法(parametric LP)と見なして解く解法で, プライマル・デュアル法(primal-dual algorithm)に基づく解法が提案されている. より広く使われている解法にラベリング法(labeling algorithm)がある. この方法は, 各作業の費用増加率 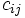 を矢線の容量制約とし, 始点から終点に最大フローを流す問題としてCPM問題を解く方法である. 多くの解法が提案されており, その計算量の比較も行われている [5].
を矢線の容量制約とし, 始点から終点に最大フローを流す問題としてCPM問題を解く方法である. 多くの解法が提案されており, その計算量の比較も行われている [5].
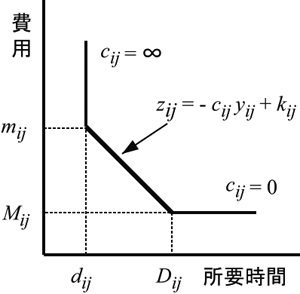 |
図3 費用関数 |
プロジェクト・スケジューリングの最近の研究が [6, 7]にまとめられている.
[1] 関根智明,『PERT・CPM』,日科技連出版社, 1973.
[2] 刀根薫,『PERT入門』,東洋経済新報社, 1977.
[3] S. E. Elmaghraby, Activity Networks, John Wiley & Sons, 1977. 加瀬滋男『アクティビティネットワーク』,日刊工業新聞社, 1979.
[4] S. I. Gass and C. M. Harris, eds., Encyclopedia of Operations Research and Management Science, Kluwer Academic, 1996. 森村英典, 刀根薫, 伊理正夫監訳,『経営科学OR用語大辞典』,朝倉書店, 1999.
[5] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, "Network Flows," in Optimization, G. L. Nemhauser, A. H. G. Rinnooy Kan and M. J. Todd, eds., North-Holland, 1989.
[6] L. V. Tavares, Advanced Models for Project Management, Kluwer Academic, 1999.
[7] J. Weglarz, ed., it Project Scheduling: Recent Models, Algorithms and Applications, Kluwer Academic Publishers, 1999.
| 企画・開発・プロジェクト・品質・ヒューマン: | パレート図 ヒストグラム フロート プロジェクト管理 マトリックスデータ解析法 マトリックス図法 乗務員スケジューリング問題 |
ぷろじぇくとかんりと同じ種類の言葉
- ぷろじぇくとかんりのページへのリンク
