一様乱数
【英】:uniform random numbers
概要
すべての値の出現確率が等しい乱数のこと. 離散型の一様乱数の場合は,とりうる値の集合としてふつう (
(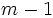 は計算機で表現できる最大の自然数に近い数), あるいは, この中から等間隔に抽出した数の集合を想定する. 離散型の一様乱数を
は計算機で表現できる最大の自然数に近い数), あるいは, この中から等間隔に抽出した数の集合を想定する. 離散型の一様乱数を で割ったものを近似的に区間[0,1)上の連続一様分布にしたがう乱数と見なして, 標準一様乱数という.
で割ったものを近似的に区間[0,1)上の連続一様分布にしたがう乱数と見なして, 標準一様乱数という.
詳説
確率変数の実現値と見なしうる数の列のことを乱数 (または乱数列)(random numbersまたはrandom number sequence)という. 確率変数の従う分布として一様分布を想定する場合には, 対応する乱数のことを一様乱数 (uniform random numbers)という. 例えば, サイコロを振って出る目(数)の系列は, 典型的な一様乱数である. この系列には次の2つの性質がある. 1) 系列が長ければ各数の相対出現頻度がほぼ等しい. 2) 次に出る数を確実に予測することは不可能である.
大量の乱数を使用する実験では, サイコロを振って乱数を作るのは現実的でないので, 簡単なアルゴリズムで生成される乱数もどきの数(擬似乱数)で代用するのがふつうである. そして, これを単に乱数と呼ぶことが多い. この意味での乱数は, 上記の2) の性質は持たないが, 1) の性質は近似的に満たしているものと考えられている. このような乱数の生成法は数多く提案されているが, 現在比較的よく使われているものを以下にあげる.
[線形合同法]
1948年頃にレーマー(Lehmer)によって提案され, その後多数の人々によって研究された方法であり, 線形漸化式
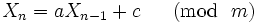
を使って非負整数列 を生成する. ここで,
を生成する. ここで, 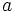 および
および は正整数であり,
は正整数であり, 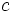 は非負整数である. 特に
は非負整数である. 特に の場合には, 乗算合同法と呼ぶ. パラメタの選び方に関しては多くの研究結果があるが, 現在比較的良いとされているものをいくつか表1に示す.
の場合には, 乗算合同法と呼ぶ. パラメタの選び方に関しては多くの研究結果があるが, 現在比較的良いとされているものをいくつか表1に示す.
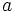 |
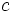 |
 |
 |
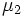 |
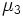 |
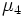 |
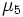 |
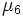 |
周期 |
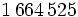 |
 |
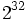 |
任意 | 16.1 | 10.6 | 8.0 | 6.0 | 5.0 | 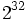 |
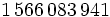 |
0 | 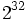 |
奇数 | 14.8 | 9.7 | 7.5 | 5.6 | 4.2 | 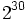 |
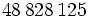 |
0 | 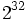 |
奇数 | 14.8 | 8.8 | 7.4 | 5.7 | 4.9 | 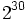 |
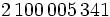 |
0 |  |
正整数 | 15.4 | 10.2 | 7.7 | 6.0 | 5.0 | 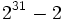 |
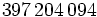 |
0 |  |
正整数 | 14.8 | 9.7 | 7.4 | 6.0 | 5.0 | 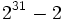 |
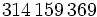 |
0 |  |
正整数 | 15.2 | 9.9 | 7.6 | 5.9 | 5.1 | 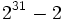 |
線形合同法によって生成される乱数の欠点として, 多次元疎結晶構造と言われているものがある. これは,  次元超立方体内にランダムに点を配置する目的で, 点の座標を
次元超立方体内にランダムに点を配置する目的で, 点の座標を で定めたとすると, これらの点はすべて比較的少数の等間隔に並んだ超平面の上に規則的にのってしまい, ランダムにならないという性質である.
で定めたとすると, これらの点はすべて比較的少数の等間隔に並んだ超平面の上に規則的にのってしまい, ランダムにならないという性質である.  と超平面の枚数の上界との関係を表2に示す. また, 表1の
と超平面の枚数の上界との関係を表2に示す. また, 表1の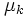 は,
は,  次元の点配置を作ったとき,
次元の点配置を作ったとき, 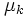 ビットの精度ではほぼ一様な配置になることを意味している.
ビットの精度ではほぼ一様な配置になることを意味している.
 |
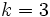 |
4 | 5 | 6 | 7 | 8 | 9 | 10 |
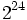 |
465 | 141 | 72 | 47 | 36 | 30 | 26 | 23 |
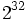 |
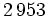 |
566 | 220 | 120 | 80 | 60 | 48 | 41 |
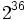 |
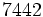 |
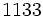 |
383 | 191 | 119 | 85 | 66 | 54 |
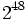 |
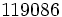 |
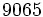 |
 |
766 | 391 | 240 | 167 | 126 |
[M系列法]
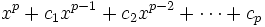
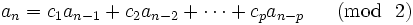
によって生成される系列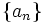 を考える. この系列はM系列(M-sequence)あるいはシフトレジスタ系列, 極大多項式系列などと呼ばれ,
硬貨を投げて表が出れば1, 裏が出れば0として得られる系列と類似の性質を持つことが知られている.
表3に実用的な原始多項式の例を示す.
を考える. この系列はM系列(M-sequence)あるいはシフトレジスタ系列, 極大多項式系列などと呼ばれ,
硬貨を投げて表が出れば1, 裏が出れば0として得られる系列と類似の性質を持つことが知られている.
表3に実用的な原始多項式の例を示す.
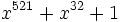 |
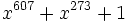 |
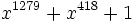 |
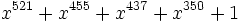 |
 |
これは1ビットの系列なので, 多数ビットの系列 を作るためには, 漸化式
を作るためには, 漸化式
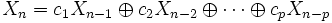
を用いる. ここで, 記号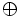 は2進法でのけた上りなしの足し算(ビットごとの排他的論理和)を表す. これによって生成される系列は, トーズワース(Tausworthe)系列あるいはGFSR(Generalized Feedback Shift Register)系列と呼ばれている.
は2進法でのけた上りなしの足し算(ビットごとの排他的論理和)を表す. これによって生成される系列は, トーズワース(Tausworthe)系列あるいはGFSR(Generalized Feedback Shift Register)系列と呼ばれている.
この漸化式を使う場合の初期値の設定法については, [1] を参照するとよい. これを使って例えば32ビットの整数系列 を生成すると, 合同法のような多次元疎結晶構造が生じることはなく, 32ビットの精度で
を生成すると, 合同法のような多次元疎結晶構造が生じることはなく, 32ビットの精度で![[p/32] \,](https://cdn.weblio.jp/e7/img/dict/orjtn/da6e59b59070940e576165dfefd6ee85.png) 次元まで一様に分布する. また, この系列の周期は
次元まで一様に分布する. また, この系列の周期は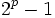 であり, 自己相関関数の値は位相差が
であり, 自己相関関数の値は位相差が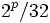 以下ならばほぼ0に等しい.
以下ならばほぼ0に等しい.
M系列を使ったもう少し複雑な乱数生成法として, 最近提案されたメルセンヌ・ツイスター(Mersenne Twister) [3] がある. これは上記のものに比べて, 同じ記憶容量で, はるかに長い周期と高い次元の一様性を達成できるという特徴を有する. 詳細は
http://www.math.keio.ac.jp/
を参照するとよい.
[1] 伏見正則, 『乱数』(UP応用数学選書12), 東京大学出版会, 1989.
[2] D. E. Knuth, The Art of Computer Programming, Vol.2: Seminumerical Algorithms, 2nd ed., Addison-Wesley, 1981. 渋谷政昭訳, 『準数値算法/乱数』, サイエンス社, 1981.
[3] M. Matsumoto and T. Nishimura, "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator," ACM Transactions on Modeling and Computer Simulation, 8 (1998), 3-30.
一様乱数と同じ種類の言葉
- 一様乱数のページへのリンク
