ANP
【英】:ANP (analytic network process)
概要
AHPの階層構造をネットワーク構造に拡張したもの. AHPの評価構造は評価基準が代替案を評価するというように, 評価者と被評価者の区別が固定しているが, ANPでは, 被評価者自身が, 評価者の評価の重要度あるいは評価能力を評価するという問題をも取り扱う. サーティ (T.L. Saaty) はこの評価構造の関連を超行列という一種の確率行列で表現し, その累乗の極限によって分析する方法を示した.
詳説
AHPの特徴は, 一対比較の情報に基づいて固有ベクトル法を用いて各対象の評価値を推定するという面と, いくつかの評価基準の下での評価値を総合化するという階層構造にあった. T. L. Saatyの提案したANPというのは, 簡単に言うと, その階層構造をネットワーク構造に拡張したものである. Saatyはこのネットワーク構造の解析の基本として, 超行列とよばれる行列を導入し, その行列としての性質, 既約性や原始性を利用して解析法を確立した.
[超行列]
はじめに簡単な例を通して, ANPの特徴をつかもう. たとえば食品産業の3社 を代替案とみて, これらを2つの評価基準
を代替案とみて, これらを2つの評価基準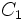 (広告),
(広告), 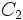 (サービス)で評価するという問題を考えよう.
(サービス)で評価するという問題を考えよう.  の
の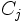 による評価値が
による評価値が であるとしてこれらを列挙すると表1のようになる.
であるとしてこれらを列挙すると表1のようになる. 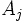 の企業戦略として広告とサービスにそれぞれ
の企業戦略として広告とサービスにそれぞれ ,
,  の重要度を考えているとすると
の重要度を考えているとすると ,
, 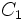 ,
, 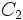 の重要度の評価は, AHPのように一組だけでなく,
の重要度の評価は, AHPのように一組だけでなく, 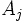 によって変化して表2のようになる.
によって変化して表2のようになる.
表1:  の の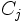 による評価 による評価 |
 |
表2:  の の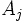 による評価 による評価 |
 |
これは が
が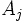 を評価するだけでなく,
を評価するだけでなく, 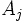 自身が
自身が の重要度を評価することを示している. つまりANPでは, 評価者と被評価者の区別が固定したものでなく, 互いに他を評価するという一種の相互評価の構造がある.
の重要度を評価することを示している. つまりANPでは, 評価者と被評価者の区別が固定したものでなく, 互いに他を評価するという一種の相互評価の構造がある.
対象 の
の による評価値(評価がない場合は0)を
による評価値(評価がない場合は0)を 行
行 列として得られる行列が超行列(super matrix)と呼ばれるものである. 上の例の超行列は
列として得られる行列が超行列(super matrix)と呼ばれるものである. 上の例の超行列は
 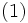 |
ANPの解析の目的はこの超行列が与えられたとき, 各対象(上例では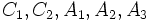 )の総合評価値を求めることである. またANPでは与えられる評価値はすべて正であり, 一つの対象が与える評価値の総和は1であるという規約がある. つまり超行列の各列の要素の和は1である. このことは超行列が(列)確率行列であることを示している.
)の総合評価値を求めることである. またANPでは与えられる評価値はすべて正であり, 一つの対象が与える評価値の総和は1であるという規約がある. つまり超行列の各列の要素の和は1である. このことは超行列が(列)確率行列であることを示している.
[ネットワーク構造]
対象 が
が を評価するとき(つまり超行列の
を評価するとき(つまり超行列の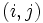 要素が非ゼロのとき)そしてそのときに限り, 点
要素が非ゼロのとき)そしてそのときに限り, 点 から点
から点 への矢線をもつ有向グラフが得られるが, これをこのANPのネットワーク構造と呼ぶ. 上例に対するネットワークは図1のようになる. このグラフ構造の特徴が超行列
への矢線をもつ有向グラフが得られるが, これをこのANPのネットワーク構造と呼ぶ. 上例に対するネットワークは図1のようになる. このグラフ構造の特徴が超行列 の行列としての性質に密接に関連していて, それがANPの解析を特徴づける.
の行列としての性質に密接に関連していて, それがANPの解析を特徴づける.
すでにAHPの中に外部従属法という解析法があるが, これはANPの特殊なもので, そのネットワーク構造が図1のように2部グラフの形をしたものである. ANPの新しさは, このネットワーク構造がどんなものであっても, 超行列を基本として一貫した解析法で総合評価値を求めることができることにある.
 |
| 図1: ネットワーク構造 |
[ANPの解法]
SaatyのANPの解法は, 超行列の累乗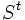 の
の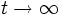 での極限を利用するものであるが,
での極限を利用するものであるが,  の行列としての性質によって, その収束状態が異なってくる.
の行列としての性質によって, その収束状態が異なってくる.
一般に行列の性質はそれに対応する有向グラフの特性と密接に関連する. 行列論でいう行列の既約性 (irreducibility)は, 対応する有向グラフが強連結であることと同値である. (有向グラフの任意の2点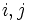 に対して
に対して から
から への有向パスがあれば, このグラフを強連結という).
への有向パスがあれば, このグラフを強連結という).
また非負の既約行列 が原始(primitive)であるとは, 適当な自然数
が原始(primitive)であるとは, 適当な自然数 に対して
に対して の要素がすべて正となることであるが, これはこの行列に対応する有向グラフの周期が1であることと同値である [1]. 周期とはすべての有向サイクル(ある点からその点にはじめて戻る有向パス)の長さの最大公約数
の要素がすべて正となることであるが, これはこの行列に対応する有向グラフの周期が1であることと同値である [1]. 周期とはすべての有向サイクル(ある点からその点にはじめて戻る有向パス)の長さの最大公約数 である. 図1での有向サイクルの長さは,
である. 図1での有向サイクルの長さは,  であるので周期は
であるので周期は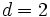 である.
である.
超行列 に対応する有向グラフの周期
に対応する有向グラフの周期 がANPの解法に重要な役割を果たす. SaatyによるANP解法の基本はつぎの定理に要約される [1]:
がANPの解法に重要な役割を果たす. SaatyによるANP解法の基本はつぎの定理に要約される [1]:
定理 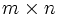 超行列
超行列 が既約であってかつ原始(
が既約であってかつ原始( に対応する有向グラフの周期が1)であれば,
に対応する有向グラフの周期が1)であれば, 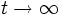 で
で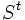 は収束しその極限値
は収束しその極限値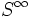 はすべての列が同一ベクトル
はすべての列が同一ベクトル  となる. つまり
となる. つまり
![lim_{t\to\infty}S^t=S^{\infty}=[ \mathbf{x} \mathbf{x} \cdots \mathbf{x} \mathbf{x}]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/5edd57a0a60559c442741c315b93a2e5.png)
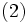
定理 超行列 が既約であって, 対応する有向グラフの周期を
が既約であって, 対応する有向グラフの周期を とするとき
とするとき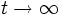 で
で が収束し, その極限値で行と列を適当に並べかえたものを
が収束し, その極限値で行と列を適当に並べかえたものを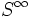 とすると, これは
とすると, これは 位のブロック対角行列となり, 各ブロック内ではすべての列が同一ベクトルとなる.
位のブロック対角行列となり, 各ブロック内ではすべての列が同一ベクトルとなる.
たとえば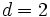 なら
なら
![\begin{array}{ccc}
S^{\infty}=
\left[
\begin{array}{cc}
S_1 & O \\
O &S_2 \\
\end{array}
\right]
& , &
\begin{array}{c}
S_1=[ \mathbf{x}_1 \mathbf{x}_1\cdots \mathbf{x}_1] \\
S_2=[ \mathbf{x}_2 \mathbf{x}_2\cdots \mathbf{x}_2] \\
\end{array}
\end{array}\,](https://cdn.weblio.jp/e7/img/dict/orjtn/4d0438bc4af0ba8a8df3f20ce8e38459.png)
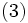
最近, 高橋, 関谷 [2], [3] は,  が既約ならば,
が既約ならば,  の主固有ベクトルが(2)等の収束ベクトル
の主固有ベクトルが(2)等の収束ベクトル  に一致することを示している.
に一致することを示している.  が確率行列であるから, その主固有値は1であり,
が確率行列であるから, その主固有値は1であり,  の主固有ベクトル
の主固有ベクトル  は
は

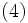
の解であるが, これが(2)の  と(定数倍を除いて)一致することが示されたのである.
と(定数倍を除いて)一致することが示されたのである.  が原始でない場合でも(4)の解はたとえば(3)の
が原始でない場合でも(4)の解はたとえば(3)の  をそのまま縦に並べたものと一致する.
をそのまま縦に並べたものと一致する.
これによるとANPの解法は極めて簡単で超行列の主固有ベクトルを求めればよいということになる. また「非負の既約行列の主固有ベクトルは(定数倍を除いて)一意であり, その成分はすべて正である」 [4] というフロベニウスの定理から, (4)の解の一意性とその値がすべて正となることが保証される.
以上の解法はいずれも超行列が既約であること, つまりネットワーク構造が強連結であることを前提としている. しかし [2] には必ずしも強連結でない場合についてもその解法が提案されている.
[1] T. L. Saaty, The Analytic Network Process, RWS Publication, 1996.
[2] K. Sekitani and I. Takahashi, " Unified Model and Analysis for AHP and ANP," Journal of the Operations Research Society of Japan, 44 (2001), 67-89.
[3] 高橋磐郎, 『AHPからANPへの諸問題』, オペレーションズ・リサーチ, 43 (1998), 289-293.
| AHP(階層的意思決定法): | AHP外部従属法 AHP相対評価法 AHP絶対評価法 ANP CIミニマム法 Perron-Frobenius定理 グループAHP |
- えいえぬぴーのページへのリンク
![\mathbf{x}=[x_1x_2\cdots x_n]^{\top}\,](https://cdn.weblio.jp/e7/img/dict/orjtn/9fd5c0ea28d67282876d6b7e2e54d3ac.png) の
の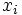 を
を の各
の各