最小木問題
【英】：minimum spanning tree problem
概要
各枝に重みの与えられた(無向)グラフにおいて, そのグラフ上に存在する全張木(全域木)の中で枝の重みの総和が最小になるものを見出す組合せ最適化問題. それ自身も多くの応用例をもつが, より複雑な問題の子問題として利用されることも多い. クラスカル法やプリム法といった貪欲アルゴリズムにより多項式時間で解くことが可能である.
詳説
無向グラフ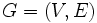
の各枝
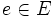に実数の重み
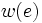が与えられているとする. グラフ
上において全点
を点集合とし木になっている部分グラフを全張木あるいは全域木(spanning tree)と呼ぶ. グラフ上の全張木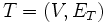
の重みは,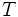 
上の枝の重みの総和
で定める. グラフ上において重み最小の全張木を最小木 (minimum spaninng tree) といい, 最小木を求める問題を最小木問題 (minimum spaninng tree problem) という.
最小木問題は, クラスター分析やネットワーク・デザインなどの分野で利用されているが, より複雑な問題の子問題として活用されることの多い基本的な問題である([2]).
グラフ上の問題として基本的である最小木問題がいつ頃から考えられたのかは明らかではない. 分かっている範囲では, 1926年に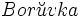
が,またそれとは独立に, 1930年にJarníkがそれぞれ最小木問題を定式化しそのアルゴリズムを発表している（最小木問題に関する歴史は [4] が詳しい). その後,最小木問題に対する基本的なアルゴリズムとしてクラスカル法(Kruskal's algorithm) とプリム法(Prim's algorithm) などが提案された. 現在までに提案されている主な効率的なアルゴリズムはこれらの二つのアルゴリズムのどちらかを基にデータ構造を工夫することによって構築されている([1, 8]).
クラスカル法は, 1956年に J. B. Kruskal [6] により, またそれとは独立に1957年にH. LobermanとA. Weinbergerにより提案された多項式時間アルゴリズムである. アルゴリズムの概要は以下のとおりである. クラスカル法では，まず, 枝のない点集合のみからなる森
)を考え，次に, 閉路が発生しない限り枝の重みが小さい順に一本ずつ森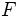
に枝を加えるという操作を繰り返す. 森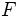が全張木になった時点で繰り返しは終了し, 得られた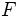が一つの最小木である.
一方, プリム法は, 1957年, R. C. Prim [7] によって提案された多項式時間アルゴリズムである(Jarník法と同様). プリム法では, まず, 任意の１点
のみからなる木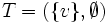
を考え, 次に, グラフにおいて現在の木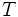の点集合と木以外の点集合を接続する枝集合の中から枝の重みが最も小さい枝とその端点を新たに木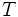に加えるという操作を繰り返す. 木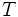がグラフの全張木になった時点で繰り返しは終了し, 得られた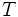が一つの最小木である.
どちらのアルゴリズムも候補の枝集合から最小の重みの枝を選びながら最小木を構成していくという点から貪欲アルゴリズム (greedy algorithm) という種類に分類されるアルゴリズムである. クラスカル法とプリム法の違いは候補の枝集合の構成法にある. プリム法は与えられたグラフの点と枝の接続関係に強く依存したアルゴリズムであって, そのアルゴリズムの構造は最短路問題のダイクストラ法と全く同じである．一方, クラスカル法は，グラフのマトロイド構造にのみ依存したアルゴリズムであって, マトロイドの最小基問題に対する貪欲アルゴリズムへと一般化されている．逆に, このような貪欲アルゴリズムが最適解を見出す問題はマトロイド構造を持つことも知られている．
クラスカル法やプリム法のような貪欲アルゴリズムの考え方を用いたアルゴリズムは組合せ最適化の分野において数多く見受けられる. この貪欲アルゴリズムの考え方で解ける抽象的な組合せ最適化問題のクラスはマトロイド最適化問題と呼ばれ, そのクラスが持つ性質はマトロイド理論として組合せ最適化における多くの有用な知見を提供している[8].
最小木問題は無向グラフ上において定義された問題であるが, 枝の向きに依存した有向グラフ上の問題も考えられる. 有向グラフ上での全張木は，根と呼ばれる１点から他の点への有向道がその全張木上に存在するとき有向木 (directed tree) あるいは根つき木 (rooted tree) と呼ばれる. 枝の重みの総和が最小となる有向木を求める問題は無向グラフ上の最小木を求めるほど簡単ではないが, 多項式時間アルゴリズムが存在する[8].
最小木問題は重み最小の全張木を求める問題であるが, 「全張木」を「ある与えられた点集合
を連結化する木」と変更してみる. この変更された問題をシュタイナー最小木問題 (または, シュタイナー木問題) と呼び, その最適解をシュタイナー最小木と呼ぶ. 与えられた無向グラフの各枝の重みがすべて正である時, シュタイナー木の葉は点集合
に属する点となり, 内点は点集合に属さない点（シュタイナー点と呼ばれる）をいくつか含む.
シュタイナー最小木問題は,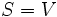 
の時に最小木問題と同一になり, また, 
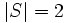かつ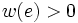
の時は最短路問題と同一になるので, これらの基本的な問題の一般化として捉えることができる. 最小木問題や最短路問題には多項式時間アルゴリズムが存在するが, シュタイナー木問題はNP困難であることが示され, 多項式時間アルゴリズムの存在は絶望視されている. 問題を解く困難性は平面グラフに限定した場合でも, また各枝の重みが等しい場合でも変わらない [3].
問題を解く困難性はあるが, シュタイナー最小木問題は通信ネットワーク, 電力供給網において顧客を結ぶネットワーク上の問題や施設配置問題などの子問題として多くの応用例を有する. その必要性からシュタイナー最小木問題に対して多くの近似解法が提案されてきている [5].
参考文献
[1] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, Network Flows: Theory, Algorithms, and Applications, Prentice Hall, New Jersey, 1993.
[2] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, "Applications of Network Optimization," in Network Models, M. O. Ball, T. L. Magnanti, C. L. Monma and G. L. Nemhauser, eds., North-Holland, 1995.
[3] M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-completeness, Freeman, San Francisco,1979.
[4] R. L. Graham and P. Hell, "On the history of minimum spanning tree problem," Annals of the History of Computing, 7 (1985), 43-57.
[5] F. W. Hwang, D. S. Richards and P. Winter, The Steiner Tree problem, Annals of Discrete Mathematics 53, North-Holland, Amsterdam,1992.
[6] J. B. Kruskal, "On the shortest spanning tree of a graph and the traveling salesman problem," Proceedings of the American Mathematical Society, 7 (1956), 48-50.
[7] R. C. Prim, "Shortest connection networks and some generalizations," Bell System Technical Journal, 36 (1957), 1389-1401.
| グラフ･ネットワーク： | 最大フローアルゴリズム 最大フロー最小カット定理 最大マッチング最小被覆定理 最小木問題 最小費用フロー問題 最短路問題 最近近傍法 |
| 組合せ最適化： | 整数計画 施設配置問題 最大クリーク問題 最小木問題 最短路問題 最適性の原理 木 |
「minimum spanning tree problem」の例文・使い方・用例・文例
- minimum spanning tree problemのページへのリンク
