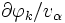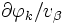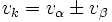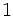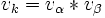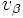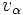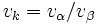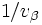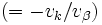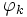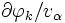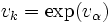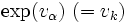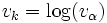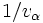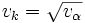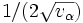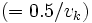高速微分法
【英】:fast differentiation
非線形関数の勾配, ヤコビ行列, ヘッセ行列等の値を数値的に計算する方法のひとつ. 高速自動微分法(fast automatic differentiation), 計算微分法(computational differentiation), 単純に自動微分(automatic differentiation; 以下 AD)ともいう. 主なアルゴリズムは2種あり, ボトムアップ(前進)自動微分(bottom-up AD, forward AD; 以下 BUAD) と, トップダウン(逆行)自動微分(top-down AD, reverse AD, backward AD; 以下 TDAD) という [1, 2]. 高速微分法は狭義には, TDADを指す. AD は「関数の値を計算するプログラム」から「偏導関数の値を計算するプログラム」を生成する手順を与え, 生成物を(コンパイルし)実行すれば, 差分商近似のような打ち切り誤差無しで, 正確な偏導関数の値を計算できる. 大規模システムの数学モデル等の大規模プログラム(数千行以上)により表現される関数の偏導関数を計算できるのが特長.  変数関数の勾配の
変数関数の勾配の 個の値を関数計算の手間の定数倍で計算できる点が「高速」微分の由来である.
個の値を関数計算の手間の定数倍で計算できる点が「高速」微分の由来である.
以下,BUAD と TDAD による計算法を説明する.例として,2変数関数 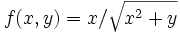 について,
について, 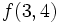 の値を計算する代入文の列(プログラム),
の値を計算する代入文の列(プログラム), 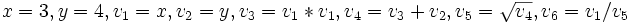 を考えよう. ただし, 各代入文の右辺には, 演算(基本演算とよぶ)が高々1回だけ現れるとする.
を考えよう. ただし, 各代入文の右辺には, 演算(基本演算とよぶ)が高々1回だけ現れるとする. 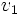 ,
, 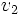 が
が  ,
, 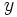 に対応し,
に対応し,  に
に 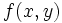 の値が計算される. 一般には,
の値が計算される. 一般には,  変数関数
変数関数  について,
について,  回目の代入文には,
回目の代入文には, 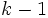 回目までに計算される変数が現れうるから, 延べ
回目までに計算される変数が現れうるから, 延べ 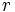 回の演算を行なう代入文の列は
回の演算を行なう代入文の列は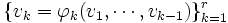 と表される. これを計算過程といい,
と表される. これを計算過程といい, 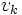 を中間変数という.
を中間変数という. 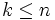 のとき
のとき 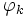 は
は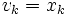 という入力定数の代入演算に相当する.
という入力定数の代入演算に相当する.
BUADは, 補助変数 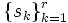 を導入し, 任意に
を導入し, 任意に 
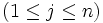 を固定して, 合成関数の
を固定して, 合成関数の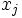 に関する偏微分則
に関する偏微分則 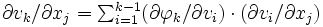 に基づき,
に基づき, 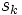 を計算する式を導出する. 基本演算
を計算する式を導出する. 基本演算 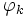 を四則演算や初等関数などの2項・単項の演算に限れば, 表1により,
を四則演算や初等関数などの2項・単項の演算に限れば, 表1により, 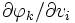 (これを要素的偏導関数という)を導出できる.
(これを要素的偏導関数という)を導出できる. 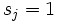 ,
, 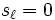
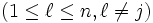 と初期設定すれば,
と初期設定すれば, 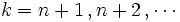 について
について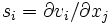
 を計算済みとみなすことができ,
を計算済みとみなすことができ, 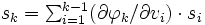 の値を計算できる. 最終的に
の値を計算できる. 最終的に 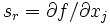 となる.
となる.
先の例では, 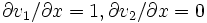 に注意して,
に注意して, 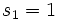 ,
, 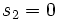 ,
, 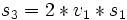 ,
, 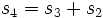 ,
, 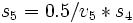 ,
, 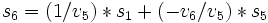 という代入文の列を生成する. これを実行すると
という代入文の列を生成する. これを実行すると 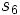 には
には 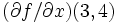 の値が計算される(
の値が計算される(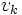 の計算の直後に
の計算の直後に 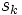 を計算してもよい). 高々2項までの基本演算だけ使用するという条件の下では, BUADの手間は
を計算してもよい). 高々2項までの基本演算だけ使用するという条件の下では, BUADの手間は 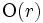 である.
である. 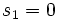 ,
, 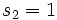 と一部変更し, もう一度計算すれば,
と一部変更し, もう一度計算すれば, 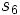 には,
には, 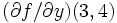 の値が計算される.
の値が計算される.  変数関数の勾配を計算するには, 同様の計算を
変数関数の勾配を計算するには, 同様の計算を  回繰り返す必要がある.
回繰り返す必要がある.
TDADはこれとは異なり, 先の計算過程を  と書き直し, これらを
と書き直し, これらを  に関する制約式とみなす. この制約の下で,
に関する制約式とみなす. この制約の下で, 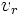 (
( の値) の停留点を考える. ラグランジュ関数
の値) の停留点を考える. ラグランジュ関数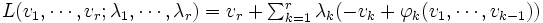 の停留点(
の停留点(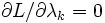 かつ
かつ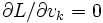 が成立する点)では, ラグランジュ乗数
が成立する点)では, ラグランジュ乗数 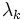 は,
は,  番目の制約式の摂動に対する関数値
番目の制約式の摂動に対する関数値 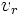 の感度を与えるが,
の感度を与えるが, 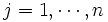 については
については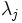 は
は 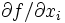 に等しい. 入力
に等しい. 入力  を定めると
を定めると は一意に定まるが,
は一意に定まるが, 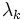 は連立一次方程式
は連立一次方程式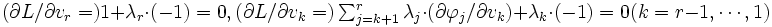 を満たす. これを解くには,
を満たす. これを解くには, 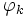 が実質的に単項・2項演算であることを考慮すると,
が実質的に単項・2項演算であることを考慮すると, 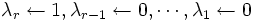 と初期化しておき,
と初期化しておき, 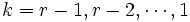 の順に
の順に 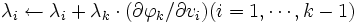 を計算する. 各
を計算する. 各  について高々2個の
について高々2個の  についてだけ計算すればよい.
についてだけ計算すればよい.
先の例では,  を計算し,
を計算し,  と初期化した後,
と初期化した後, 
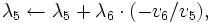
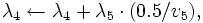
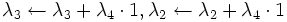 ,
, 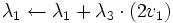 となる. 最終的に
となる. 最終的に 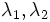 に
に 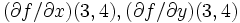 の値が計算される. 同じ条件の下で, TDADの手間は
の値が計算される. 同じ条件の下で, TDADの手間は 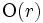 である. 1回の計算で勾配の値は全て計算できることに注意.
である. 1回の計算で勾配の値は全て計算できることに注意.
 変数
変数  値関数
値関数 ![[f_1(x_1,\cdots,x_n),\cdots,f_m(x_1,\cdots,x_n)]^{\top}](https://cdn.weblio.jp/e7/img/dict/orjtn/7789da21ab0e3be3963c5b69527a45be.png) について, 全成分の値を計算するのに延べ
について, 全成分の値を計算するのに延べ 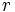 回の基本演算を実行したとする. ヤコビ行列
回の基本演算を実行したとする. ヤコビ行列 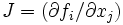 の列の線形結合はBUADで, 行についてはTDADで
の列の線形結合はBUADで, 行についてはTDADで 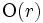 の手間で計算できる. 全成分については BUADでは
の手間で計算できる. 全成分については BUADでは 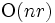 , TDAD では
, TDAD では 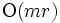 である.
である.
実際には, 基本演算は表1に限らず, 代入文(やその列)を一つの基本演算とみなしてよい. また, プログラム中に条件分岐があっても, 与えられた入力値に関する関数の合成は上記の形で書けるから, ADを適用できる. ただし, 分岐の境目では, ADの結果は, 真の偏導関数値と異なることがある. たとえば, 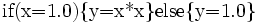 の様なプログラムを自動微分すると,
の様なプログラムを自動微分すると,  の値が1.0 のときには不具合が起こりうるので注意が必要である.
の値が1.0 のときには不具合が起こりうるので注意が必要である.
[1] M.Bucker, G.Corliss, P.Hovland, U.Naumann, and B.Norris (eds.), Automatic Differentiation: Applications, Theory, and Implementations, Lecture Notes in Computational Science and Engineering, Springer, Vol.50, 2006.
「fast differentiation」の例文・使い方・用例・文例
- fast differentiationのページへのリンク