マッチング問題
【英】:matching problem
概要
無向グラフが与えられたときに, ある目的にしたがってマッチングを選ぶ問題をマッチング問題と呼ぶ. 例えば, 最大要素マッチング問題, 最大重みマッチング問題(割当問題), 安定なマッチングを求める安定結婚問題などが挙げられる. 2部グラフでのマッチング問題はネットワークフロー問題の特殊ケースとして解くことができるのに対し, 一般のグラフの場合は問題の構造がより複雑になり多少工夫を要するが, いずれの問題も多項式時間で解くことができる.
詳説
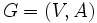 を無向グラフとする.
を無向グラフとする.  のマッチング (matching) とは, 端点を共有しない枝の集合
のマッチング (matching) とは, 端点を共有しない枝の集合 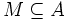 のことである.
のことである.  本の枝からなるマッチングを
本の枝からなるマッチングを  -マッチングと呼び, 特に
-マッチングと呼び, 特に 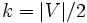 のときは完全マッチングと呼ぶ. 与えられた目的に従ってマッチングを選ぶ問題のことを, マッチング問題という. 以下, 幾つかのマッチング問題について簡単に説明する.
のときは完全マッチングと呼ぶ. 与えられた目的に従ってマッチングを選ぶ問題のことを, マッチング問題という. 以下, 幾つかのマッチング問題について簡単に説明する.
(a) 最大マッチング問題 枝数が最大のマッチングを求める問題を, 最大マッチング問題という. マッチング 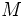 に対し, 長さが奇数の道
に対し, 長さが奇数の道 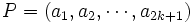 が, 条件
が, 条件 
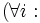 奇数),
奇数), 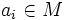
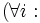 偶数
偶数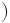 を満たし、道
を満たし、道 の始点と終点が
の始点と終点が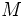 の端点でないとき,
の端点でないとき,  は
は 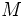 に関する増加道と呼ばれる. 増加道に関して, 以下の性質が成り立つ:
に関する増加道と呼ばれる. 増加道に関して, 以下の性質が成り立つ:
従って, 枝数 0 のマッチングからはじめ, 各反復では, 増加道を求めてマッチングの枝数を増やしていくことで, 最大マッチングが求められる.  が2部グラフの場合には, 増加道の存在判定及び検出が容易に実行できるのに対し, 一般のグラフの場合には多少工夫を要する. いずれの場合も多項式時間で最大マッチングを求めることができる.
が2部グラフの場合には, 増加道の存在判定及び検出が容易に実行できるのに対し, 一般のグラフの場合には多少工夫を要する. いずれの場合も多項式時間で最大マッチングを求めることができる.
点集合 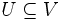 に対して, 任意の枝
に対して, 任意の枝 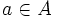 の端点のうち少なくとも一方が
の端点のうち少なくとも一方が 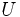 に含まれるとき,
に含まれるとき, 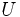 は
は  の被覆 と呼ばれる. 任意のマッチング
の被覆 と呼ばれる. 任意のマッチング 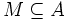 と任意の被覆
と任意の被覆 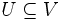 に対して, 不等式
に対して, 不等式 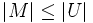 が成り立つ. 特に,
が成り立つ. 特に,  が2部グラフならば, 最大マッチングの枝数と最小被覆の点数は等しい:
が2部グラフならば, 最大マッチングの枝数と最小被覆の点数は等しい:
これを, 2部グラフに関する最大マッチング最小被覆定理という.
一般のグラフの場合, 式(1)は成り立つとは限らないが,成り立つようにその右辺を修正することができる.奇数個の点からなる点集合の族を  とする. 任意の枝
とする. 任意の枝 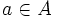 に対して, 以下の条件 (i) または (ii) が成り立つとき,
に対して, 以下の条件 (i) または (ii) が成り立つとき, 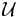 を
を  の奇被覆と呼ぶ:
の奇被覆と呼ぶ:
各 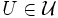 に対し,
に対し, 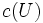 を,
を, 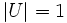 ならば
ならば 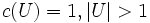 ならば
ならば 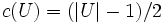 , と定める. このとき, 次の最大・最小定理が成り立つ:
, と定める. このとき, 次の最大・最小定理が成り立つ:
2部グラフ  において,
において, 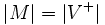 であるマッチング
であるマッチング 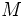 を, 左側端点集合
を, 左側端点集合  に関する完全マッチングという. 左側端点集合
に関する完全マッチングという. 左側端点集合  に関する完全マッチングが存在するための必要十分条件は次のように書ける:
に関する完全マッチングが存在するための必要十分条件は次のように書ける:
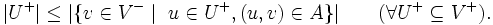
これを, ホールの定理 (Hall's theorem) と呼ぶ.
最小被覆族の構造に基づいた2部グラフの分解としてダルメジ・メンデルゾーン分解 (Dulmage-Mendelsohn decomposition) が知られている. 略してDM分解と呼ばれる. この分解は, 与えられた2部グラフを, 半順序構造を有する部分グラフの族へと一意的に分解する. DM 分解は, 連立一次方程式を解く際にも有用である. 係数行列に関連する2部グラフのDM分解を用いて係数行列のブロック三角化が出来, これにより計算時間を削減することができる.
(b) 最大重みマッチング問題 無向グラフ 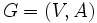 及び各枝
及び各枝 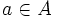 の重み
の重み 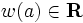 が与えられたとき, 枝重みの和
が与えられたとき, 枝重みの和 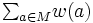 を最大にするマッチング
を最大にするマッチング 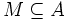 を求める問題を最大重みマッチング問題と呼ぶ. 最大重み
を求める問題を最大重みマッチング問題と呼ぶ. 最大重み -マッチング問題, 最大重み完全マッチング問題も同様に定義される. 2部グラフにおける最大重み完全マッチング問題は割当問題 (assignment problem) とも呼ばれる.
-マッチング問題, 最大重み完全マッチング問題も同様に定義される. 2部グラフにおける最大重み完全マッチング問題は割当問題 (assignment problem) とも呼ばれる.
最大重みマッチングを求めるときも, 最大マッチングと同様に 増加道を用いて繰り返しマッチングの枝数を増やしていき, 最終的に所望のマッチングを求めることができる. その際, 各反復でのマッチングがある種の最適性を満たすように, 増加道をうまく選ぶ必要がある.
一般のグラフの場合には, まず最大重みマッチング問題を線形計画問題として定式化し, そこから現れる相補性条件を考え,その条件が満たされるように増加道を選ぶ. 特に,  が2部グラフの場合は, マッチングの重みの増加量が最大となるように, 各反復において増加道を選べば良い. いずれの場合も, 多項式時間で最大重みマッチングを求めることが出来る. 以上のような主双対算法の他に多くの解法が提案されている.
が2部グラフの場合は, マッチングの重みの増加量が最大となるように, 各反復において増加道を選べば良い. いずれの場合も, 多項式時間で最大重みマッチングを求めることが出来る. 以上のような主双対算法の他に多くの解法が提案されている.
(c) 安定結婚問題 2部グラフでのマッチング問題の一種として, 安定結婚問題が挙げられる. 同じ人数の男性と女性が存在して, 各々が異性に対して結婚相手としての選好順序をもつと仮定する. ここで, 男女を全て結婚させること, すなわち男女間の完全マッチングについて考える. 男女間の完全マッチングが与えられたとき, それが安定であるとは, 結婚していない男性と女性の任意の対 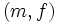 に対して,
に対して,  が
が  より現在の結婚相手を好むか, または
より現在の結婚相手を好むか, または  が
が  より現在の結婚相手を好むことである. 男女間の安定な完全マッチングを求める問題を安定結婚問題と呼ぶ.
より現在の結婚相手を好むことである. 男女間の安定な完全マッチングを求める問題を安定結婚問題と呼ぶ.
安定な完全マッチングは常に存在し, ゲイル・シャプレー(Gale-Shapley) の解法により多項式時間で求められる. この解法では, 各々の男性は1番目に好きな女性から, 2番目に好きな女性, ...と順に, 拒否されたら順位を1つ下げて, 求婚する. 一方, 各々の女性は求婚してきた男性のうち, 最も好きな人との結婚を仮受託し, それ以外の求婚してきた男性を拒否する. この手順を繰り返し, すべての女性が仮受託したら終了であり, 安定な完全マッチングが求められる.
[1] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, Network Flows: Theory, Algorithms, and Applications, Prentice Hall, 1993.
[2] W. J. Cook, W. H. Cunningham, W. R. Pulleyblank and A. Schrijver, Combinatorial Optimization, John Wiley & Sons, 1998.
[3] 藤重悟,『離散数学』, 岩波講座応用数学基礎12, 岩波書店, 1993.
[4] 藤重悟,『グラフ・ネットワーク・組合せ論』, 工系数学講座18, 共立出版, 2002.
[5] D. Gusfield and R. W. Irving, The Stable Marriage Problem: Structure and Algorithms, MIT Press, 1989.
[6] 伊理正夫, 藤重悟, 大山達雄,『グラフ・ネットワーク・マトロイド』, 産業図書, 1986.
[7] B. Korte and J. Vygen, Combinatorial Optimization, 4th ed., Springer, 2007. 浅野孝夫,平田富夫,小野孝男,浅野泰仁訳,『組合せ最適化:理論とアルゴリズム (第2版) 』、シュプリンガー・フェアラーク東京,2005.
[8] E. L. Lawler, Combinatorial Optimization, Networks and Matroids, Holt, Rinehart and Winston, 1976.
[9] L. Lovász and M. D. Plummer, Matching Theory, North-Holland, 1986.
[10] C. H. Papadimitriou and K. Steiglitz, Combinatorial Optimization, Algorithms and Complexity, Prentice-Hall, 1982.
[11] W. R. Pullyblank, "Matchings and Extensions," in Handbook of Combinatorics, Vol. I, R. L. Graham, M. Grötschel and L. Lovász, eds., North-Holland, 1995.
[12] A.Schrijver, Combinatorial Optimization, Polyhedra and Efficiency, Springer, 2003.
| グラフ・ネットワーク: | ホールの定理 ポリマトロイド マッチング マッチング問題 マトロイド ユークリッド巡回セールスマン問題 付値マトロイド |
| 組合せ最適化: | ヒープ ファセット制約 フィボナッチヒープ マッチング問題 メタヒューリスティクス ラグランジュ緩和法 ロバース数 |
- マッチング問題]]のページへのリンク
 は
は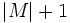 の
の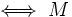
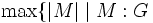 の
の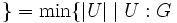 の
の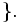
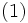
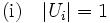 なる
なる 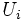 が
が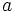 の
の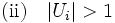 なる
なる 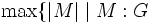 の
の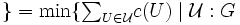 の奇
の奇