アレンジメント【arrangement】
アレンジメント
【英】:arrangement
概要
超平面のアレンジメントとは, 有限個の超平面による空間の分割である. 双対変換によって, 点集合は超平面集合に変換されるので, アレンジメント構造は点集合上の関係構造にも対応する. また, 有向マトロイドの線形な表現でもある. アレンジメントのフェイスの数の数え上げや, 実際にその構造を求めることは, 離散・計算幾何の基礎となっており, ゾーン定理や,  -集合に関係するレベルなど種々の有用な定理が知られている.
-集合に関係するレベルなど種々の有用な定理が知られている.
詳説
超平面のアレンジメント(hyperplane arrangement) とは, 超平面による空間の 分割である. 双対変換によって, 点集合は超平面集合に変換されるので, 点集合の問題にも対応する. また, 離散システムの観 点からは, 線形有向マトロイドの1つの表現である. 組合せ幾何とアルゴリズ ムからの詳しい解説が [1] にある.
 次元ユークリッド空間
次元ユークリッド空間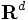 内の
内の 個の超平面(
個の超平面(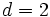 の場合は直線) の集合
の場合は直線) の集合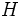 を考える. この
を考える. この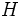 によって,
によって, 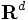 はいろいろな次元のフェイス (face) に分割される. 例えば, 2次元内の有限個の直線の集合は, 2次元, 1次元, 0次元のフェイス (面, 辺, 点) に平面を自然に分割する. これらのフェイスの集合とその接続関係, 各フェイスに対しそれを含む超平面の情報を合わせたものを
はいろいろな次元のフェイス (face) に分割される. 例えば, 2次元内の有限個の直線の集合は, 2次元, 1次元, 0次元のフェイス (面, 辺, 点) に平面を自然に分割する. これらのフェイスの集合とその接続関係, 各フェイスに対しそれを含む超平面の情報を合わせたものを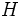 のアレンジメントといい,
のアレンジメントといい, 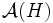 と書く. フェイスの次元を明記したいときは,
と書く. フェイスの次元を明記したいときは,  次元
次元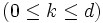 のフェイスを
のフェイスを -フェイスと書く.
-フェイスと書く. 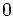 -フェイスを頂点,
-フェイスを頂点, 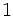 -フェイスを辺,
-フェイスを辺, 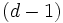 -フェイスを ファセット (facet),
-フェイスを ファセット (facet),  -フェイスをセル (cell) とも呼ぶ.
-フェイスをセル (cell) とも呼ぶ.
フェイス がフェイス
がフェイス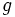 の部分フェイスであるとは,
の部分フェイスであるとは,  の次元が
の次元が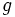 の次元 より1だけ小さく,
の次元 より1だけ小さく,  が
が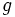 の境界に含まれていることである.
の境界に含まれていることである.  が
が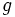 の部 分フェイスならば,
の部 分フェイスならば,  と
と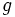 は (互いに) 接続しているといい, この関係 を接続関係という. フェイスの接続関係全体は束をなし, アレンジメントは, 各フェイスの座標など幾何情報と, このフェイスのなす束で表される.
は (互いに) 接続しているといい, この関係 を接続関係という. フェイスの接続関係全体は束をなし, アレンジメントは, 各フェイスの座標など幾何情報と, このフェイスのなす束で表される.
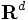 内の
内の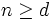 個の超平面のアレンジメントが単純 (simple) である とは,
個の超平面のアレンジメントが単純 (simple) である とは, 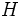 に属する任意の
に属する任意の 個の超平面は1点で交わり, どの
個の超平面は1点で交わり, どの 個の超平面 も共通の交点をもたないことである. アレンジメントの
個の超平面 も共通の交点をもたないことである. アレンジメントの -フェイスの最大数
-フェイスの最大数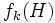 は, アレンジメントが単純であるとき達成され,
は, アレンジメントが単純であるとき達成され,
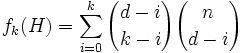
で与えられる. 特に,  -フェイス, すなわちセルの数は
-フェイス, すなわちセルの数は を定数とみなすと
を定数とみなすと 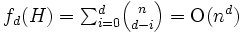 となる.
となる.
アレンジメントは逐次添加法で構成できる. 超平面を1つずつ付け加え, アレンジメントの接続関係を更新していく方法である. 2次元の場合で, 平面上の 本の直線からなる単純なアレンジメントを構成する方法を述べる.
本の直線からなる単純なアレンジメントを構成する方法を述べる.  本の直線の集合を
本の直線の集合を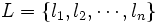 とし,
とし, 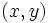 平面上にあるとする.
平面上にあるとする. 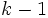 本の直線
本の直線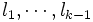 からなるアレンジメントに
からなるアレンジメントに 番目の 直線
番目の 直線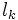 を加えてアレンジメントを更新する. 各頂点には, この頂点に接続している4つの辺を反時計回りの 順で貯えておく. 各辺には, その辺を含む直線の式と辺の両端点の頂点を覚えておく.
を加えてアレンジメントを更新する. 各頂点には, この頂点に接続している4つの辺を反時計回りの 順で貯えておく. 各辺には, その辺を含む直線の式と辺の両端点の頂点を覚えておく. 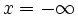 で
で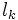 のすぐ上にある直線を左から辿り, この辺の下に接続している面の境界を時計回りに回って行く.
のすぐ上にある直線を左から辿り, この辺の下に接続している面の境界を時計回りに回って行く. 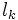 と交わった時は, その交点から始めて, 今度は隣の面の境界 を時計回りに辿る. これを
と交わった時は, その交点から始めて, 今度は隣の面の境界 を時計回りに辿る. これを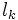 がすでにアレンジメントに存在していた
がすでにアレンジメントに存在していた 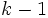 本の直線と交わるまで行なう. この操作により,
本の直線と交わるまで行なう. この操作により, 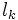 上に新たに現れる頂点もすべて列挙することができ, そこでアレンジメントを更新していくことができる. その手間は, 直線
上に新たに現れる頂点もすべて列挙することができ, そこでアレンジメントを更新していくことができる. その手間は, 直線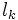 と交わる面の境界上で 辿る辺の数に比例する.
と交わる面の境界上で 辿る辺の数に比例する.
 次元の
次元の 個の超平面のアレンジメントにおいて, 新たに1つ超平面
個の超平面のアレンジメントにおいて, 新たに1つ超平面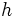 を加え,
を加え, 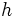 と交わる各セルのフェイスの集合をゾーンと定義すると, 次のゾーン定理が成り立つ.
と交わる各セルのフェイスの集合をゾーンと定義すると, 次のゾーン定理が成り立つ.
ゾーン定理.  次元空間内の
次元空間内の 個の超平面から成るアレンジメントにおいて, 1つの超平面のゾーンのフェイスの総数は
個の超平面から成るアレンジメントにおいて, 1つの超平面のゾーンのフェイスの総数は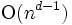 である.
である.
このゾーン定理より, アレンジメントを逐次添加法で構成したときの計算量を 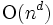 でおさえることができる.
でおさえることができる.
ゾーン定理の離散幾何への応用を1つ上げておく.  次元の
次元の 超平面のアレンジメントのセルの集合を
超平面のアレンジメントのセルの集合を 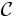 , 各セル
, 各セル のファセットの数を
のファセットの数を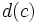 としたとき,
としたとき, 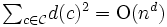 が成り立つ.
が成り立つ. 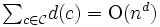 であるから, 各セルのファセットの数はそんなに分散が大きくないことが わかる. 2次元の場合には, このような関係から複数のセルの辺の数を評価することができる.
であるから, 各セルのファセットの数はそんなに分散が大きくないことが わかる. 2次元の場合には, このような関係から複数のセルの辺の数を評価することができる.
 次元超平面アレンジメントにおいて,
次元超平面アレンジメントにおいて, 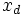 軸に平行な直線で貫いたときに下から
軸に平行な直線で貫いたときに下から 番目となる交点をもつフェイス全体の集合を
番目となる交点をもつフェイス全体の集合を -レベル, または単にレベル という. 2次元の場合, 高々
-レベル, または単にレベル という. 2次元の場合, 高々 までのレベルのサイズは
までのレベルのサイズは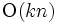 であり,
であり,  -レベルのサイズは
-レベルのサイズは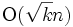 となる. 双対性より, これは平面の
となる. 双対性より, これは平面の 点を直線で等分割する方法の数が
点を直線で等分割する方法の数が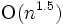 であることも 意味する.
であることも 意味する.  -レベルを
-レベルを 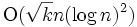 時間で求める 平面走査法アルゴリズムが知られている.
時間で求める 平面走査法アルゴリズムが知られている.
3次元の平面のアレンジメントでもレベルのサイズは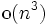 である. 4次元以上の 場合, 全体より小さいオーダであるかどうかはわかっていない. また, 高次元の場合 は, 0, 1次元フェイスの頂点, 辺で構成されるスケルトンをたどるアルゴリズムも知られており, 特に3次元ではアレンジメント全体を 求めるよりも効率よく計算できる. レベルや1つのセルのスケルトンも 有用で, 点集合の問題を双対変 換して解いている場合, スケルトンのみで十分な場合もある.
である. 4次元以上の 場合, 全体より小さいオーダであるかどうかはわかっていない. また, 高次元の場合 は, 0, 1次元フェイスの頂点, 辺で構成されるスケルトンをたどるアルゴリズムも知られており, 特に3次元ではアレンジメント全体を 求めるよりも効率よく計算できる. レベルや1つのセルのスケルトンも 有用で, 点集合の問題を双対変 換して解いている場合, スケルトンのみで十分な場合もある.
曲線・曲面のアレンジメントも有用であり, このアレンジメントの1つのセルやゾーンの 組合せ複雑度の解析は, Davenport-Schinzel列の理論としてまとめられている. 定数次数の代数曲線のアレンジメントでは, セルのフェイス数は 一般次元で全体のオーダよりほぼ1つ小さな次数の数でおさえられる.
[1] H. Edelsbrunner, Algorithms in Combinatorial Geometry, Springer-Verlag, 1987. 邦訳 (今井浩, 今井桂子訳), 『組合せ幾何学のアルゴリズム』, 共立出版, 1995.
- あれんじめんとのページへのリンク
