バケット法
【英】：bucket method
概要
幾何的な問題をより単純に高速に処理するための実際的方法である. 対象物が2次元の
点からなる図形のときは, 対象物を座標軸に平行な辺からなる長方形で覆い, それを縦横
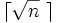等分し全部で
個のバケットと呼ばれる小長方形領域に分割して図形を各バケットで切り出し管理する. すると問題を各バケット内での極めて単純な問題に帰着できることもしばしばあり, 高速に処理できることになる.
詳説
計算幾何の実用的なアルゴリズムの代表的設計法の一つであり, 平面最小重み完全マッチング (matching), 点位置決定 (point location) などがバケット法 (bucket method) に基づいて効率的に解かれている. 簡単のため2次元で説明するが, 高次元にも容易に一般化できる. 平面上にサイズの解きたい問題が与えられたとする. 問題を含む領域を軸に平行な辺からなる長方形で覆い, 軸に垂直な直線を引いて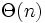
個のバケットと呼ばれる合同な小長方形に分割する. そして全体の問題をそれぞれのバケット内の問題として分割して記憶する. すると通常はバケット内での問題だけで全体の解が得られるので高速になる. バケット間にまたがる情報を必要に応じて利用しなければならない場合もあるがこの場合も高速な手法があることが多い.
具体例でより詳しく説明する. 与えられた平面上の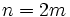
個の点集合に対して, 
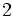点ずつペアにして
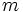個のペアの集合
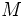をつくるという問題を考える. このような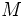は, 完全マッチングと呼ばれている. その際, ペアの重みをそのペアに含まれる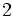点間の距離(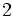点を結ぶ線分の長さ)とする. 完全マッチング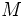の重みを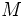に含まれる
個のペアの重みの総和と見なし, 重みを最小にする完全マッチングを求める問題を平面最小重み完全マッチングというが, この問題をバケット法に基づいて解決しその実用性を実証した研究 [2] が, 計算幾何学の問題に対するバケット法の最初の適用例といわれている. できるだけ小さい重みの完全マッチングをつくるわけであるので, 遠く離れた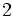点がペアになる可能性は低い. そこで, 対象領域(長方形領域)を縦横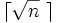等分し全部で
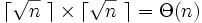個のバケットに分割して, 同一のバケットに含まれる点でまずペアをつくる. 最小重みの完全マッチングには距離の小さい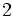点がペアとして含まれることが多いので, 同一のバケットに含まれるもの同士をペアにするということは, 同一のバケットに含まれる2点は極めて近い点である可能性が高く, 異なるバケットに属する2点は遠くにある可能性が高いという, 自然な仮定に基づいている.
このように, バケット法では問題を局所領域に限定できるという特徴がある. さらに, 与えられる点の集合が対象領域において一様に分布するときは, 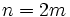個の点に対してほぼ同数個のバケットに分割しているので, 各バケットは平均的に一定数(
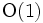)個の点しか含まないといえる. したがって, 各バケット内での最小重み完全マッチングは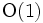の手間で見つけることができる. このように, バケット法では, バケット内の問題が極めて単純であるという特徴も併せもっている. さらに, バケットは合同な長方形であるため, バケットに含まれる点も簡単に求められるという特徴もある. このような特徴から, バケット法に基づく手法は, 一般に極めて高速となる [1].
上の平面最小重み完全マッチングの問題では, バケット内での完全マッチングだけでは, 全体の完全マッチングとはならずに, ペアにされていない点が残るのが普通で, 最終的には, バケット間にまたがる点同士でさらにペアをつくっていかなければならないが, これは, 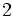次元バケット間の距離を, ある程度忠実に保存するようにして, 一列に並べ, その順番で次々とペアにしていけばよい. このようにして求められた完全マッチングは, 最小重みの完全マッチングでないことが多いが, 詳細な解析により, かなり精度の高い解となることが保証されている [2]. 最適解はネットワークのアルゴリズムを用いて
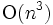の手間で解けるが, 上記のバケット法に基づく方法は
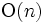の手間であり, 実際の応用では極めて有効である.
平面最小重み完全マッチングをプロッターでペンを用いて地図を描く際の筆順最適化 (optimal drawing (of map) ) に応用する. 地図をきれいに描くため, 同じ線を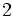度描くことはしないものとする. ペンをおろして線を描いているときもあるし, ペンを上げて次に描くべき線の始まりまで移動しているときもある. 地図を描くという観点からすると, ペンをおろして線を描くという動作は必要不可欠なものである. これに対して, ペンを上げて次に描くべき線の始まりまで移動する動作は, 空送りと呼ばれ無駄な動作であるので, できるだけ少なくするのがよい. さて, 地図が一筆書き可能なら空送りをすることなく描けることになる. 地図が一筆書き不可能ならば空送りの部分に対応する線を付け加えた図で一筆書きできるように変形して描くことになる. プロッターでの描画に要する時間は, ほぼ, この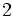つの動作に要する時間の総和になるので, 描画時間を減らすには, 空送り全体に要する時間を減らせばよい. これらの動作に要する時間は移動量に比例するものとすれば, 空送り全体の移動量(移動距離)を最小にすれば, 描画に要する時間は最小ということになる. これは平面最小重み完全マッチングに帰着できる. 地図が一筆書き不可能ならば奇数本の線が接続する点を全部拾ってきて(すると点は偶数個になる), 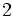個ずつペアにして完全マッチングを求め, 完全マッチングに含まれる線を空送りに対応させて付け加えれば一筆書きできることになる. 完全マッチングの選び方により付け加えた線の総長は異なるので, 総長最小の完全マッチングを求める問題となる.
その他の計算幾何の様々な探索問題に対するバケット法の応用については文献 [1, 3] を参照のこと.
[1] T. Asano, M. Edahiro, H. Imai, M. Iri and K. Murota, "Practical Use of Bucketing Techniques in Computational Geometry," in Computational Geometry, G.T. Toussaint, ed., North-Holland, 1985.
[2] M. Iri, K. Murota and S. Matsui, "Heurisitics for Planar Minimum Weight Perfect Matchings," Networks, 13 (1983), 67-92.
「bucket method」の例文・使い方・用例・文例
- bucket methodのページへのリンク
