待ち行列のバケーションサーバモデル
【英】：queueing model with vacationing server
概要
客がいてもサービスが行なわれない期間(これをサーバのバケーションという)のある待ち行列モデル. 古くは, サーバの稼働制御問題のモデルとして研究され, 近年では, 確率的分解定理と呼ばれる理論的性質と, 通信や生産システムの性能評価への応用が注目されている. 複数の待ち行列を1つのサーバが巡回的にサービスするポーリングモデルも, バケーションサーバモデルとみなすことができる.
詳説
基本的な待ち行列の数多くの変形モデルのうちの1つとして, 客がいるといないとに拘らず, サービスが行なわれない期間 (これをサーバのバケーション (vacation) という) のあるモデルがある. サーバのバケーションがあるモデルは, 伝統的 (1960年代) には, サーバの始動毎に発生する費用と客の待ち時間に対する費用の釣合いを取る最適制御問題として研究された. 1980年以降は, 確率分解定理と呼ばれる興味深い理論的性質と, 通信や生産システムの性能評価のための基礎的理論モデルとしての応用性が注目された. 特に, M/G/1待ち行列のバケーションモデルと, 複数のM/G/ 
待ち行列を1つのサーバが巡回的にサービスするポーリングモデルが活発に研究された [1]. 近年は, 波長分割多元接続光通信方式のモデルに触発されて, サーバがバケーション中にも (稼動期間中とは異なる速さで) サービスを行うというワーキングバケーションモデルが解析されている [2].
サーバのバケーション サーバのバケーションによって表されるものは, 現実のシステムでは, 設備の故障と修理や予防保守の時間の他に, サーバの稼働準備と稼働後処理の時間, 十分な数(あるいは十分な仕事量)が待ち行列に溜るまで稼働開始を遅らせる時間等である. また, 通信方式の性能評価への応用において, 複数のユーザが1つの通信チャネル(サーバ)を時間分割で共有するシステム(例えば, 時分割多元接続やトークンリングLAN) では, 各ユーザにとって, 他のユーザのサービス時間やユーザの切替えに要する時間は, バケーションとみなされる. バケーションのない通常のシステムでも, 待ち行列が空である期間を, 客の到着により直ちに終了するバケーションとみなすことができる.
サーバのバケーションがある待ち行列では, サーバの状態は, 客のサービスを続けて行なう稼働期間と, 上記のような理由によるバケーションの期間が交互に繰り返して現れる. 従って, バケーションモデルは, サーバの稼働期間を終了する規則と, バケーション期間を終了する規則とにより, 分類することができる.
稼働期間を終了する規則 稼働期間を終了する規則には, 稼働開始後に続いてサービスされる客数に対する制限によって, (1)待ち行列が空になるまでサービスを続ける全処理式, (2)稼働開始時点で待ち行列にいた客だけをサービスし, その間に到着する客は, バケーション後の次の稼働期間でサービスするゲート式, 及び(3)一定数(例えば, 1人)の客をサービスするか, または待ち行列が空になるまでサービスを続ける制限式, という3つの基本方式がある.
バケーション期間を終了する規則 バケーション期間を終了する規則には, (1)サーバが1回のバケーションから帰ってきたときに待っている客がいなければ直ちにもう一度バケーションを取るという動作を, バケーション終了時に少なくとも1人の客が待っているようになるまで繰り返す多重バケーションモデル, (2)バケーションは1回だけで, その終了時に待っている客がいなければ, サーバは客が到着すればいつでもサービスを始められる状態で待つ単一バケーションモデル, (3)サーバの始動に要する時間を節約するために, 
人の客が溜るまでサービスを始めない
-方策, 等がある.
確率的分解定理 M/G/1待ち行列 のバケーションモデルにおける興味深い理論的性質として, 確率的分解定理 (stochastic decomposition theorem)について述べる. これは, 適当な条件の下で, バケーションモデルの平衡状態 (equilibrium state)における客数 
の確率分布が, 対応するバケーションのないモデルの平衡状態における客数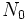 
の確率分布と, バケーション期間のみに依存する客数
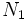の確率分布の畳み込みに分割できるという定理である. 例えば, 多重バケーションモデルの平衡状態における任意時刻の客数について, 分解定理が成り立ち, このとき 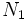はバケーション開始時の客数とバケーション中の任意時刻までに到着する客数の和である. ある場合においては, G/G/1待ち行列のバケーションモデルにおいても分解定理が成り立つ.
さらに, サービスが先着順に行なわれ, バケーションが将来の到着過程に依存しない場合には, 客の待ち時間の分布関数のラプラス・スチルチェス変換に対する同様の分解定理も成り立つ. 例えば, M/G/1待ち行列の全処理式多重バケーションモデルにおいて, 客の平均待ち時間は, ポラチェック・ヒンチンの公式 (Pollaczek-Khintchine formula) として知られるバケーションのない場合の平均待ち時間と, 1回のバケーション時間
の平均前方再生時間 ![\mbox{E} [ V ^2 ] / ( 2 \mbox{E}[V] )\,](https://cdn.weblio.jp/e7/img/dict/orjtn/8c738e9fba2f5c8d5e4ea549ab6c182c.png)
の和で与えられる. 従って, の分散が大きいシステムでは, を一定長だけ延ばすと平均待ち時間が減少するというパラドクスが生じる [3].
ポーリングモデル ポーリングモデル (polling model) とは, 複数の待ち行列を1つのサーバが巡回的にサービスするシステムのことである. サーバが1つの待ち行列から次の待ち行列に移るための移動時間を仮定してもよい. 各待ち行列にとって, 他の待ち行列のサービス時間と移動時間は, サーバのバケーションとみなされる. M/G/ 待ち行列のポーリングモデルについても, 確率的分解定理が成り立つ. これを利用して, すべての待ち行列が同等な場合に, 平均待ち時間の公式が得られる. 各待ち行列のパラメタが異なる一般の場合に, 平均待ち時間を表す公式は得られていない(数値的には計算できる)が, それらにトラヒック強度の重みを付けて加えた量に対する疑似保存則 (quasi-conservation law) が導かれている [4, 5].
[1] H. Takagi, Queueing Analisis: A Foundation of Performance Evaluation, Vols. 1-3, Elsevier, 1991, 1993, 1993.
[2] D.-A.Wu and H.Takagi, "M/G/1 Queue with Multiple Working Vacations," Performance Evaluation, 63 (2006), 654-681.
[3] R. B. Cooper, S. -C. Niu and M. M. Srinivasan, "Some Reflections on the Renewal-Theory Paradox in Queueing Theory," Journal of Applied Mathematics and Stochastic Analysis, 11 (1998), 355-368.
[4] H. Takagi, Analysis of Polling Systems, MIT Press, 1986.
[5] 高木英明, 「ポーリングモデル：巡回サービス多重待ち行列」, 『オペレーションズ・リサーチ』, 41 (1996), 108-118.
| 待ち行列： | 待ち確率 待ち行列 待ち行列のコンピュータへの応用 待ち行列のバケーションサーバモデル 待ち行列の生産システムへの応用 待ち行列の通信への応用 待ち行列ネットワーク |
「queueing model with vacationing server」の例文・使い方・用例・文例
- 社長がエコマーケティングをよく理解していることは、「Do more with less.」という企業理念に現れている。
- 〔人と〕秘密に話し合う, 密談[密議]する 〔with〕.
- 前置詞付きの句, 前置詞句 《in the room, with us など》.
- ête‐à‐tête (with a person) (人と)差し向かいで話す.
- Microsoftがβ版をランチするのは「NetShow streaming server」で動画や音声をオンデマンドで提供する。
- アドバンテージイン 《サーブ側 (server)の得点》.
- queueing model with vacationing serverのページへのリンク
