ホーマン‐きどう〔‐キダウ〕【ホーマン軌道】
ホーマン軌道
最小のエネルギーで到達する「ホーマン軌道」
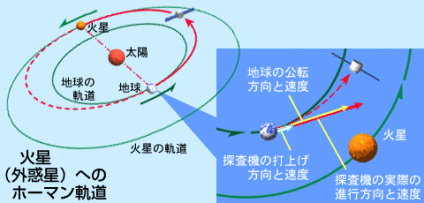
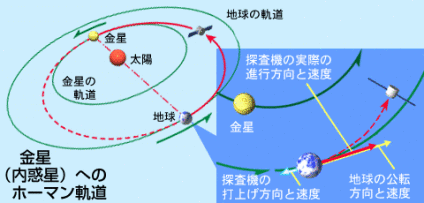
地球から打ち上げられる探査機は、地球の公転速度(秒速約30km)をあらかじめ持っています。地球の公転方向と逆向きに探査機を投入した場合、太陽から見て減速することになり、探査機は地球周辺が遠日点となるようなだ円軌道を周回する人工惑星になります。逆に、地球の公転方向に探査機を投入した場合、太陽から見て加速することになり、探査機は地球周辺が近日点となるようなだ円軌道を周回する人工惑星になります。惑星探査機を打ち上げる場合もこの原理を利用していますが、最小のエネルギーで目的の惑星に到達させる軌道を「ホーマン軌道」といいます。
「ホーマン軌道」より飛行日数が少ない「準ホーマン軌道」
「準ホーマン軌道」は、「ホーマン軌道」に飛ばす場合よりも、速度を上げ、打上げ方向を少しだけ変えたりすることによって、遠日点または近日点に達する前に、目的の惑星と会合し、飛行日数を減らすことができます。現在、ほとんどの惑星探査機は、この方法により打ち上げられています。
火星・金星へのホーマン軌道
ホーマン遷移軌道
(ホーマン軌道 から転送)
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/09/05 17:52 UTC 版)
ホーマン遷移軌道（ホーマンせんいきどう、英語: Hohmann transfer orbit) またはホーマン軌道（ホーマンきどう、英語: Hohmann orbit）とは、同一軌道面にある2つの円軌道の間で、軌道を変更するための遷移軌道である。ドイツのヴァルター・ホーマンが1925年に提案した。
概念
| 宇宙力学 |
|---|
 |
ホーマン遷移軌道は、内側の軌道上に近点が有り、外側の軌道上に遠点が有る楕円軌道である（近点・遠点を参照）。軌道半径の比が約11.94を超えず、同一の軌道面上の2つの円軌道の間の遷移の中で、最少のエネルギーで遷移できる軌道である。また、近点と遠点の2回だけしか速度変化を必要としない。なお、軌道半径の比が約11.94を超える場合には、二重楕円遷移の方がエネルギー効率が高い。
静止トランスファ軌道は、低軌道から静止軌道へのホーマン遷移軌道である。地球において、その静止衛星の軌道投入では、ほとんどが静止トランスファ軌道を使用している。なお、低軌道の軌道面が赤道面と一致している事はまずないため、ホーマン遷移と同時に軌道面の遷移も行う。
惑星探査機では、黄道面および目的地の軌道傾斜角が問題となることや、打ち上げタイミングが会合周期（惑星により0.3年 - 2.2年）に1回しか訪れないため、単純なホーマン遷移軌道を使う事例は少ない。
参考文献
- ホーマン軌道 - 宇宙航空研究開発機構(JAXA) 宇宙情報センター
関連項目
 |
この項目は、天文学（天文学者を含む）や地球以外の天体に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:天体／Portal:天文学）。 |
- ホーマン軌道のページへのリンク
