クライン‐の‐つぼ【クラインの×壺】
クラインの壺
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/11/09 19:19 UTC 版)
|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2015年10月)
|
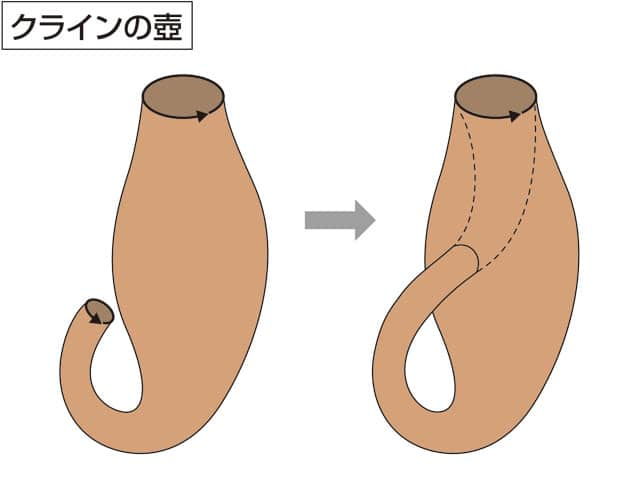
クラインの壺（クラインのつぼ、英: Klein bottle、独: Kleinsche Flasche）は、境界も表裏の区別も持たない（2次元）曲面の一種で、主に位相幾何学で扱われる。
ユークリッド空間に埋め込むには4次元、曲率0とすると5次元が必要である。3次元空間には通常の方法では埋め込み不可能だが、射影して強引に埋め込むと、自己交差する3次元空間内の曲面になる。その形を壺になぞらえたものである。
ドイツの数学者フェリックス・クラインにより考案された。クラインの管、クラインの瓶とも呼ばれる。この通称は英語に翻訳する際の錯誤によるものである。原語であるドイツ語では「Kleinsche Fläche（クラインの面）」であり、これが英語に翻訳される際、Fläche（面）がFlasche（瓶）と取り違えられ、bottleと訳された。現在ではドイツ語圏でも、Kleinsche Flascheのほうで定着している。
クラインの壺は、下図のように矢印を付けた正方形の対辺を矢印の向きが合うように貼り合わせて作ることができる。
前述のように3次元空間内に実現するためには自己交差が必要であるが、クラインの壺そのものに交差はない。そのことを強調するために自己交差の部分をぼかして図示されることがある。
表裏の区別を持たない2次元曲面には他にメビウスの帯がある。メビウスの帯が2次元のテープ状のものをひねり表をたどっていくとそのまま裏に行き着くようにしたのに対し、クラインの壺は3次元のチューブをひねり内部をたどると外部に行き着くようにしたものである。また二つのメビウスの帯をそのふちに沿って貼り合わせるとクラインの壺ができる（上の図で、ここで示した順序とは逆に、青いほうの辺を先に貼り合わせるとメビウスの帯になる）。
関連項目
外部リンク
- Weisstein, Eric W. "Klein Bottle". mathworld.wolfram.com (英語).
- 参考画像
- The Adventures of the Klein Bottle - 小さな壺のアニメーション、壺の中を車で走る。フェリックス・クラインによるオリジナルの描写。ベルリン自由大学での製作。
- トーラス・ゲームズ - 「トーラス」「クラインの壺」「射影平面」のそれぞれで、上下左右が繋がった面上で遊ぶことができるゲーム・ソフト（日本語）。四角形の上下の辺と左右の辺を、向きを揃えてつなげるとトーラスに、片方を逆向きにつなげると（上図参照）クラインの壺になる。どちらも逆向きにすると射影平面になる。
- 浅田彰のクラインの壺をめぐって(山形浩生のウェブページより)
- 浅田彰『構造と力』の《クラインの壺》モデルは間違っていない ～ 一トポロジストの異論 - 数学者の菊池和徳からの反論、2002-03-28
参考文献
- 小笠英志 『異次元への扉―はさみと紙から始めてトポロジーの達人に』 日本評論社 ISBN 978-4535786080 クラインの壺の初心者向けの説明が載っている。
|
この項目は、位相幾何学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:数学／Portal:数学）。 |
クラインの壷
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2018/12/23 04:43 UTC 版)
「マイヤー・ヴィートリス完全系列」の記事における「クラインの壷」の解説
マイヤー・ヴィートリス完全系列のもう少しだけ難しい応用として、クラインの壷 X のホモロジー群の計算を挙げよう。二つのメビウスの帯 A, B をそれらの境界円にそって貼合せた和として X を分解すれば、A, B およびそれらの交わり A ∩ B は円にホモトピー同値であるから、マイヤー・ヴィートリス完全系列の非自明な部分は 0 → H 2 ( X ) → Z → α Z ⊕ Z → H 1 ( X ) → 0 {\displaystyle 0\to H_{2}(X)\to \mathbb {Z} \,{\xrightarrow {\alpha }}\,\mathbb {Z} \oplus \mathbb {Z} \to H_{1}(X)\to 0} となり、かつ自明な部分からは X の次元が 2 以上のホモロジーが消えることがわかる。実際、（メビウスの帯の境界円は中心円の周りを二重に覆うから）真ん中の写像 α は 1 を (2, −2) へ写す。特に α は単射であり、故に 2 以上の次元のホモロジーが消えることが出る。結局、Z2 の基底として (1, 0) および (1, −1) をとれば H ~ n ( X ) ≅ δ 1 n ( Z ⊕ Z 2 ) = { Z ⊕ Z 2 if n = 1 0 if n ≠ 1 {\displaystyle {\tilde {H}}_{n}(X)\cong \delta _{1n}(\mathbb {Z} \oplus \mathbb {Z} _{2})={\begin{cases}\mathbb {Z} \oplus \mathbb {Z} _{2}&{\text{if }}n=1\\0&{\text{if }}n\neq 1\end{cases}}} が得られる。
※この「クラインの壷」の解説は、「マイヤー・ヴィートリス完全系列」の解説の一部です。
「クラインの壷」を含む「マイヤー・ヴィートリス完全系列」の記事については、「マイヤー・ヴィートリス完全系列」の概要を参照ください。
クラインの壷と同じ種類の言葉
- クラインの壷のページへのリンク
