確率密度関数
μ
=
[
0
0
]
,
Σ
=
[
1
3
/
5
3
/
5
2
]
{\displaystyle {\boldsymbol {\mu }}=\left[{\begin{smallmatrix}0\\0\end{smallmatrix}}\right],{\boldsymbol {\Sigma }}=\left[{\begin{smallmatrix}1&3/5\\3/5&2\end{smallmatrix}}\right]}
非退化の場合 多変量正規分布が非退化であるとは、共分散行列
Σ
{\displaystyle {\boldsymbol {\Sigma }}}
[5]
f
X
(
x
1
,
…
,
x
k
)
=
exp
(
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
)
(
2
π
)
k
|
Σ
|
{\displaystyle f_{\mathbf {X} }(x_{1},\ldots ,x_{k})={\frac {\exp \left(-{\frac {1}{2}}({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\right)}{\sqrt {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}}}
ここで
x
{\displaystyle {\mathbf {x} }}
k 次元列ベクトルで、
|
Σ
|
≡
det
Σ
{\displaystyle |{\boldsymbol {\Sigma }}|\equiv \det {\boldsymbol {\Sigma }}}
Σ
{\displaystyle {\boldsymbol {\Sigma }}}
行列式 である。
Σ
{\displaystyle {\boldsymbol {\Sigma }}}
1
×
1
{\displaystyle 1\times 1}
複素正規分布(英語版 ) の場合はこれとはわずかに違った形のものになる。
k+1 次元空間内の任意の「等高線」、つまり確率密度関数の値が等しくなるような点の集合は、楕円 またはその高次元対応物となる。よって多変量正規分布は楕円分布(英語版 ) の特別な場合である。
記述統計量
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
{\displaystyle {\sqrt {({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})}}}
マハラノビス距離 として知られ、試験ベクトル
x
{\displaystyle {\mathbf {x} }}
μ
{\displaystyle {\boldsymbol {\mu }}}
k
=
1
{\displaystyle k=1}
標準得点 の絶対値に帰着する。
2変量の場合 2次元で非退化の場合(k = rank(Σ) = 2[X Y ]′ (右肩のダッシュは転置を表す)の確率密度関数は、
f
(
x
,
y
)
=
1
2
π
σ
X
σ
Y
1
−
ρ
2
exp
(
−
1
2
(
1
−
ρ
2
)
[
(
x
−
μ
X
)
2
σ
X
2
+
(
y
−
μ
Y
)
2
σ
Y
2
−
2
ρ
(
x
−
μ
X
)
(
y
−
μ
Y
)
σ
X
σ
Y
]
)
{\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}+{\frac {(y-\mu _{Y})^{2}}{\sigma _{Y}^{2}}}-{\frac {2\rho (x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right]\right)}
となる。ここで ρ は X と Y の相関係数 であり、
σ
X
>
0
{\displaystyle \sigma _{X}>0}
σ
Y
>
0
{\displaystyle \sigma _{Y}>0}
μ
=
(
μ
X
μ
Y
)
,
Σ
=
(
σ
X
2
ρ
σ
X
σ
Y
ρ
σ
X
σ
Y
σ
Y
2
)
{\displaystyle {\boldsymbol {\mu }}={\begin{pmatrix}\mu _{X}\\\mu _{Y}\end{pmatrix}},\quad {\boldsymbol {\Sigma }}={\begin{pmatrix}\sigma _{X}^{2}&\rho \sigma _{X}\sigma _{Y}\\\rho \sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\end{pmatrix}}}
2次元のときは、多変量正規分布であるための同値な条件として挙げた最初の方は、やや緩められる:
可算無限 通りの X と Y の線型結合がどれも正規分布に従うならば、ベクトル [X Y]′ は2変量正規分布に従う[6]
2変数の場合の等高線を x,y -平面にプロットすると楕円になる。相関係数 ρ が大きくなっていくとき、楕円は次の直線:
y
(
x
)
=
sgn
(
ρ
)
σ
Y
σ
X
(
x
−
μ
X
)
+
μ
Y
.
{\displaystyle y(x)=\operatorname {sgn}(\rho ){\frac {\sigma _{Y}}{\sigma _{X}}}(x-\mu _{X})+\mu _{Y}.}
の方向に向かって押しつぶされていく。この背景として、この式の sgn(ρ ) ("sgn" は符号関数 )を ρ に取り換えたものは、X の値が与えられたときの Y の最良線形不偏予測量(英語版 ) (best linear unbiased prediction)になっているという性質がある[7]
結合分布の正規性 正規分布と独立性 確率変数
X
{\displaystyle X}
Y
{\displaystyle Y}
(
X
,
Y
)
{\displaystyle (X,Y)}
ρ
=
0
{\displaystyle \rho =0}
正規分布に従う確率変数の対は、必ずしも2変量正規分布には従わない 2個の確率変数
X
{\displaystyle X}
Y
{\displaystyle Y}
(
X
,
Y
)
{\displaystyle (X,Y)}
X は標準正規分布(平均 0、分散 1)に従う。ある定数
c
>
0
{\displaystyle c>0}
|
X
|
>
c
{\displaystyle |X|>c}
Y
=
X
{\displaystyle Y=X}
|
X
|
<
c
{\displaystyle |X|<c}
Y
=
−
X
{\displaystyle Y=-X}
3変数以上の場合も同様に反例が構成できる。一般に、こうした確率変数の和によって混合分布モデル(英語版 ) が作られる。
相関と独立性 一般に、2個の確率変数が無相関であっても独立であるとは限らない。しかし、確率変数ベクトルが多変量正規分布に従っている場合、その2個以上の成分が互いに無相関であれば、それらは独立である。特に、これらが組ごとに独立(英語版 ) であれば、独立である。
しかしながら、すぐ上で指摘した例からわかるように、2個の確率変数が正規分布に従い、かつ無相関であるからといって、それらが独立であるとは限らない(X と Y の相関係数が 0 となるよう定数 c を選べばよい)。
周辺分布 多変量正規分布に従う確率変数ベクトルから、その中のいくつかの成分を抜き出した確率変数の組が従う周辺分布を得るには、単に平均ベクトル、分散共分散行列から無関係な成分を除けばよい。これが成り立つことは、多変量正規分布の定義と線形代数によって証明できる[8]
例 X = [X 1 , X 2 , X 3 ]μ = [μ 1 , μ 2 , μ 3 ]Σ とする。 このとき X′ = [X 1 , X 3 ]μ′ = [μ 1 , μ 3 ]
Σ
′
=
[
Σ
11
Σ
13
Σ
31
Σ
33
]
{\displaystyle {\boldsymbol {\Sigma }}'={\begin{bmatrix}{\boldsymbol {\Sigma }}_{11}&{\boldsymbol {\Sigma }}_{13}\\{\boldsymbol {\Sigma }}_{31}&{\boldsymbol {\Sigma }}_{33}\end{bmatrix}}}
である。
アフィン変換
X
∼
N
(
μ
,
Σ
)
{\displaystyle \mathbf {X} \ \sim {\mathcal {N}}({\boldsymbol {\mu }},{\boldsymbol {\Sigma }})}
Y = c + BX アフィン変換 であるとき(c は
M
×
1
{\displaystyle M\times 1}
B は
M
×
N
{\displaystyle M\times N}
Y も多変量正規分布に従い、平均ベクトルは c + Bμ BΣB T である(つまり
Y
∼
N
(
c
+
B
μ
,
B
Σ
B
T
)
{\displaystyle \mathbf {Y} \sim {\mathcal {N}}\left(\mathbf {c} +\mathbf {B} {\boldsymbol {\mu }},\mathbf {B} {\boldsymbol {\Sigma }}\mathbf {B} ^{\rm {T}}\right)}
特に、成分 Xi たちの任意の部分集合が従う周辺分布は再び多変量正規分布になる。例えば、部分集合 (X 1 , X 2 , X 4 )T を直接抜き出してくるには、行列
B
=
[
1
0
0
0
0
…
0
0
1
0
0
0
…
0
0
0
0
1
0
…
0
]
{\displaystyle \mathbf {B} ={\begin{bmatrix}1&0&0&0&0&\ldots &0\\0&1&0&0&0&\ldots &0\\0&0&0&1&0&\ldots &0\end{bmatrix}}}
を使えばよい。
別の系として、多変量正規分布に従う X と定ベクトル b のドット積 をとった Z = b · X
Z
∼
N
(
b
⋅
μ
,
b
T
Σ
b
)
{\displaystyle Z\sim {\mathcal {N}}\left(\mathbf {b} \cdot {\boldsymbol {\mu }},\mathbf {b} ^{\rm {T}}{\boldsymbol {\Sigma }}\mathbf {b} \right)}
B
=
[
b
1
b
2
…
b
n
]
=
b
T
{\displaystyle \mathbf {B} ={\begin{bmatrix}b_{1}&b_{2}&\ldots &b_{n}\end{bmatrix}}=\mathbf {b} ^{\rm {T}}}
と考えればよい。Σ の正定値性(半正定値性)から、ドット積をとった確率変数の分散は正(非負)になる。
X のアフィン変換 2X は、X と同一の分布に従う2個の独立な確率変数の和とは別物である。
母数の推定 確率密度関数が
f
(
x
)
=
1
(
2
π
)
k
|
Σ
|
exp
(
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
)
{\displaystyle f(\mathbf {x} )={\frac {1}{\sqrt {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}}\exp \left(-{1 \over 2}(\mathbf {x} -{\boldsymbol {\mu }})^{\rm {T}}{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\right)}
である多変量正規分布に従う大きさ n の標本から、共分散行列を推定することを考える。この場合の最尤推定量 は
Σ
^
=
1
n
∑
i
=
1
n
(
x
i
−
x
¯
)
(
x
i
−
x
¯
)
T
{\displaystyle {\widehat {\boldsymbol {\Sigma }}}={1 \over n}\sum _{i=1}^{n}({\mathbf {x} }_{i}-{\overline {\mathbf {x} }})({\mathbf {x} }_{i}-{\overline {\mathbf {x} }})^{\rm {T}}}
であり、これは単純に標本共分散行列を計算したものである。ただし不偏推定量 ではなく、期待値は
E
[
Σ
^
]
=
n
−
1
n
Σ
{\displaystyle E[{\widehat {\boldsymbol {\Sigma }}}]={\frac {n-1}{n}}{\boldsymbol {\Sigma }}}
となる。よって
Σ
^
=
1
n
−
1
∑
i
=
1
n
(
x
i
−
x
¯
)
(
x
i
−
x
¯
)
T
{\displaystyle {\widehat {\boldsymbol {\Sigma }}}={1 \over n-1}\sum _{i=1}^{n}(\mathbf {x} _{i}-{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})^{\rm {T}}}
とすれば不偏推定量になる。多変量正規分布の母数の推定において、フィッシャー情報行列 は閉じた式で書け、例えばクラメール・ラオの限界 の算出に用いられる。詳細はフィッシャー情報量 を参照。
多変量正規分布からのサンプリング 平均ベクトル μ 、分散共分散行列 Σ の N 次元正規分布に従う乱数ベクトルを生成する方法として、以下に述べるような手法が広く用いられている[9]
A A T = Σ A をどれか1つ見つける。Σ が正定値の場合はコレスキー分解 が典型的に用いられるが、(平方根演算を避けた)拡張法は Σ が半正定値であれば必ず通用し、いずれの方法でも適当な行列 A が得られる。別の方法として、Σ のスペクトル分解 Σ = UΛU −1 を用いて A = UΛ ½ としてもよい。前者は計算論的に率直な手法だが、分布の基となる確率変数の並べ替え(Σ の行・列交換)によって行列 A は異なったものに変化する。一方後者は、このような変換をしても A の成分が並べ直されるだけである。理論上はどちらの手法を使っても行列が同程度に良く求まるが、計算時間には違いが出る。z = (z 1 , …, zN )T N 個の独立な確率変数から成るベクトルとする(このような乱数は例えばボックス=ミュラー法 によって得られる)。x を μ + Az 関連項目 脚注
^ a b c Lapidoth, Amos (2009). A Foundation in Digital Communication . Cambridge University Press. ISBN 978-0-521-19395-5
^ Gut, Allan (2009). An Intermediate Course in Probability . Springer.
ISBN 978-1-441-90161-3 ^ Kac, M. (1939). “On a characterization of the normal distribution”. American Journal of Mathematics 61 (3): 726–728. doi :10.2307/2371328 . JSTOR 2371328 . ^ Sinz, Fabian; Gerwinn, Sebastian; Bethge, Matthias (2009). “Characterization of the p-generalized normal distribution”. Journal of Multivariate Analysis 100 (5): 817–820. doi :10.1016/j.jmva.2008.07.006 . ^ UIUC, Lecture 21. The Multivariate Normal Distribution , 21.5:"Finding the Density".^ Hamedani, G. G.; Tata, M. N. (1975). “On the determination of the bivariate normal distribution from distributions of linear combinations of the variables”. The American Mathematical Monthly 82 (9): 913–915. doi :10.2307/2318494 . JSTOR 2318494 . ^ Wyatt, John. “Linear least mean-squared error estimation ”. Lecture notes course on applied probability . 2012年1月23日 閲覧。 ^ 周辺分布についての正式な証明は http://fourier.eng.hmc.edu/e161/lectures/gaussianprocess/node7.html 参照。 ^ Gentle, J.E. (2009). Computational Statistics doi :10.1007/978-0-387-98144-4 .
ISBN 978-0-387-98143-7 . http://cds.cern.ch/record/1639470
参考文献
離散単変量で
離散単変量で
連続単変量で
連続単変量で
連続単変量で
連続単変量で
混連続-離散単変量
多変量 (結合)
方向
退化 と特異
族
サンプリング法(英語版 )
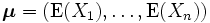 , (
, (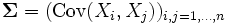 とすると,
とすると, 
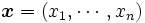 として
として
![f(\boldsymbol{x})=
\displaystyle{\frac{1}{(2\pi)^{n/2} \sqrt{|\mathbf{\Sigma}|}} \mathrm{exp}
\left[ - \frac{1}{2}
(\boldsymbol{x}-\boldsymbol{\mu}) \mathbf{\Sigma}^{-1}
(\boldsymbol{x}-\boldsymbol{\mu})^{\top} \right] }
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/4587d779f18c0d90d03b5039f68dfb9d.png)
 は
は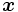 の
の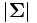 は
は









![{\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}+{\frac {(y-\mu _{Y})^{2}}{\sigma _{Y}^{2}}}-{\frac {2\rho (x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fca42ffd6e6daf34cbe42d814acd3c353a826c8f)























![{\displaystyle E[{\widehat {\boldsymbol {\Sigma }}}]={\frac {n-1}{n}}{\boldsymbol {\Sigma }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74699060ed25bc094b5c1d4e183f50484eafc46d)



