カルマン‐フィルター【Kalman filter】
カルマンフィルター
【英】:Kalman filter
概要
(1) 信号を生成するシステムのモデル, (2) 雑音の統計的性質,(3) 初期状態に関する事前情報の3つが与えられたとき, 観測データから状態ベクトルの最小2乗推定値を逐次的に生成するオンラインアルゴリズムである. カルマンフィルターの応用は航空宇宙工学, 制御工学, 通信工学, OR, 土木工学など, 非常に広範な分野にわたっている.
詳説
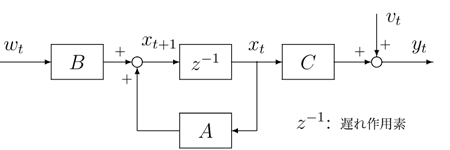 |
| 図1:状態空間モデル |
図1に示すガウス白色雑音を受ける離散時間線形確率システムを考える.
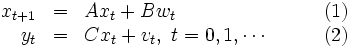
ただし, 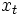 はn次元状態ベクトル,
はn次元状態ベクトル, 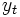 はp次元観測ベクトル,
はp次元観測ベクトル, ,
, 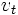 は
は および
および 次元ガウス白色雑音ベクトルで, 平均値は0, 共分散行列は
次元ガウス白色雑音ベクトルで, 平均値は0, 共分散行列は
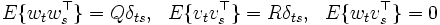
であるとする. ただし,  ,
, 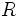 は非負定値対称行列,
は非負定値対称行列, 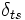 はクロネッカーの記号である.
はクロネッカーの記号である. 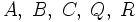 は一般に時間の関数であってもよいが,簡単のために添字
は一般に時間の関数であってもよいが,簡単のために添字 は省略している. また初期値
は省略している. また初期値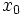 は平均値
は平均値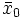 ,共分散行列
,共分散行列 のガウス確率ベクトルであり, 雑音とは無相関であるとする.
のガウス確率ベクトルであり, 雑音とは無相関であるとする.
カルマンフィルタは, 観測データ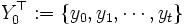 に基づいて,状態
に基づいて,状態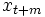 の最小分散推定値(すなわち
の最小分散推定値(すなわち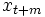 の条件付き期待値)
の条件付き期待値)
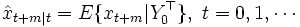
を逐次的に計算するアルゴリズムである. 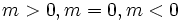 にしたがってそれぞれ, 予測, 濾波, 平滑という.以下では, 状態ベクトルの予測推定値, 濾波推定値を
にしたがってそれぞれ, 予測, 濾波, 平滑という.以下では, 状態ベクトルの予測推定値, 濾波推定値を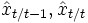 と表し, それぞれの推定誤差共分散行列を次のようにおく.
と表し, それぞれの推定誤差共分散行列を次のようにおく.
![P_{t/t-1}=E\{[x_t-\hat{x}_{t/t-1}][x_t-\hat{x}_{t/t-1}]^{\top}\}, \quad
P_{t/t}=E\{[x_t-\hat{x}_{t/t}][x_t-\hat{x}_{t/t}]^{\top}\}
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/dc1689809bb3d5a3dfad14d907249416.png)
1960-61年にカルマン(R. E. Kalman)と ビュシー(R. S. Bucy)は式(1), (2)の状態空間モデルに対して, カルマンフィルターと呼ばれる以下のようなアルゴリズムを提案した [1, 2, 3, 4, 5, 6].
![\begin{array}{rlll}
\hat{x}_{t+1/t}&=&A\hat{x}_{t/t}, \quad \hat{x}_0=\bar{x}_0 & \qquad (3)\\
\hat{x}_{t/t}&=&\hat{x}_{t/t-1}+K_t[y_t-C\hat{x}_{t/t-1}] & \qquad (4)
\end{array}
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/8a551d225eba2565e8552409dbbf4b95.png)
(ii) カルマンゲイン
![K_t=P_{t/t-1}C^{\top}[CP_{t/t-1}C^{\top}+R]^{-1} \qquad (5)
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/cba6335549c973be747e72271a1ced38.png)
![\begin{array}{rlll}
P_{t+1/t} &=& AP_{t/t}A^{\top} + BQB^{\top} & \qquad (6)\\
P_{t/t} &=& P_{t/t-1}-P_{t/t-1}C^{\top}[CP_{t/t-1}C^{\top}+R]^{-1}CP_{t/t-1},
\quad P_{0/-1}=\Sigma_0 & \qquad (7)
\end{array}
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/8a21a7aa43e767219c71389dc58aa860.png)
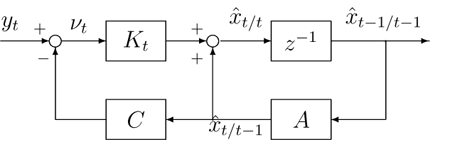 |
| 図2:カルマンフィルターのブロック線図 |
図2にカルマンフィルタのブロック線図を示す.カルマンフィルタは観測値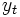 を入力とし, 推定値
を入力とし, 推定値 ,
, 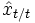 を逐次的に出力する線形動的システムであり,
を逐次的に出力する線形動的システムであり,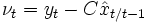 はイノベーションと呼ばれている.
はイノベーションと呼ばれている.
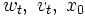 がガウス分布でない場合には, 上のアルゴリズムは状態ベクトルおよび信号の線形最小分散推定値を与えるという意味で, 最適なフィルタである.
がガウス分布でない場合には, 上のアルゴリズムは状態ベクトルおよび信号の線形最小分散推定値を与えるという意味で, 最適なフィルタである.
式(6), (7)から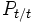 を消去して,
を消去して,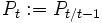 とおくと, 離散時間リッカチ方程式
とおくと, 離散時間リッカチ方程式
![P_{t+1}=A(P_{t}-P_{t}C^{\top}[CP_{t}C^{\top}+R]^{-1}CP_{t})A^{\top} + BQB^{\top} \qquad (8)
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/6301aa568bc33ad77fff27c905626328.png)
を得る. また上式の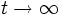 における極限を代数リッカチ方程式という. 制御理論の分野には(代数)リッカチ方程式に関する膨大な研究がある [7].
における極限を代数リッカチ方程式という. 制御理論の分野には(代数)リッカチ方程式に関する膨大な研究がある [7].
白色雑音を受ける非線形確率システムに対しても,その線形化モデルにカルマンフィルタを適用することができるので, カルマンフィルタは航空宇宙工学の分野において飛翔体の軌道推定に威力を発揮した. また状態ベクトルだけてなく, モデルに含まれる未知パラメータを同時に推定する拡張カルマンフィルタも提案されており, カルマンフィルタの応用は時系列の推定を始めとして非常に多くの分野に見られる.
[1] R. E. Kalman, "A New Approach to Linear Filtering and Prediction Problem," Transactions of American Society of Mechanical Engineers, Journal of Basic Engineering, 82D (1960), 34-45.
[2] R. E. Kalman and R. S. Bucy, "New Results in Linear Filtering and Prediction Theory," Transactions of American Society of Mechanical Engineers, Journal of Basic Engineering, 83D (1961), 95-108.
[3] B. D. O. Anderson and J. B. Moore, Optimal Filtering, Prentice-Hall, 1979.
[4] M. S. Grewal and A. P. Andrews, Kalman Filtering - Theory and Practice, Prentice-Hall, 1993.
[5] 有本 卓, 『カルマンフィルター』, 産業図書, 1977.
[6] 片山 徹, 『新版応用カルマンフィルタ』, 朝倉書店, 2000.
[7] S. Bittanti, A. J. Laub and J. C. Willems (Eds.), The Riccati Equation, Springer, 1991.
- かるまんふぃるたーのページへのリンク
