投票理論
【英】：voting theory
概要
投票は集団が意思決定をする場合の1つの手段である. 集団が合理的な意思決定をするためには, どのような投票方法を採用すべきか, しかも矛盾がなく, 必ず結論が得られ, 不平等が生じないというような合理的な投票方法は存在するのか, といった問題が投票理論の主要課題である. このような問題は数百年にわたって多くの哲学者, 経済学者, 政治学者, 数学者等によって考えられてきた.
詳説
投票は集団の意思決定の一つの手段である. 集団が合理的な意思決定をするためには, どのような投票方法を採用すべきか, しかも矛盾がなく, 必ず結論が得られ, 不平等が生じないというような合理的な投票方法は存在するのか, という問題が投票理論の主要課題である. 個人の投票に基づく選択結果を集計する際, 各票を等価と見なした上で多数決にしたがうというのが多数決ルールであるが, 多数決ルールには投票のパラドックスと呼ばれる困難な現象が伴う. 経済学者アロー(K. J. Arrow)は合理的な投票方法を探るため, 個人の投票に基づく選択結果を集計し, 集団の意思決定をする場合の公理主義的なアプローチを提案した. すなわちアローは, 集団の合理的な意思決定のためのルールが満たすべき条件として, 以下の(i) - (v)の5条件を提起した.
(i) 普遍性条件 : 投票者のすべての選好のパターンを集計できるような決定でなければならない.
(ii) 全員一致条件 : 投票者の間に不一致がない場合, 集団の決定もそれと合致しなければならない.
(iii) 一対決定条件 : 一対の選択肢ごとの集団の決定は個々の投票者の決定のみに依存する.
(iv) 完全性条件 : すべての選択肢に対して選好順位が決定されなければならない.
(v) 推移律条件 : 任意の3つの選択肢X, Y, Zに対して, XがYより選好され, YがZより選好されるならば, XはZより選好される.
アローは上記の(i) - (v)の5条件を満たすのは, 個人が選択肢につけた選好順位がそのまま集団の選好順位になるという独裁制以外には存在しないことを示した. これをアローの不可能性定理と呼ぶ. そこでアローは第6の条件として非独裁制を提起し, これら6つのすべてを満たす合理的な意思決定ルールが存在しないことを証明した.
一対比較は一対の選択肢のどちらを選好するかを比較するという操作を繰り返すことによって全体の順位をつける方法である. この中でも, 多数決ルールの場合と同様に, 複数の選択対象の間に投票のパラドックスに基づく循環現象が生じる. 投票方法として最も一般的なものは多数決投票である.
個の選択対象の中から
(
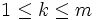)個を選ぶための投票としてのヘア投票は
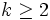の場合の選挙に対して提案されたものであるが, もちろん
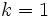の時にも使用できる. 任意のの値に対して, ヘア投票法では各投票者は1からまでの順位付けを行う. 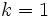の場合, ある選択肢が投票者の過半数によって第1位に順位付けされる場合には, その選択肢が当選する. そうでない場合には, 第1順位の得票数が最小の選択肢をすべての投票者の順位付けリストから除去し, 各投票者は
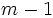個の選択肢の順位付けを得ることになる. そして除去された選択肢を第1順位に順序付けした投票者達は, 新しい第1順位の選択肢を持つことになる. このようにして得られた新たな順位付けにおいて, ある選択肢が投票者の過半数によって第1位に順位付けされる場合には, その選択肢を当選とする. もしそうでなければ, 上の手続きを繰り返し, 第1回目の手続きで残った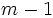個の選択肢の順位付けにおいて第1順位の獲得票数が最小のものを除去し, この2回目の除去に伴って再び新たな
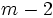個の選択肢の順位付けを得る. この手続きをいずれかの選択肢が第1順位の投票の過半数を獲得するまで続ける.
個のチームがそれぞれの相手と一定回数だけ試合を行なうというリーグ戦の結果に基づいて順位をつける場合を考えてみよう. このようにすべての2つのチームの間で一方が勝ち, 負け, あるいは引き分けという形の結果が得られ, それを基に全体としての順位をつけるというのが, 一対比較による順位付けである. 最も一般的な方法は各チームの勝率に基づくものである.
[1] W. F. Lucas(ed.), Modules in Applied Mathematics, Springer-Verlag, 1983.
[2] S. M. Pollock, M. H. Rothkopf and A. Barnett, Operations Research and the Public Sector, in Handbooks in Operations Research and Management Science, North-Holland, Amsterdam, Netherland, 1994. (大山達雄監修翻訳,『公共政策ORハンドブック』, 朝倉書店, 741pp., 1998.)
投票理論
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2018/03/29 21:43 UTC 版)
投票理論は投票の方式に関する数学である。現在では社会選択理論の一部として扱われることが多い。離散数学の組合せ論の考え方が多く使われる。
問題は大きく分けて2つある。
問題のひとつは、与えられた状況下で、できるだけ最適な投票の方式を見つけることである。よく知られているものには、絶対多数決方式と相対多数決方式などがある。あまり知られていないかもしれないが、ボルダ統計方式、コンドルセ・ウィナー方式などもある。このように多くの投票方式が存在する。ただし、これらの投票の方式は、必要十分条件を考えれば、起こりうる状況すべてで最適とは言えないだろう。
もうひとつの問題は、投票方式の各票の重みに関するものである。1人の人が複数の投票をできるような場合（例えば株式会社の中の株主）が該当する。投票する人の実際の力に対するその人の投票数を測るのに使われたりする。その人の持つ投票の力を示す指数としてシャープレイ＝シュービック投票力指数やバンザフ指数などがある。
例
ある会社で3人の株主がそれぞれ 4票、3票、2票、の投票権を持つとする。 つまり、それぞれの人の投票には4、3、2の重みがついている。投票する人の実際の力が正確に反映されるかを考える。 絶対多数決で、議題が採用されるのには必ず5票以上必要となる。そのため投票で勝つためには少なくと2人以上の人に投票され なければならない。勝つための組み合せは、(4,3)、(4,2)、(3,2)、(4,3,2)である。それぞれの人の投票の力を適切にはかる上で、 勝つための組み合せが重要である。それぞれの人に対して、勝つ組合せの中で、その人の投票によって負ける状況に変わるものの数を数える。 この数のことを、 バンザフ指数という。 したがって、4票を持つ株主の場合、（4,3) と (4,2) から4票を取ると総票が5票未満になるので、負けることになる。 よって、4票を持つ株主のバンザフ指数は2である。同様にして3票と2票を持つ株主のバンザフ指標も2である。 4票を持つ人は2票の人の2倍の票数を持っているが、彼らは同じ投票の力である。
- 投票理論のページへのリンク
