大域的最適化
【英】:global optimization
概要
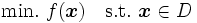
において  か
か 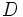 の一方, あるいは両方が凸でなければ, 一般に値の異なる複数の局所的最適解が存在する. その中から大域的最適解, つまり
の一方, あるいは両方が凸でなければ, 一般に値の異なる複数の局所的最適解が存在する. その中から大域的最適解, つまり
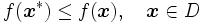
詳説
ユークリッド空間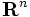 上で定義された連続な実数値関数
上で定義された連続な実数値関数 を目的関数とし,
を目的関数とし,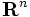 の閉部分集合
の閉部分集合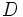 を実行可能集合とする最適化問題:
を実行可能集合とする最適化問題:
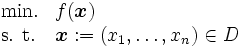 |
|
|
を満足する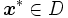 を求める方法を大域的最適化という.目的関数
を求める方法を大域的最適化という.目的関数 と実行可能集合
と実行可能集合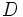 が共に凸性を満たす凸計画問題であれば,局所的な最適化によって
が共に凸性を満たす凸計画問題であれば,局所的な最適化によって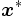 を求めることができる.また,凸性を満たさなくとも,分数計画問題(fractional programming problem)や幾何計画問題(geometric programming problem)の一部は任意の局所的最適解で大域的にも最適となる.したがって,大域的最適化が本質的な意味をもつのは,目的関数値が異なる複数の局所的最適解をもつ非凸計画問題に対してであり,これを多極値大域的最適化問題(multiextremal global optimization problem)と呼ぶ.例えば,
を求めることができる.また,凸性を満たさなくとも,分数計画問題(fractional programming problem)や幾何計画問題(geometric programming problem)の一部は任意の局所的最適解で大域的にも最適となる.したがって,大域的最適化が本質的な意味をもつのは,目的関数値が異なる複数の局所的最適解をもつ非凸計画問題に対してであり,これを多極値大域的最適化問題(multiextremal global optimization problem)と呼ぶ.例えば, が凹関数で
が凹関数で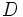 が凸多面体の凹最小化問題(concave minimization problem)の場合,局所的最適解は一般に
が凸多面体の凹最小化問題(concave minimization problem)の場合,局所的最適解は一般に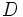 の複数の端点に現われる.しかし,端点の数は膨大であり,その中から大域的に最適なものを見つけだすのは容易な作業でない.実際,この単純な例でさえ最悪計算量の上ではNP困難であることが知られている.そのため,現段階で一般の多極値大域的最適化問題を解決する有効な手段はなく,モンテカルロ法(Monte Carlo method)などのヒューリスティクスが唯一現実的なアプローチとなっている [2].
の複数の端点に現われる.しかし,端点の数は膨大であり,その中から大域的に最適なものを見つけだすのは容易な作業でない.実際,この単純な例でさえ最悪計算量の上ではNP困難であることが知られている.そのため,現段階で一般の多極値大域的最適化問題を解決する有効な手段はなく,モンテカルロ法(Monte Carlo method)などのヒューリスティクスが唯一現実的なアプローチとなっている [2].
このように困難な問題クラスではあるが,個々の問題の中には,その構造を利用することで現実的な計算時間のうちに大域的最適解の求められるものも少なくない [1].その代表例が,実は上にも述べた凹最小化問題である:
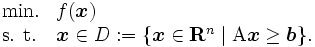
|
ここで,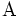 は
は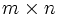 行列で
行列で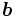 は
は 次ベクトル,
次ベクトル, は凹関数(concave function),つまり
は凹関数(concave function),つまり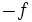 が凸関数である.この非凸計画問題を大域的に最適化するアルゴリズムとして,凹性カット法(concavity-cut method),外部近似法(outer approximation method),分枝限定法(branch-and-bound method)などがある [3].
が凸関数である.この非凸計画問題を大域的に最適化するアルゴリズムとして,凹性カット法(concavity-cut method),外部近似法(outer approximation method),分枝限定法(branch-and-bound method)などがある [3].
凹性カット法は,以下の操作を繰り返し,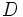 から大域的最適解以外の実行可能解をすべて除去しようとする方法である.局所的最適解を与える
から大域的最適解以外の実行可能解をすべて除去しようとする方法である.局所的最適解を与える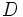 の端点
の端点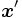 を見つけ,
を見つけ,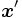 から出る
から出る 本の稜線ベクトル
本の稜線ベクトル と,それまでに得られた最も小さな目的関数値
と,それまでに得られた最も小さな目的関数値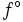 によって集合
によって集合
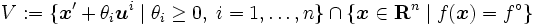 |
を定義する.端点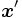 における
における の値が
の値が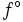 よりも悪ければ,
よりも悪ければ, は丁度
は丁度 個の点から構成されるが,それらを通る
個の点から構成されるが,それらを通る 次元超平面によって
次元超平面によって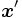 と一緒に見込のない実行可能解も
と一緒に見込のない実行可能解も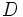 から切除する.目的関数
から切除する.目的関数 が2次の凹関数である双線形計画問題 (bilinear programming problem)に対しては,より大きな領域を切除する方法も考案されている.
が2次の凹関数である双線形計画問題 (bilinear programming problem)に対しては,より大きな領域を切除する方法も考案されている.
外部近似法も超平面による切除を行うが,凹性カット法と違って実行可能解は1つも失わない.まず,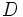 を
を 次元単体や矩形などの単純な凸多面体
次元単体や矩形などの単純な凸多面体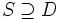 で近似し,
で近似し, を
を 上で最小化する.これも凹最小化問題であるが,
上で最小化する.これも凹最小化問題であるが, は端点の数が少ないので,それらの列挙で最小点
は端点の数が少ないので,それらの列挙で最小点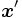 は比較的容易に求められる.この
は比較的容易に求められる.この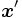 が満たさない
が満たさない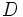 の制約式の1つ
の制約式の1つ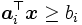 を選び,
を選び, を
を
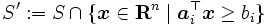 |
に更新して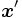 と共に実行不可能な領域を切除する.実行可能集合
と共に実行不可能な領域を切除する.実行可能集合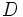 が
が の部分集合なので
の部分集合なので は大域的最適値の下界値を与えるが,以上の操作を繰り返して
は大域的最適値の下界値を与えるが,以上の操作を繰り返して 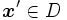 となれば,
となれば,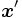 が大域的最適解である.
が大域的最適解である.
分枝限定法には多くのバリエーションが存在するが,最も効力を発揮するのは目的関数 が1変数凹関数
が1変数凹関数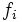 の和に分離可能な場合である:
の和に分離可能な場合である:
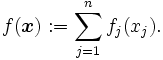 |
|
|
に分割していく.基本となる操作は,組合せ最適化問題に使われる分枝限定法と同様で,まず 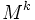 を選んで
を選んで
限定操作  上における
上における の下界値
の下界値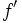 を計算し,その値がそれまでに得られた最も小さな目的関数値
を計算し,その値がそれまでに得られた最も小さな目的関数値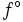 以上ならば
以上ならば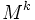 を考察の対象から外す;
を考察の対象から外す;
を繰り返す.効率の鍵を握る下界値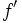 には,通常
には,通常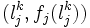 と
と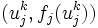 を通るアフィン関数
を通るアフィン関数
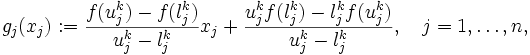 |
を定義し,その和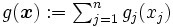 の
の 上における最小値が用いられる.関数
上における最小値が用いられる.関数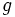 は
は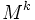 上における
上における の最も大きな下界値を与える凸関数で,凸包絡関数 (convex envelope function)と呼ばれる.しかし,アフィン関数であるので単体法や内点法を使って容易に最小値
の最も大きな下界値を与える凸関数で,凸包絡関数 (convex envelope function)と呼ばれる.しかし,アフィン関数であるので単体法や内点法を使って容易に最小値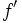 を計算することができる.
を計算することができる.
DC計画問題(d.c. programming problem)や逆凸計画問題(reverse convex programming problem)などのより一般的な多極値大域的最適化問題も,凹最小化問題を逐次解くことで処理することができる [2, 3].
[1] H. Konno, P.T. Thach and H. Tuy, Optimization on Low Rank Nonconvex Structures, Kluwer Academic Publishers, 1997.
[2] R. Horst and P.M. Pardalos (eds.), Handbook of Global Optimization, Kluwer Academic Publishers, 1995.
[3] R. Horst and H. Tuy, Global Optimization - Deterministic Approaches, 3rd ed., Springer-Verlag, 1996.
大域的最適化と同じ種類の言葉
- 大域的最適化のページへのリンク
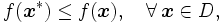
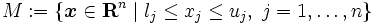 を
を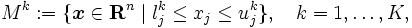
 ならば,
ならば, ,
,  に
に