二元配置分散分析--各水準の繰返し数が等しく，1 である場合
例題：
「表 1 のようなデータがある。4 種の肥料間で収量に差があるか，また，3 種の品種ごとに差があるか検定しなさい。」
| 肥料 | ||||
|---|---|---|---|---|
| 品種 | B1 | B2 | B3 | B4 |
| A1 | 9 | 17 | 12 | 16 |
| A2 | 1 | 21 | 16 | 11 |
| A3 | 7 | 19 | 6 | 9 |
検定手順:
- 前提
- 帰無仮説 H0：「要因効果がない」。
- 対立仮説 H1：「要因効果がある」。
- 有意水準 α で両側検定を行う（片側検定は定義できない）。
注：意味的に両側検定である。形式的には F 分布の片側確率を使う片側検定である。
- 各セルの測定値を Xij（ i = 1， 2， ... ， a；j = 1， 2， ... ， b ）とする。
例題では，a = 3，b = 4 である。
- 分析対象変数 X の全変動 SSt は以下のように 3 個の独立な変動に分解できる。
全変動 = 要因 A の効果 + 要因 B の効果 + 残差
SSt = SSa + SSb + SSe
SSa と SSb はそれぞれ要因 A，要因 B の主効果とよばれる。この場合には交互作用はない。これは，乱塊法に他ならない。
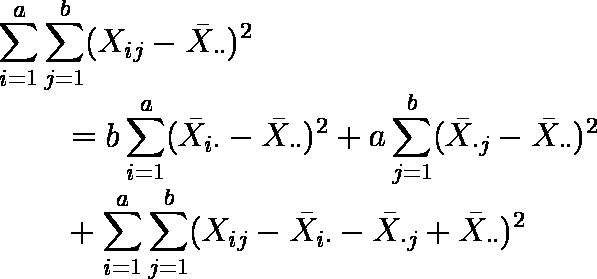
- 二元配置分散分析の結果は，表 2 のような分散分析表で表される。
表 2．分散分析表 - 1 変動要因 平方和 自由度 平均平方 F値 要因 A SSa dfa=a-1 MSa=SSa/dfa Fa=MSa/MSe 要因 B SSb dfb=b-1 MSb=SSb/dfb Fb=MSb/MSe 残差 SSe dfe=(a-1)(b-1) MSe=SSe/dfe 全体 SSt dft=ab-1
例題では，表 3 のようになる。表 3．例題に対する分散分析表 要因 平方和 自由度 平均平方 F 値 有意確率 品種 21.50000 2 10.75000 0.6592845 0.55103 肥料 268.6667 3 89.55556 5.492334 0.03719 残差 97.83333 6 16.30556 合計 388.0000 11 35.27273
- 要因 A の有意性の検定は，Fa が第 1 自由度が dfa，第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 B の有意性の検定は，Fb が第 1 自由度が dfb，第 2 自由度が dfe である F 分布に従うことを利用する。
- それぞれの自由度を持つ F 分布において，有意確率を P = Pr｛F ≧ F0｝ とする。
F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布の上側確率の計算を参照すること。
例題では，品種の差については，自由度が（2，6）の F 分布において，Pr｛F ≧ 5.14｝= 0.05 であるから，P = Pr｛F ≧ 0.659｝＞ 0.05 である（正確な有意確率：P = 0.551）。
肥料の差については，自由度が（3，6）の F 分布において，Pr｛F ≧ 4.76｝= 0.05 であるから，P = Pr｛F ≧ 5.492｝＜ 0.05 である（正確な有意確率：P = 0.037）。
- 帰無仮説の採否を決める。
例題では，有意水準 5% で検定を行うとすれば（α = 0.05），品種の差においては P ＞ α であるから，帰無仮説を採択する。すなわち，「品種の差があるとはいえない」とする。肥料の差においては P ＜ α であるから，帰無仮説を棄却する。すなわち，「肥料の差がある」とする。
「1 である場合」の例文・使い方・用例・文例
- 1歳の娘は英語を多少は話すことができます
- 午後10時ごろ帰って来ます
- 約1か月のあいだ雨が降った
- 4人横1列になって歩く
- 数字の13が不運をもたらすと信じるのはばかげている
- 「happy」という語ではアクセントは第1音節にある
- スペードの1
- 彼は最高のピアニストの1人だと認められている
- 100エーカーのコーヒー農園
- 一律10パーセントの賃上げ
- あの家は家族が1人増えた
- この切符は1枚で2人入れます
- 18歳未満の子どもはこの映画は見られません
- このホールは1,200人収容できる
- 科学的知識は16世紀以来大いに進歩してきた
- 医者は1週間の休養をとるようにと強く勧めた
- この夏は休暇を1週間とれそうだ
- ５時15分過ぎです
- その絵を買った10年後，それが偽物だとわかった
- さらに私はもう1つ問題をかかえている
Weblio日本語例文用例辞書はプログラムで機械的に例文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。
- 1である場合のページへのリンク
