待ち行列モデル M/G/1
【英】:queueing model M/G/1
概要
客の到着がポアソン過程にしたがい, サービス時間が, 一般分布にしたがう窓口1個(扱い者1人)の無限長の待ち行列を許す最も基本的な待ち行列モデルの1つ. M/G/1 型の待ち行列は, M/G/1モデルから派生する種々の待ち行列を指し, 例えば有限待合室モデル(M/G/1/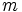 ), 有限呼源モデル (M(
), 有限呼源モデル (M(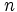 )/G/1), 休暇時間を伴う待ち行列(バケーションモデル M/G/1 +Vacation)などがある.
)/G/1), 休暇時間を伴う待ち行列(バケーションモデル M/G/1 +Vacation)などがある.
詳説
待ち行列モデル M/G/1 (queueing model M/G/1) は, 客の到着が到着率 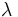 のポアソン過程に従い, サービス時間が一般分布
のポアソン過程に従い, サービス時間が一般分布 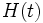 に従う, 窓口1個 (扱い者1人) の無限長の待ち行列を許す最も基本的なモデルである.
に従う, 窓口1個 (扱い者1人) の無限長の待ち行列を許す最も基本的なモデルである.
客の到着間隔 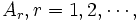 およびサービス時間
およびサービス時間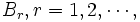 は互いに独立で,
は互いに独立で, 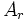 は平均
は平均 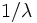 の指数分布,
の指数分布, 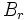 はサービス時間分布
はサービス時間分布 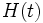 に従う. したがって任意の時間帯
に従う. したがって任意の時間帯 ![(\tau, \tau+t ]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/e55f6dfe0a3cceed2628759784deba8d.png) における到着客数
における到着客数 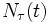 は, 平均
は, 平均 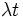 のポアソン分布に従う確率変数となる. 客のサービス規律として, 通常, 先着順 (FCFS) を仮定するが, 後着順 (LCFS), ランダム順 (ROS) などのサービス規律を考えることもある.
のポアソン分布に従う確率変数となる. 客のサービス規律として, 通常, 先着順 (FCFS) を仮定するが, 後着順 (LCFS), ランダム順 (ROS) などのサービス規律を考えることもある.
先着順サービスの M/G/1 モデルでは, 平均サービス時間を 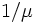 とすると, 利用率
とすると, 利用率 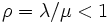 のときにシステムは安定となり, 時間の経過とともに平衡状態へ近づく. 平衡状態における客の待ち時間分布
のときにシステムは安定となり, 時間の経過とともに平衡状態へ近づく. 平衡状態における客の待ち時間分布 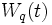 はポラチェック・ヒンチンの公式 (Pollaczek-Khintchine formula)
はポラチェック・ヒンチンの公式 (Pollaczek-Khintchine formula)
![W_q^*(s) = (1-\rho)/ \{1-\lambda[1-H^*(s)]/s\}
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/ee445c13581b568f4abb6feb678044d5.png)
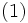
によって与えられる. ここで  はそれぞれ
はそれぞれ 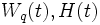 のラプラス・スチルチェス変換である.
のラプラス・スチルチェス変換である.
平均待ち時間 式 (1) から, 平衡状態における平均待ち時間 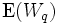 は,
は, 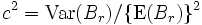 をサービス時間分布の変動係数として,
をサービス時間分布の変動係数として,
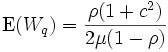
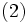
で与えられることが分かる. この式から平均行列長, 平均系内人数, 平均系内滞在時間などはリトルの公式を用いて容易に導くことができる.
式 (2) は, 同じ 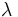 と
と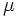 をもった M/M/1 モデルの平均待ち時間を
をもった M/M/1 モデルの平均待ち時間を 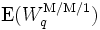 とすれば
とすれば
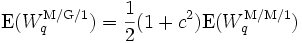
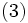
と書ける. これは M/G/1 モデルではサービス時間分布のばらつきが大きいほど長く待たされることを示しており, 最も平均待ち時間が短いのはサービス時間が一定のときで, M/M/1 の 1/2 であることが確かめられる.
M/G/1型待ち行列モデルの解析 以下, M/G/1 モデルとその類似モデルの解析について, いくつかコメントしておこう.
M/G/1 モデルから派生する種々の待ち行列モデルを, M/G/1 型待ち行列モデルと呼ぶ. 例えば, 有限待合室モデル (M/G/1/ ), 有限呼源モデル (M
), 有限呼源モデル (M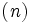 /G/1), 集団到着個別処理モデル (M
/G/1), 集団到着個別処理モデル (M![^{[X]}\,](https://cdn.weblio.jp/e7/img/dict/orjtn/b28ad4df5f9b3ff45b8e9ad2fc83fd6b.png) /G/1), 休暇時間 (準備時間) を伴う待ち行列(バケーションモデル) などはM/G/1 型待ち行列モデルである. また複数個の待ち行列をもつモデル, たとえば多重待ち行列(ポーリングモデル), 優先権のある待ち行列, 移動扱い者によって処理される直列型(網型)の待ち行列などもM/G/1 型待ち行列モデルと考えることができる. M/G/1 モデルの双対的な待ち行列モデルとして, GI/M/1 モデルを考えることもある.
/G/1), 休暇時間 (準備時間) を伴う待ち行列(バケーションモデル) などはM/G/1 型待ち行列モデルである. また複数個の待ち行列をもつモデル, たとえば多重待ち行列(ポーリングモデル), 優先権のある待ち行列, 移動扱い者によって処理される直列型(網型)の待ち行列などもM/G/1 型待ち行列モデルと考えることができる. M/G/1 モデルの双対的な待ち行列モデルとして, GI/M/1 モデルを考えることもある.
M/G/1 モデルやM/G/1 型モデルの常套的な解析法として, 客のサービス終了直後における系内人数に着目する隠れマルコフ連鎖法や, 系内人数の他に残りサービス時間 (あるいはサービス経過時間)を状態変数として取り入れる補助変数法が知られている. また, PASTAが成立するのも特徴の一つである.
待ち行列モデル M/G/1 において, 非割り込みのサービス規律 (先着順, ランダム順など) の下で, 客の退去時点 (サービス終了時点) 直後における系内客数の定常分布  の母関数
の母関数 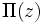 は
は
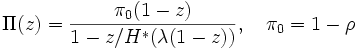
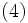
で与えられる. 先着順サービスの下では, ある客 C の系内滞在時間 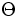 内に到着する客数と C の退去時点の系内客数は等しく, かつ C の系内時間
内に到着する客数と C の退去時点の系内客数は等しく, かつ C の系内時間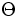 と C の到着以降の到着過程
と C の到着以降の到着過程 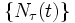 は独立であるから,
は独立であるから, 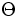 の定常分布
の定常分布 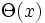 のラプラス・スチルチェス変換を
のラプラス・スチルチェス変換を 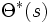 と表せば,
と表せば,
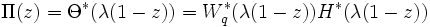
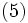
の関係が成立し, 式 (4), (5) より, ポラチェック・ヒンチンの公式 (1) が得られる [1], [3].
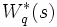 の構造に確率的解釈を与え, 上記のように
の構造に確率的解釈を与え, 上記のように 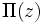 を介さないで直接的に求める手法として, 全稼働期間解析法 (busy period analysis) がある. これは優先権のある待ち行列の解析に有効であり, 各種の全稼働期間中に到着する客の条件付き待ち時間分布のラプラス・スチルチェス変換
を介さないで直接的に求める手法として, 全稼働期間解析法 (busy period analysis) がある. これは優先権のある待ち行列の解析に有効であり, 各種の全稼働期間中に到着する客の条件付き待ち時間分布のラプラス・スチルチェス変換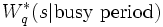 を基本として
を基本として 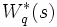 を構成するものである. これによれば
を構成するものである. これによれば
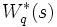 |
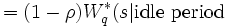 に到着 に到着
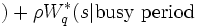 に到着 に到着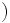 |
![= (1-\rho) \cdot 1 + \rho \cdot R^*(s)
\cdot s(1-\rho)/ \left[ s-\lambda+\lambda H^*(s)
\right]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/7067316672c7431eff0149189b07a42f.png) 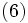 |
となる [1], [3]. ただし 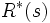 は, 残余サービス時間分布
は, 残余サービス時間分布
![R(t) = \frac{1}{\mathrm{E}(B_r)}
\int_{0}^{t} \left[ 1-H(x) \right] \mathrm{d} x
\ \ \ \ (t \geq 0)
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/697390a42b05778892289919c8efc9a4.png)
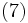
時刻  に仮に客が到着したとすればその客が待たなければならない時間
に仮に客が到着したとすればその客が待たなければならない時間 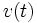 は, 仮り待ち時間 (virtual waiting time) と呼ばれる. 時刻
は, 仮り待ち時間 (virtual waiting time) と呼ばれる. 時刻 における仮り待ち時間の分布関数
における仮り待ち時間の分布関数 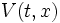 ,
, 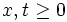 に関して, 次のタカッチの積分-微分方程式 (Tak\'{a}cs' integro-differential equation) が成立する [1].
に関して, 次のタカッチの積分-微分方程式 (Tak\'{a}cs' integro-differential equation) が成立する [1].
![\frac{\partial V(t, x)}{\partial t}
= \frac{\partial V(t, x)}{\partial x}
-\lambda \left[
V(t, x) -\int_{0-}^{x} H(x-y) \mathrm{d}_y V(t, y)
\right]
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/0093413f654c44e7cb8a1be3d93b76d1.png)
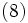
平衡状態 (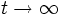 ) における仮り待ち時間の分布関数
) における仮り待ち時間の分布関数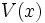 のラプラス・スチルチェス変換
のラプラス・スチルチェス変換 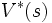 と表わし, 式(8)の左辺を零とおけば、次のレベルクロッシング法[5]の公式 (level-crossing formula) が得られる. これを,
と表わし, 式(8)の左辺を零とおけば、次のレベルクロッシング法[5]の公式 (level-crossing formula) が得られる. これを,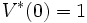 の下に解いて
の下に解いて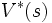 が決定される.
が決定される.
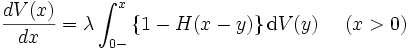
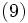
M/G/1 モデルでは PASTA が成立するので 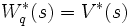 であり, このようにしても式(1) の
であり, このようにしても式(1) の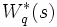 が求められる. さらに, 客の到着が一般分布
が求められる. さらに, 客の到着が一般分布 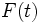 に従う GI/G/1モデルにおけるリンドレーの積分方程式 (Lindley's equation)
に従う GI/G/1モデルにおけるリンドレーの積分方程式 (Lindley's equation)

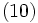
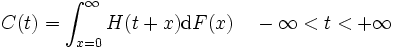
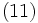
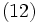
を利用しても 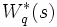 が直接的に求められる [1], [2]. 式 (12) は, M/G/1 における式 (6) の GI/G/1 への一般化であり, さらに一般的な到着過程として定常性のみを仮定した G/G/1 においても成立することが示されている. 本式と
が直接的に求められる [1], [2]. 式 (12) は, M/G/1 における式 (6) の GI/G/1 への一般化であり, さらに一般的な到着過程として定常性のみを仮定した G/G/1 においても成立することが示されている. 本式と 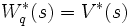 より直ちにポラチェック・ヒンチンの公式を得る.
より直ちにポラチェック・ヒンチンの公式を得る.
なお, 式 (1) の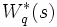 の逆変換形
の逆変換形 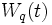 の一つとして次式が知られている.
の一つとして次式が知られている.
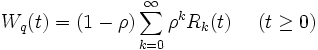
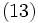
ただし  で,
で, 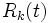 は式 (7) の残余サービス時間分布
は式 (7) の残余サービス時間分布 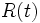 自身の
自身の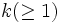 回のたたみこみを表す[1], [4].
回のたたみこみを表す[1], [4].
[1] L. Kleinrock, Queueing Systems Vol. 1: Theory, John Wiley & Sons, 1975.
[2] L. Takács, "The Limiting Distribution of the Virtual Waiting Time and the Queue Size for a Single-Server Queue with Recurrent Input and General Service Times," Sankhya, Series A25 (1963), 91-100.
[3] H. Takagi, Queueing Analysis :A Foundation of Performance Evaluation Vol. 1, Vacation and Priority Systems, Part I, Elsevier Science Publisher B. V., North-Holland, 1991.
[4] N. U. Prabhu, Foundation of Queueing Theory, Kluwer Academic Publishers, 1997.
[5] B. Doshi: Level-crossing Analysis of Queues, Queueing and related models, edited by U. N. Bhat and I. V. Basawa, Oxford University Press (1992), 3-33.
| 待ち行列: | 待ち行列の生産システムへの応用 待ち行列の通信への応用 待ち行列ネットワーク 待ち行列モデル M/G/1 待ち行列モデル M/M/1 待ち行列モデル M/M/c/c 待ち行列モデル M/M/c |
- 待ち行列モデル M/G/1のページへのリンク
![R^*(s) = \mu \left[ 1-H^*(s) \right]/ s \,](https://cdn.weblio.jp/e7/img/dict/orjtn/e50e3304ab6c5441040b7969bfef6ff9.png) で
で