ランダマイゼーション
【英】:randomization
概要
ランダマイゼーションは, アルゴリズムの中にランダムな要素を導入し, それにより最悪の場合にとらわれない簡単で実際に速いアルゴリズムを構成しようという手法である. ランダマイゼーションすることによって得られるアルゴリズムをランダム化アルゴリズムと呼ぶ. ランダマイゼーションは, アルゴリズムに対する入力に確率分布を仮定して計算時間を平均的に評価するとかいうのではない. 代表的な手法に, ランダム抽出法, ランダム順添加法などがある.
詳説
ランダマイゼーション(randomization)は, アルゴリズムの中にランダムな要素を導入し, それにより最悪の場合にとらわれない簡単で実際に速いアルゴリズムを構成しようという手法である. ランダマイザーションすることによって得られるアルゴリズムをランダム化アルゴリズムとよぶ. メタヒューリスティックスのシミュレーティッド・アニーリングから素数判定のランダム化数論アルゴリズムまで幅広く用いられている. ランダマイゼーションは, アルゴリズムに対する入力になんらかの確率分布を仮定して計算時間を平均的に評価するとかいうのではない. 教科書も既にあり, [2] は全般的なアルゴリズムについて, [3] は計算幾何のアルゴリズムについて詳しい.
本項では, 計算幾何の問題に対するランダマイゼーションの代表的手法についてまとめる. 代表的手法としては次の2つのものがあり, 以下その説明をする.
ランダム抽出(random sampling) ランダムに選ぶことにより全体を反映した部分集合を定め, その抽出した部分集合の情報をフルに活用するもの
ランダム順添加法(randomized incremental method) アルゴリズムの構成のもっとも簡単なパラダイムである逐次添加法において, 添加順をランダム化する方法で, 添加法の実用性を示すものでもある.
(a) ランダム抽出 ランダム抽出法の目指すところは, 部分で全体を表すということである. そうできると, 部分を計算するだけで情報がある程度得られるという計算量の観点からの利点がある.
代表的な例で, 平面上の 個の点の集合
個の点の集合 の
の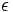 -近似
-近似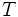 を考える. 任意の
を考える. 任意の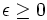 に対して,
に対して,  の部分集合
の部分集合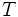 が
が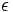 近似である}とは, 任意の半平面
近似である}とは, 任意の半平面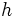 に対して次式が成り立つことをいう.
に対して次式が成り立つことをいう.
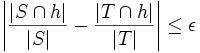
任意の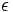 に対して,
に対して, 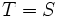 とすればそれは
とすればそれは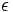 近似になっているから, このような
近似になっているから, このような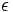 近似の存在は保証されるので,
近似の存在は保証されるので, 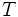 のサイズをどこまで小さくできるかがポイントである. ランダム抽出の理論を適用すると, 次の定理が成り立つ( [1] 参照).
のサイズをどこまで小さくできるかがポイントである. ランダム抽出の理論を適用すると, 次の定理が成り立つ( [1] 参照).
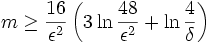
なる 点をランダムかつ独立に選んで得られる集合
点をランダムかつ独立に選んで得られる集合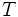 は, 少なくとも
は, 少なくとも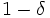 の確率で
の確率で の
の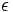 -近似である.
-近似である.
この定理より, 任意の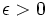 に対して,
に対して, 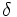 を1に近付けても, ある確率で
を1に近付けても, ある確率で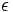 近似が単純なサンプリングで求められということがわかる. 確率が正ならその事象が存在するので, ほぼ定理のサイズの
近似が単純なサンプリングで求められということがわかる. 確率が正ならその事象が存在するので, ほぼ定理のサイズの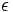 -近似の存在定理も導かれる.
このように
-近似の存在定理も導かれる.
このように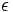 -近似は全体の点数に関係のない点数の部分集合で, 半平面に含まれる点数に関する近似を与えており, 部分によって全体を表現できている. このようなランダム抽出に関する定理は, アルゴリズム構成面で自然と分割統治に使えて有用である. さらに理論の観点からは, 各ニューロンが単純な線形しきい値関数である場合のニューラルネットでの学習能力と関係している.
-近似は全体の点数に関係のない点数の部分集合で, 半平面に含まれる点数に関する近似を与えており, 部分によって全体を表現できている. このようなランダム抽出に関する定理は, アルゴリズム構成面で自然と分割統治に使えて有用である. さらに理論の観点からは, 各ニューロンが単純な線形しきい値関数である場合のニューラルネットでの学習能力と関係している.
(b) ランダム順添加法 ランダム順添加法も有用な方法である. これは, アルゴリズム設計のパラダイムの1つである逐次添加法 (incremental method)をもとにするものである. 従来の逐次添加法は,  要素の問題を解くときに, 最初は定数個(例えば2,3)の要素の部分問題に対する解から始めて,
要素の問題を解くときに, 最初は定数個(例えば2,3)の要素の部分問題に対する解から始めて,  個の要素の部分問題の解があるとき,
個の要素の部分問題の解があるとき,  番目の要素をそこに加えて
番目の要素をそこに加えて 個の要素の部分問題に対する解をつくり, これを
個の要素の部分問題に対する解をつくり, これを 個全体に対する解が得られるまで繰り返す方法である. このとき,
個全体に対する解が得られるまで繰り返す方法である. このとき,  個の要素の部分問題に対する解がわかっていれば, 通常それに1個加えた
個の要素の部分問題に対する解がわかっていれば, 通常それに1個加えた 個の部分問題に対する解は, ゼロからその
個の部分問題に対する解は, ゼロからその 個の問題を解くのに比べて, はるかに効率よく求めることができるということが, 高速アルゴリズムを得るために役立つ. たとえば, 挿入ソートなどは, この典型例である.
個の問題を解くのに比べて, はるかに効率よく求めることができるということが, 高速アルゴリズムを得るために役立つ. たとえば, 挿入ソートなどは, この典型例である.
ランダム順添加法では, ランダマイゼーションにより要素をランダム順に並べ, その順に逐次添加を行なっていく. それによって, 最悪の場合を考えたとき, 単に与えられた順で添加していくと, たいてい逐次添加法にとっては都合の悪い順番が存在し, その場合の計算量が最悪計算時間となってしまうことが多いのに対し, ランダマイゼーションによってそれを避けることができる. これは, 入力になんらかの分布を仮定して平均計算時間を評価するのと近く, ただ複雑な問題では入力の分布として妥当なものを考えることが難しいので, 作為的な入力分布を仮定するより, アルゴリズムの中でランダマイゼーションした方がより汎用的な成果が得られる. また, ランダマイゼーションアルゴリズムといっても, もし, 入力の分布に関して, そう悪い例が出てこなさそうであれば, 実際には単に与えられた順で添加をしていけばよいのである. このランダム順添加法は, 低次元線形計画や凸包構成など幅広く適用されている.
[1] 今井浩, 今井桂子, 『計算幾何学』, 共立出版, 1994.
[2] R. Motwani and P. Raghavan, Randomized Algorithms, Cambridge University Press, 1995.
[3] K. Mulmuley, Computational Geometry: An Introduction Through Randomized Algorithms, Prentice-Hall, 1994.
- ランダマイゼーションのページへのリンク