PID
PID劣化現象
読み方:ピーアイディーれっかげんしょう
別名:PID,PID劣化,PID現象
【英】PID effect
PID劣化現象とは、太陽光発電システムにおいて、特定環境下でソーラーパネル(太陽電池モジュール)の出力が低下する劣化現象である。
PID劣化現象は、回路にかかる高電圧が電位差を生み、電流の漏れを発生させ、出力の大幅な低下を引き起こす現象であると説明される。特に高温多湿の環境に設置され、高電圧がかかるメガソーラーで生じやすいという。必ずしも経年変化・老朽化によるものではなく、設置して間もないシステムでも生じうる。出力低下の度合いは顕著であり、メガソーラーにとって致命的な、対策の急がれる問題とされていた。
PID劣化現象は2000年代半ばに初めて報告され、2010年代になって本格的に問題視されるようになった。産業技術総合研究所(産総研)は2014年3月までにPID劣化現象の原因を特定し、PID劣化現象への耐性を測る試験法を確立、そして長期試験においても劣化現象が見られないCIGSの太陽電池モジュールを開発したと発表した。
参照リンク
PIDによる劣化が起こらないCIGS太陽電池モジュールを開発 - (独立行政法人産業技術総合研究所 2014年3月18日)
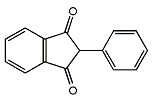
2‐フェニルインダン‐1,3‐ジオン
| 分子式: | C15H10O2 |
| その他の名称: | ジンデバン、ピンジオン、ダニロン、ビンダン、ヘズリン、ジネバル、アトロムボン、ジオフィンダン、フェンヒドレン、フェニリン、インデマ、ジアジラン、Fenilin、Fenhydren、Dineval、Indon、Diadilan、Hedulin、Athrombon、Danilone、Bindan、Dindevan、レクタジオン、Pindione、PID、Rectadione、Diophindane、Indema、Phenindione、フェニンジオン、2-Phenyl-1H-indene-1,3(2H)-dione、2-Phenyl-1,3-indanedione、2-Phenylindane-1,3-dione、2-Phenyl-2,3-dihydro-1H-indene-1,3-dione |
| 体系名: | 2-フェニル-2H-インデン-1,3-ジオン、2-フェニル-1,3-インダンジオン、2-フェニルインダン-1,3-ジオン、2-フェニル-1H-インデン-1,3(2H)-ジオン、2-フェニル-2,3-ジヒドロ-1H-インデン-1,3-ジオン |
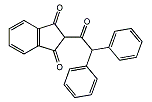
ジファシノン
| 分子式: | C23H16O3 |
| その他の名称: | ソルバン、ジファシン、ジダンジン、ジパキシン、オラグラント、ジファシノン、ジフェナジオン、PID、Solvan、U-1363、Dipaxin、Didandin、Diphacin、Oragulant、Diphacinone、Diphenadione、2-(Diphenylacetyl)indane-1,3-dione、2-(Diphenylacetyl)-1H-indene-1,3(2H)-dione、ジフェナシン、ラチンダン、ラチンダン1、Diphacinon、Ratindan、Ratindan-1、Diphenacin、ダイパキシン、2-(Diphenylacetyl)-1,3-indanedione |
| 体系名: | 2-(ジフェニルアセチル)-1H-インデン-1,3(2H)-ジオン、2-(ジフェニルアセチル)インダン-1,3-ジオン、2-(ジフェニルアセチル)-1,3-インダンジオン |
PID
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/01/30 07:00 UTC 版)
ナビゲーションに移動 検索に移動PID
- プロセス識別子 (Process ID)
- PID制御 (比例: Proportional、積分: Integral、微分: Derivative)
- 単項イデアル整域 (principal ideal domain)
- 骨盤内炎症性疾患 (pelvic inflammatory disease / pelvic inflammatory disorder, PID) 、骨盤内感染症とも
- 電圧誘起出力低下 (Potential-Induced Degradation)
- 工業用設備の配管系統図をPID、またはP&IDと呼ぶ。 (Piping and Instrumentation Diagram 英語版)
- 永続的識別子 (Persistent Identifier)
 |
このページは曖昧さ回避のためのページです。一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。お探しの用語に一番近い記事を選んで下さい。このページへリンクしているページを見つけたら、リンクを適切な項目に張り替えて下さい。 |
PID
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2018/12/14 02:39 UTC 版)
PID上の有限生成加群は PID上の有限生成加群の構造定理によって分類される。準素分解は直既約加群への分解であるので、PID上のすべての有限生成加群は完全直可約である。 明示的に書けば、素イデアル P に対して R/Pn の形の加群(P = 0 を含む、このとき R になる)は直既約である。すべての有限生成 R-加群はこれらの直和である。これが単純であることは n = 1(または P = 0)であることと同値であることに注意せよ。例えば、位数4の巡回群 Z/4Z は直既約であるが単純でない。この群は位数 2 の部分群 2Z/4Z しか非自明な部分群を持たないが、これは直和因子でない。 整数環 Z 上の加群はアーベル群である。有限生成アーベル群が直既約であることとそれが Z か素数 p と正整数 n について Z/pnZ の形の商群と同型であることは同値である。すべての有限生成アーベル群は(有限個の)直既約アーベル群の直和である。 しかしながら、有限生成でない直既約アーベル群が存在する。有理数 Q はその最も単純な例である。 また代数的閉体上の一変数多項式環 K[x] 上の有限生成直既約加群はジョルダン標準形の理論により K[x]/(x − λ)n (λ ∈ K, n ∈ N) に限る。 固定した正整数 n に対し、実数体(または任意の体 K)上の n 次全行列環 R を考える。このとき Kn は(行列の積によるスカラー倍によって)左 R-加群である。これは同型の違いを除いて唯一の直既約 R-加群である。すべての左 R-加群はこの加群 Kn のコピーの(有限か無限の)直和である。
※この「PID」の解説は、「直既約加群」の解説の一部です。
「PID」を含む「直既約加群」の記事については、「直既約加群」の概要を参照ください。
「pid」の例文・使い方・用例・文例
- pidのページへのリンク