最適停止
【英】:optimal stopping
概要
結合分布が既知である確率変数列 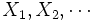 ,と実数値利得関数列
,と実数値利得関数列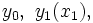
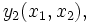
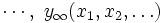 に対して, 逐次に確率変数列
に対して, 逐次に確率変数列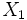 ,
, 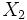 ,
,  を観測し, 各
を観測し, 各 段階において
段階において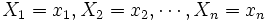 を観測後に観測を停止して利得
を観測後に観測を停止して利得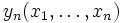 を得るか, 継続して
を得るか, 継続して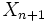 を観測するかを決定を下す.このとき, 期待利得を最大にする(もしくは期待費用を最小化する)停止時刻を求めるのが最適停止問題である.
を観測するかを決定を下す.このとき, 期待利得を最大にする(もしくは期待費用を最小化する)停止時刻を求めるのが最適停止問題である.
詳説
逐次に観測される確率変数列に基づき, 期待利得を最大化したり期待費用を最小化するためにある行動を取る時刻を選ぶ問題を最適停止問題という. 最適停止は次の2つの要素を持つ. (i) 結合分布が既知である確率変数列: 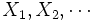 , (ii) 実数値利得関数列:
, (ii) 実数値利得関数列: 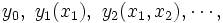
 . 逐次に確率変数列
. 逐次に確率変数列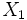 ,
, 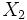 ,
, 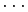 を観測し, 最初の
を観測し, 最初の 段階において
段階において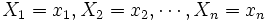 を観測後に観測を停止して利得
を観測後に観測を停止して利得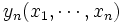 を得るか, 継続して
を得るか, 継続して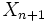 を観測するかの決定を下す. 全く観測しないならば
を観測するかの決定を下す. 全く観測しないならば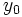 , 決して停止しないならば
, 決して停止しないならば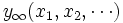 の利得を得る.このとき, 利得を最大にするタイミングである停止時刻を求めるのが最適停止問題である.要素の(ii)は,
の利得を得る.このとき, 利得を最大にするタイミングである停止時刻を求めるのが最適停止問題である.要素の(ii)は,  としたとき, (ii') 結合分布が既知である利得を表す確率変数列:
としたとき, (ii') 結合分布が既知である利得を表す確率変数列: 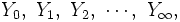 としてもよい. このとき,
としてもよい. このとき, 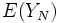 を最大にする停止時刻
を最大にする停止時刻 を求めるのが最適停止問題であるとも記述できる.
を求めるのが最適停止問題であるとも記述できる. 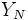 を利得ではなく何らかの費用や損失と解釈すると, 費用ないし損失を最小にする停止規則(時刻)
を利得ではなく何らかの費用や損失と解釈すると, 費用ないし損失を最小にする停止規則(時刻) を求める問題となる.
を求める問題となる.
より一般的には, 最適停止問題は次の様に記述されている. 確率空間 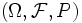 が与えられ,
が与えられ, 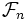 を
を によって生成される
によって生成される 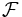 の部分
の部分 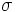 集合,
集合,  を
を 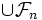 によって生成される
によって生成される 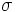 集合とし,
集合とし, 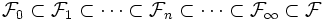 とする. (i)(ii) にかわり(i') 増加部分
とする. (i)(ii) にかわり(i') 増加部分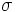 集合列:
集合列: , (ii") 結合分布が既知な利得を表す確率変数列:
, (ii") 結合分布が既知な利得を表す確率変数列: 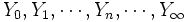 ,とし,
,とし, 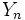 は
は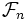 -可測,
-可測, 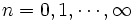 とする.
とする. 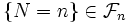 である非負整数値確率変数
である非負整数値確率変数 を停止規則と定義する. (この定義は, いつ停止するかの決定は今までの観測のみに基づき, 将来の観測には基づかないと解釈するとわかりやすい.) このとき
を停止規則と定義する. (この定義は, いつ停止するかの決定は今までの観測のみに基づき, 将来の観測には基づかないと解釈するとわかりやすい.) このとき 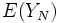 を最大にする停止規則
を最大にする停止規則 を求めるのが最適停止問題である. 一般に全ての最適停止問題を解くことは難しいが, 有限期間問題と単調問題(monotone problem)は解くことができる. 確率変数列
を求めるのが最適停止問題である. 一般に全ての最適停止問題を解くことは難しいが, 有限期間問題と単調問題(monotone problem)は解くことができる. 確率変数列 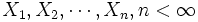 を観測後に必ず停止しなければならないとき, 有限期間問題と呼ぶ.有限期間問題は基本的に後向きの帰納法 (backward induction) によって解かれる.
を観測後に必ず停止しなければならないとき, 有限期間問題と呼ぶ.有限期間問題は基本的に後向きの帰納法 (backward induction) によって解かれる.  期では停止しなければならないので,
期では停止しなければならないので, 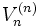 を
を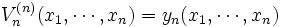 と定義する.
と定義する. 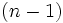 期では, ここで停止したときの利得
期では, ここで停止したときの利得 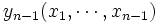 と, 継続して
と, 継続して 期で停止したときの期待利得
期で停止したときの期待利得 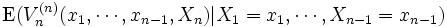 を比較すれば,
を比較すれば, 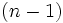 期で停止すべきか継続すべきかが判明する.
期で停止すべきか継続すべきかが判明する.  を次のように定義する.
を次のように定義する. 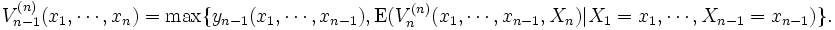 同様に
同様に 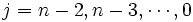 と後ろ向きに
と後ろ向きに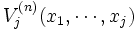 を定義し,
を定義し,
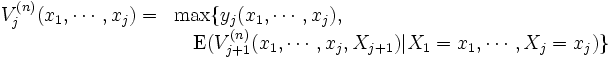
とする. このように定義された 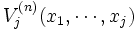 は,
は, 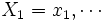 ,
, 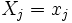 を観測して
を観測して 期から始めたときの最大期待利得を表し, 上式は最適方程式と呼ばれる. これは動的計画の最適性の原理によって得られる関数再帰方程式に他ならず, DP(ダイナミック
期から始めたときの最大期待利得を表し, 上式は最適方程式と呼ばれる. これは動的計画の最適性の原理によって得られる関数再帰方程式に他ならず, DP(ダイナミック プログラミング)方程式とも呼ばれる.
プログラミング)方程式とも呼ばれる.  期においては, 停止して得られる利得
期においては, 停止して得られる利得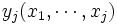 が
が 期より継続して得られる最大期待利得
期より継続して得られる最大期待利得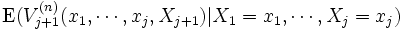 より良ければ停止し, 逆ならば継続するのが良い. それゆえに, 有限期間問題の最適停止規則
より良ければ停止し, 逆ならば継続するのが良い. それゆえに, 有限期間問題の最適停止規則 は, 初めて
は, 初めて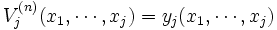 となる
となる で停止することである. 有限期間問題の最大期待利得は,
で停止することである. 有限期間問題の最大期待利得は, 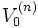 となる.
となる.
最適停止問題において, 事象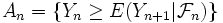 ,
, 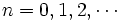 が
が  (almost surely) を満たしているとき単調問題とよぶ. 単調問題では, ある条件の下で([1]参照) OLA (one-stage look-ahead) 停止規則
(almost surely) を満たしているとき単調問題とよぶ. 単調問題では, ある条件の下で([1]参照) OLA (one-stage look-ahead) 停止規則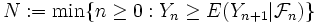 が最適停止規則となる. OLA 停止規則とは, もう1期だけ継続してから停止するよりも, 今停止するほうがよいときに停止することを要求する規則である.
が最適停止規則となる. OLA 停止規則とは, もう1期だけ継続してから停止するよりも, 今停止するほうがよいときに停止することを要求する規則である.
独自のクラスを形成してきたといえる確率最大化最適停止問題に秘書問題がある. 秘書問題は結婚問題とも呼ばれ, 最も基本となる古典的秘書問題は次のように記述される. 1人の秘書を雇いたい. 面接した応募者には同ランクはなくランク付けが可能とする. 1人ずつ面接する毎に, 今までに面接した応募者の相対ランクに基づき採用するか否かを決めなければならず, 一度不採用にした応募者を採用することはできない.  人の応募者があり,
人の応募者があり,  人の面接の順列の一つが実現する確率が
人の面接の順列の一つが実現する確率が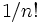 のとき,
のとき,  人中のベストランクを得る確率を最大にする最適停止規則を求めたい. 最適停止規則は,
人中のベストランクを得る確率を最大にする最適停止規則を求めたい. 最適停止規則は, 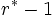 番目までの応募者は全て採用を見送り, それ以降に最初に面接する相対的ベストの応募者を採用しなさい, となり, ここで,
番目までの応募者は全て採用を見送り, それ以降に最初に面接する相対的ベストの応募者を採用しなさい, となり, ここで, 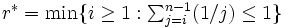 により
により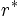 は与えられる.
は与えられる. 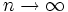 のとき,
のとき,  となる. 大まかに言うと,
となる. 大まかに言うと,  が十分大きいとき, 36.8%まではパスしてそれ以 降に到着する相対的ベストの応募者を採用するのが最適である.
が十分大きいとき, 36.8%まではパスしてそれ以 降に到着する相対的ベストの応募者を採用するのが最適である.
[1] Y. S. Chow, H. Robbins and D. Siegmund, Great Expectations: The Theory of Optimal Stopping, Houghton Mifflin Company, Boston, 1971.
[2] T. S. Ferguson, "Who Solved the Secretary Problem?," Statistical Science, 4 (1989), 282-289.
[3] A. N. Shiryaev, Optimal Stopping Rules, Springer-Verlag, New York, 1978.
[4] J. L. Snell, ""Applications of Martingale System Theorems," Trans. Amer. Math. Soc., 73 (1952), 293-312.
[5] S. M. Ross, Applied Probability Models with Optimization Applications, Holden - Day, San Francisco, 1970.
- 最適停止のページへのリンク
