凸解析
【英】:convex analysis
概要
ベクトル空間における凸集合やベクトル空間上で定義された凸関数の諸性質を取り扱う分野. 最適性理論, 双対性理論, および最適化手法の設計と解析など, 数理計画の様々な事柄に関する基礎理論として非常に重要な役割を果たしている.
詳説
凸解析 (convex analysis) は,ベクトル空間における凸集合あるいはベクトル空間上で定義された凸関数に関する諸性質を取り扱うものであり,数理計画の基礎理論として非常に重要な役割を果たしている.
次の性質をもつ空間 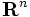 の部分集合
の部分集合 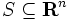 を凸集合 (convex set) と呼ぶ.
を凸集合 (convex set) と呼ぶ.
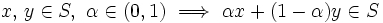
|
特に,有限個の半空間の共通部分として表される凸集合を凸多面体と呼ぶ.
空間 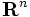 上で定義された拡張実数値関数
上で定義された拡張実数値関数 ![f : \mathbf{R}^n \to [-\infty,+\infty]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/bbfdb48759de85cbf03ff64fd0161c83.png) に対して,そのエピグラフを
に対して,そのエピグラフを と定義し,
と定義し,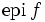 が凸集合であるような関数
が凸集合であるような関数  を凸関数 (convex function) と呼ぶ.ここで,関数
を凸関数 (convex function) と呼ぶ.ここで,関数  の値域に
の値域に 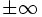 が含まれていることは重要である.考察の対象とする関数をこのように拡張することにより,最適化問題に関連する諸性質を統一的に記述することが可能となる.例えば,実数値凸関数
が含まれていることは重要である.考察の対象とする関数をこのように拡張することにより,最適化問題に関連する諸性質を統一的に記述することが可能となる.例えば,実数値凸関数 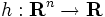 を凸集合
を凸集合 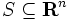 上で最小化する制約つき最適化問題は,拡張実数値関数
上で最小化する制約つき最適化問題は,拡張実数値関数 ![\hat h : \mathbf{R}^n \to (-\infty,+\infty]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/b676f30f6175849323d81ce81f2f115d.png) を
を 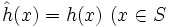 のとき
のとき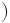 ,
, 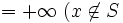 のとき
のとき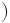 と定義することにより,見かけ上,凸関数
と定義することにより,見かけ上,凸関数 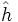 を制約なしで最小化する問題として表すことができる.また,
を制約なしで最小化する問題として表すことができる.また,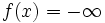 となる点
となる点  が存在せず,さらに恒等的に
が存在せず,さらに恒等的に 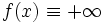 ではないようなものを,特に真凸関数といい,集合
ではないようなものを,特に真凸関数といい,集合 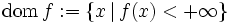 を
を  の実効定義域あるいは単に定義域と呼ぶ.真凸関数は理論的にも実際的にも意味のある凸関数のクラスと考えることができる.なお,
の実効定義域あるいは単に定義域と呼ぶ.真凸関数は理論的にも実際的にも意味のある凸関数のクラスと考えることができる.なお,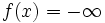 となる
となる  が存在しないような関数
が存在しないような関数  に対しては
に対しては
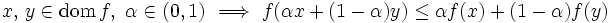
|
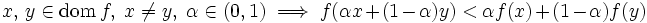
|
であるとき, を狭義凸関数という.明らかに,狭義凸関数は凸関数である.文献 [1,2,3,4,5] に凸関数や凸集合の様々な性質に関する詳しい説明がある.
を狭義凸関数という.明らかに,狭義凸関数は凸関数である.文献 [1,2,3,4,5] に凸関数や凸集合の様々な性質に関する詳しい説明がある.
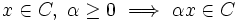 |
特に,凸集合であるような錐を凸錐 (convex cone) という.最適化理論においては,凸錐はしばしば方向ベクトルの集合を表し,特に最適性条件の導出に際して重要である [4].凸錐 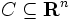 に対して,集合
に対して,集合 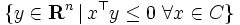 を
を 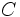 の極錐と呼び,
の極錐と呼び,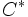 と表す.与えられたベクトル
と表す.与えられたベクトル 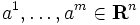 に対して定義される凸錐
に対して定義される凸錐 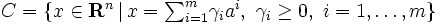 の極錐は
の極錐は 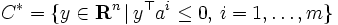 で与えられ,さらに
で与えられ,さらに 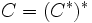 が成り立つ.これは,
が成り立つ.これは,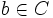 ,すなわち
,すなわち 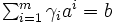 を満たす
を満たす 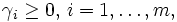 が存在することと,
が存在することと,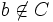 ,すなわち
,すなわち 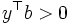 を満たすベクトル
を満たすベクトル 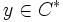 が存在することの,どちらか一方のみが成立することを意味している.これはファーカスの定理と呼ばれている.このように,2つの条件の一方のみが必ず成り立つことを保証する定理は,一般に二者択一定理 (theorem of the alternative) と呼ばれ,最適性条件の導出に有用である [2].
が存在することの,どちらか一方のみが成立することを意味している.これはファーカスの定理と呼ばれている.このように,2つの条件の一方のみが必ず成り立つことを保証する定理は,一般に二者択一定理 (theorem of the alternative) と呼ばれ,最適性条件の導出に有用である [2].
真凸関数  に対して,次式を満足するベクトル
に対して,次式を満足するベクトル 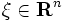 を
を  の
の  における劣勾配 (subgradient) と呼ぶ.
における劣勾配 (subgradient) と呼ぶ.
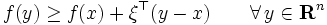
|
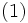 |
真凸関数はその実効定義域 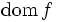 の任意の相対的内点において,少なくとも1つの劣勾配をもつ.特に,凸関数
の任意の相対的内点において,少なくとも1つの劣勾配をもつ.特に,凸関数  が点
が点  において微分可能ならば,
において微分可能ならば, の
の  における劣勾配は唯一存在し,通常の勾配
における劣勾配は唯一存在し,通常の勾配 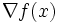 に等しい.しかし,
に等しい.しかし, が点
が点  において微分可能でないときには劣勾配は無数に存在する.一般に,
において微分可能でないときには劣勾配は無数に存在する.一般に, の
の  における劣勾配全体の集合は
における劣勾配全体の集合は 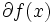 と表される.劣勾配の定義 (1) より,
と表される.劣勾配の定義 (1) より,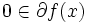 は点
は点  が凸関数の最小点であるための必要十分条件であることは容易に確かめられる.劣勾配の概念は非凸関数に対しても拡張され,微分不可能最適化において基本的な役割を果たしている [1,3,4,5].
が凸関数の最小点であるための必要十分条件であることは容易に確かめられる.劣勾配の概念は非凸関数に対しても拡張され,微分不可能最適化において基本的な役割を果たしている [1,3,4,5].
真凸関数  に対して,次式で定義される真凸関数
に対して,次式で定義される真凸関数 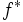 を
を  の共役関数 (conjugate function) という.
の共役関数 (conjugate function) という.
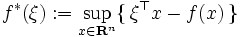
|
 |
いま,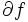 と
と 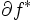 を点-集合写像とみなせば,
を点-集合写像とみなせば,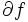 と
と 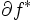 は互いに逆写像の関係にあり,さらに,
は互いに逆写像の関係にあり,さらに,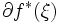 の任意の要素
の任意の要素  は共役関数
は共役関数 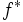 の定義 (2) の右辺の最大を与える.すなわち,次の関係が成立する.
の定義 (2) の右辺の最大を与える.すなわち,次の関係が成立する.
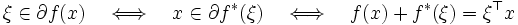
|
共役関数の概念は最適化問題に対する双対理論において特に重要である [3,4,5].
[1] D.P.Bertsekas, Convex analysis and Optimization, Athena Scientific, 2003.
[2] O.L. Mangasarian, Nonlinear Programming, McGraw-Hill, 1969; (reprint, SIAM, 1994).
[3] R.T. Rockafellar, Convex Analysis, Princeton University Press, 1970.
[4] R.T. Rockafellar and R.J.B. Wets, Variational Analysis, Springer, 1998.
- Convex Analysisのページへのリンク
