離散凸解析
【英】:discrete convex analysis
概要
離散的な集合(例えば整数格子点の集合)の上で定義された関数の構造を, 凸解析の視点とマトロイド理論の視点の両方から考察する方法論を, 離散凸解析と呼ぶ. より一般的には, 解析的な視点と組合せ論的な視点の両方から「組合せ論的な凸性」という構造を考察する方法論を指す. 離散最適化, システム解析, 数理経済学などへの応用がある.
詳説
離散的な集合(例えば整数格子点の集合)の上で定義された関数の構造を,凸解析 ([7]) とマトロイド理論 ([1, 8, 9]) の両方の視点から考察する方法論を,離散凸解析 (discrete convex analysis) ([1, 3, 4, 5, 6])と呼ぶ.より一般的には,解析的な視点と組合せ論的な視点の両方から「組合せ論的な凸性」という構造を考察する方法論を指す.離散最適化 ([2, 5]),システム解析 ([6]),数理経済学・ゲーム理論 ([5, 6, 8]),確率過程([5])などへの応用がある. ネットワークフローとの密接な関係も知られている[4, 5, 6].
整数格子点上で定義され整数値をとる関数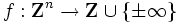 を考える.
を考える.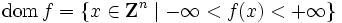 を
を の実効定義域と呼び,以下では,
の実効定義域と呼び,以下では,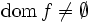 であるような関数だけを考える.
であるような関数だけを考える.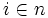 に対してその特性ベクトルを
に対してその特性ベクトルを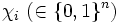 と表わす,すなわち
と表わす,すなわち
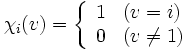
任意の 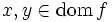 と任意の と任意の 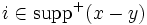 に対して, ある に対して, ある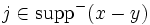 が存在して が存在して
|
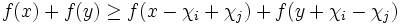
を満たすとき,M凸関数 (M-convex function) という.M凸関数 の実効定義域
の実効定義域 は整基多面体(に含まれる整数格子点)である ([3, 4]参照).
は整基多面体(に含まれる整数格子点)である ([3, 4]参照).
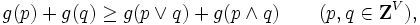
|
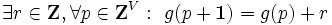
|
を満たすとき,L凸関数 (L-convex function) という.ここで,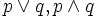 は,それぞれ,成分毎に最大値, 最小値をとって得られるベクトル(すなわち,
は,それぞれ,成分毎に最大値, 最小値をとって得られるベクトル(すなわち,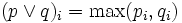 ,
, 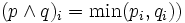 を表し,
を表し, である.L凸関数
である.L凸関数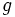 の実効定義域
の実効定義域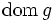 は
は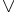 ,
, 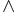 に関して
に関して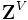 の部分束を成す.また,正斉次L凸関数は,劣モジュラ集合関数と同一視することができる.
の部分束を成す.また,正斉次L凸関数は,劣モジュラ集合関数と同一視することができる.
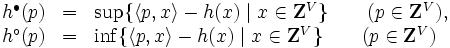
と定義する.ここで,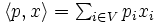 である.この対応
である.この対応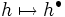 ,
, 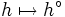 を(凸,凹)離散フェンシェル・ルジャンドル(Fenchel-Legendre)変換と呼ぶ.M凸関数とL凸関数は離散フェンシェル・ルジャンドル変換に関して共役関係にあり,対応
を(凸,凹)離散フェンシェル・ルジャンドル(Fenchel-Legendre)変換と呼ぶ.M凸関数とL凸関数は離散フェンシェル・ルジャンドル変換に関して共役関係にあり,対応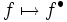 ,
, 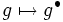 はM凸関数
はM凸関数 とL凸関数
とL凸関数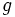 の間の1対1対応を与える.すなわち,M凸関数
の間の1対1対応を与える.すなわち,M凸関数 とL凸関数
とL凸関数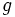 に対して,
に対して,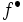 はL凸関数,
はL凸関数, 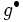 はM凸関数で,
はM凸関数で,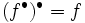 ,
, 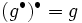 が成り立つ(共役性定理).
が成り立つ(共役性定理).
M凸関数やL凸関数に対して,離散分離定理 (discrete separation theorem) やフェンシェル型双対定理 (Fenchel-type duality theorem) に象徴されるような離散双対性が成り立つ.
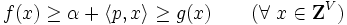
ここで, が整数ベクトルに選べることが離散性の反映である.上の主張で,
が整数ベクトルに選べることが離散性の反映である.上の主張で, をL凸関数,
をL凸関数,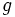 をL凹関数に置き換えたものも成立する(L分離定理).L分離定理は,その特殊ケースとして,劣モジュラ集合関数に関するA. Frankの離散分離定理 ([1] 参照) を含んでいる.
をL凹関数に置き換えたものも成立する(L分離定理).L分離定理は,その特殊ケースとして,劣モジュラ集合関数に関するA. Frankの離散分離定理 ([1] 参照) を含んでいる.
M分離定理とL分離定理は互いに共役の関係にあるが,次に述べるフェンシェル型双対定理は自己共役の形になっている.
- [フェンシェル型双対定理]
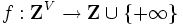 をM凸関数,
をM凸関数,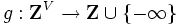 をM凹関数とし,
をM凹関数とし, 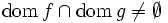 または
または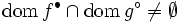 であると仮定する.このとき,
であると仮定する.このとき,
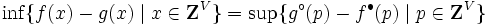
が成り立つ.さらに,この両辺が有限値なら,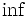 を達成する
を達成する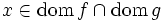 と
と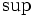 を達成する
を達成する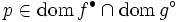 が存在する.
が存在する.
上の定理は,非線形整数計画に関する強双対性を主張しており,その本質的な部分は,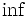 と
と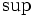 をとる範囲をそれぞれ整数ベクトルに限ってよいという主張にある.
をとる範囲をそれぞれ整数ベクトルに限ってよいという主張にある.
M凸関数,L凸関数の具体的な例,2次のM凸関数,L凸関数の特徴付け,M凸性,L凸性について閉じた基本的な演算については[4, 5, 6] を参照されたい. 特に[5]では,線形代数,組合せ論,距離空間,確率論,オペレーションズリサーチなど,いろいろな文脈で離散凸解析が現れることが紹介されている. M凸関数,L凸関数に関する種々の問題に対して効率的なアルゴリズムが開発されている.これに関しては [4, 6] を参照されたい.
[1] S. Fujishige, Submodular Functions and Optimization,2nd ed., Elsevier, 2005.
[2] N. Katoh and T. Ibaraki, "Resource allocation problems," in Handbook of Combinatorial Optimization, Vol.2, D. -Z. Du and P. M. Pardalos, eds., Kluwer, 159-260, 1998.
[3] K. Murota, "Discrete convex analysis", Mathematical Programming, 83 (1998), 313-371.
[5] 室田一雄, 『離散凸解析の考え方』, 共立出版,2007.
[6] K.Murota, Discrete Convex Analysis, SIAM, 2003.
[7] R. T. Rockafellar, Convex Analysis, Princeton University Press, 1970.
[8] A.Tamura, "Applications of discrete convex analysis to mathmatical economics", Publ. RIMS, 40 (2004) , 1015-1037.
[9] D. J. A. Welsh, Matroid Theory,Academic Press, 1976.
[10] N. White, ed., Theory of Matroids, Cambridge University Press, 1986.
りさんとつかいせきと同じ種類の言葉
- りさんとつかいせきのページへのリンク
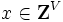
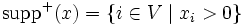 ,
, 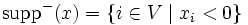 とおく.
とおく.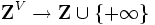 が
が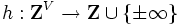 の
の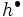 ,凹
,凹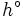 を
を
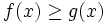
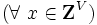 ならば, ある
ならば, ある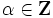 ,
, 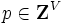 が
が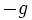 が
が