デリバティブ評価モデル
【英】:no arbitrage pricing model
概要
ある公示性のある指標に対し, 将来時点での支払契約を明示した経済的権利をデリバティブと総称する. さらに将来時点での経済的価値の変動を確率モデルで定式化し, 合理的な資産価格付けが満足すべき性質から, その現在時点での価格を理論的に導出するモデルをデリバティブ評価モデルという. 例えば株式コールオプションでは, 対象とする指標を株価とし, 当該株価を所与の満期時点で, ある一定の行使価格で購入する権利の現在価値を評価する.
詳説
デリバティブ評価モデル(no-arbitrage pricing model) ある公示性のある指標に対し, 将来時点での支払契約を明示した経済的権利をデリバティブという. さらに将来時点での経済的価値の変動を確率モデルで定式化し, 合理的な資産価格付けが満足すべき性質から, その現在時点での価格を理論的に導出するモデルをデリバティブ評価モデルという. 以降では1種類の安全資産と1種類の危険資産が取引されている2証券市場モデルにおける, デリバティブの合理的な価格の導出法について説明する.
まず証券市場においては, 瞬間的な無リスク金利率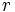 で資産の調達および運用が可能とする. すなわち時点
で資産の調達および運用が可能とする. すなわち時点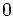 で1円からはじめた預金(もしくは借金)が, 時点
で1円からはじめた預金(もしくは借金)が, 時点 では
では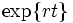 円になるものとする. また1種類の株式が連続的に取引されており, その価格は, 次の確率微分方程式
円になるものとする. また1種類の株式が連続的に取引されており, その価格は, 次の確率微分方程式
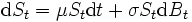
に従うものとする. ただし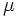 ,
, 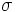 は, ある一定の係数であり,
は, ある一定の係数であり, 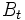 は標準ブラウン運動を表す. このとき将来の一定時点
は標準ブラウン運動を表す. このとき将来の一定時点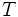 において, 1単位の株式を価格
において, 1単位の株式を価格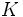 で購入できる権利(これをヨーロピアンタイプのコールオプションという)の, 現在時点
で購入できる権利(これをヨーロピアンタイプのコールオプションという)の, 現在時点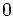 での合理的な現在価値を導出したい.
での合理的な現在価値を導出したい.
いま仮にこのオプションの時点 での価格
での価格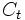 が, 時点
が, 時点 およびその時点での株価
およびその時点での株価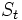 の関数
の関数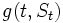 により与えられるとする. このとき伊藤のレンマより,
により与えられるとする. このとき伊藤のレンマより, 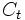 は次の確率微分方程式に従う.
は次の確率微分方程式に従う.
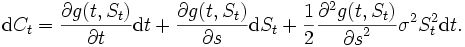
ここで各時点 において, オプションを
において, オプションを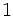 単位保有し, 株式を
単位保有し, 株式を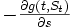 単位保有し, かつ安全資産を
単位保有し, かつ安全資産を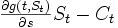 円保有するポートフォリオを考える. ポートフォリオの構成法から, ポートフォリオ全体の価値
円保有するポートフォリオを考える. ポートフォリオの構成法から, ポートフォリオ全体の価値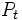 は
は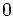 円である. さらにこのポートフォリオの価値変動は, オプションの価値変動と株式の価値変動が相互に不確実な動きを打ち消し合うことにより,
円である. さらにこのポートフォリオの価値変動は, オプションの価値変動と株式の価値変動が相互に不確実な動きを打ち消し合うことにより,
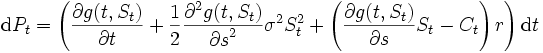
となる. すなわちこのポートフォリオは元手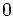 から始めて確実に
から始めて確実に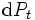 の価値変動をもたらし, もしこの変動が0でなければ, この(もしくは逆の)ポートフォリオにより, リスクを負うことなく確実に儲けることが可能となる. したがってもし証券市場が合理的ならば, このような投資機会は存在しないはずである(これを無裁定条件という). この結果, 合理的なオプション評価額
の価値変動をもたらし, もしこの変動が0でなければ, この(もしくは逆の)ポートフォリオにより, リスクを負うことなく確実に儲けることが可能となる. したがってもし証券市場が合理的ならば, このような投資機会は存在しないはずである(これを無裁定条件という). この結果, 合理的なオプション評価額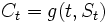 は, 以下の偏微分方程式を満足する必要がある.
は, 以下の偏微分方程式を満足する必要がある.
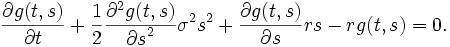
また満期時点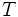 においては, コールオプションの定義から, 以下の境界条件が要求される.
においては, コールオプションの定義から, 以下の境界条件が要求される.
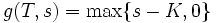 .
.
この2つの条件式から, Black-Scholes モデル[1]におけるB-S公式が導出される.
次にB-S公式によるコールオプション評価額が, 具体的に何を意味しているのかを説明する. 伊藤のレンマを確率積分により表現すると, 以下の関係が成立する.
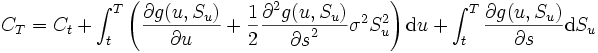
この確率積分の表現に上述の偏微分方程式を代入すると, 結果として次の表現が得られる.
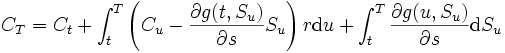
これは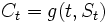 を元手とし, あらたな追加投資をせずに, 各時点
を元手とし, あらたな追加投資をせずに, 各時点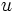 で株式を
で株式を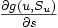 単位保有し, 残りのポートフォリオ価値を安全資産に投資しつづけることにより, 満期時点
単位保有し, 残りのポートフォリオ価値を安全資産に投資しつづけることにより, 満期時点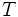 でのポートフォリオ価値が
でのポートフォリオ価値が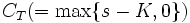 と一致することを示す. すなわちオプションの合理的な評価額とは, 当該オプションの満期時点での価値を複製に必要なポートフォリオの, 現在時点での価値にほかならないのである.
と一致することを示す. すなわちオプションの合理的な評価額とは, 当該オプションの満期時点での価値を複製に必要なポートフォリオの, 現在時点での価値にほかならないのである.
デリバティブの合理的な価格は, その将来時点での経済価値を表す指標が株価以外のさまざまな経済データ(例えば為替, 金利, 天候地震等自然現象)であっても, その根源的リスクへの分割を可能とする証券数が取引されていれば, 同様な考え方によって演繹的に導出可能となる. これが無裁定条件によるオプション評価理論の本質である[2,3].
[1] F. Black and M. Scholes, "The Pricing of Options and Corporate Liabilities," Journal of Political Economy, 81 (1973), 637-659.
[2] J. Cox and S. A. Ross, "The Valuation of Options for Alternative Stochastic Processes," Journal of Financial Economics, 3 (1976), 145-166.
[3] J. M. Harrison and S. R. Pliska, "Martingales and Stochastic Integrals in the Theory of Continuous Trading," Stochastic Processes and Their Applications, 11 (1981), 381-408.
- デリバティブ評価モデルのページへのリンク
