大規模問題の分解法
【英】:decomposition method for large-scale problems
概要
非常に多くの変数や制約条件をもつ最適化問題を, 一部の変数または制約条件だけから成る小さな部分問題の列に変換して解く方法. その多くは, 現実の大規模問題がしばしばもつブロック構造を利用している. 単に大規模問題が実際に解けるようになるだけでなく, もとの問題には見られなかった特徴的な構造が部分問題に現れて, 取り扱いが容易になる場合がある. 特に, 各部分問題が独立に解ける場合には, 並列アルゴリズムを構成する有力な手段となる.
詳説
現実世界で発生する複雑な問題を最適化問題としてモデル化すると,非常に多くの変数や制約条件をもつ大規模問題になることが多い.計算機を用いてその解を求める場合,目的関数や制約条件式がすべて線形であっても,変数や制約条件の数が増えるとともに計算時間は急激に増加する.また,それらの一部に非線形の項が含まれると,問題の解きにくさは飛躍的に増大する.そこで,大規模問題を直接解くのではなく,一部の変数や制約条件だけから成る小規模な,または,解きやすい部分問題を逐次解くことにより,もとの問題の解を得ようとするアルゴリズムが提案されている.それらを一般に大規模問題の分解法 (decomposition method for large-scale problems) と呼ぶ [3].
現実の大規模問題は,しばしば特徴的なブロック構造をもつ.たとえば, 個の比較的独立な部分から成るシステムが共通の変数
個の比較的独立な部分から成るシステムが共通の変数 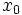 を含む場合は,
を含む場合は,
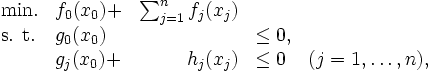 |
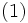 |
という最適化問題が得られる.この問題は,変数 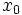 を一時的に固定すると,
を一時的に固定すると,
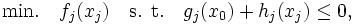
|
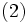 |
という  個の部分問題に分解される.ベンダース分解法 (Benders decomposition method) はこのような性質を利用しており,関数
個の部分問題に分解される.ベンダース分解法 (Benders decomposition method) はこのような性質を利用しており,関数 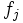 ,
, 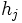 が線形ならば,有限回の反復でもとの問題の解に到達できることが知られている.さらに,分解された部分問題はたがいに独立であり,それらは比較的大きい(粒度が粗い)問題となるため, MIMD (multiple instruction stream multiple data stream) 型の並列計算機で効率よく実行できる.
が線形ならば,有限回の反復でもとの問題の解に到達できることが知られている.さらに,分解された部分問題はたがいに独立であり,それらは比較的大きい(粒度が粗い)問題となるため, MIMD (multiple instruction stream multiple data stream) 型の並列計算機で効率よく実行できる.
また,システム全体にまたがる付加的な制約条件が存在する場合は,
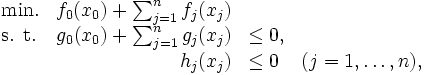
|
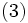 |
という最適化問題が得られるが,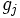 を含む制約条件をラグランジュ緩和により目的関数に組み込み, さらに変数
を含む制約条件をラグランジュ緩和により目的関数に組み込み, さらに変数 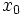 を一時的に固定すると, 問題 (2) に類似した
を一時的に固定すると, 問題 (2) に類似した 個の独立な部分問題に分解される.とくにすべての関数が線形ならば,問題 (3) は部分問題の解を用いて効率的に解けることが知られており,ダンツィク・ウルフ分解法 (Dantzig-Wolfe decomposition method) と呼ばれている.
個の独立な部分問題に分解される.とくにすべての関数が線形ならば,問題 (3) は部分問題の解を用いて効率的に解けることが知られており,ダンツィク・ウルフ分解法 (Dantzig-Wolfe decomposition method) と呼ばれている.
一方,大規模で複雑な問題から取り扱いやすい構造をもつ部分のみを抽出して部分問題を構成し,これを逐次解くことによりもとの問題の解を得ようとする方法は,分割法 (splitting method) と呼ばれている.分割法は,問題 (1) や (3) のようなブロック構造をもたない問題にも適用可能である.また,並列処理可能な部分問題を構成すれば,それらはしばしば小規模な(粒度の細かい)問題となり,SIMD (single instruction stream multiple data stream) 型の大規模並列計算機を用いて効率的に実行できる.
分割法は,線形方程式に対する反復法として,線形代数の分野において古くから研究されている.行列 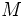 とベクトル
とベクトル  により定義される線形方程式
により定義される線形方程式
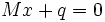
|
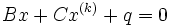
|
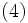 |
の解を 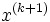 とおくことにより点列
とおくことにより点列 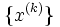 を生成する方法は,行列分割法 (matrix splitting method) と呼ばれる.行列
を生成する方法は,行列分割法 (matrix splitting method) と呼ばれる.行列 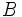 を (ブロック) 対角行列に選べば方程式 (4) は並列的に解けるので,大規模問題に対する効率的な解法を得る.行列分割法は,線形相補性問題や線形変分不等式問題にも拡張できる.
を (ブロック) 対角行列に選べば方程式 (4) は並列的に解けるので,大規模問題に対する効率的な解法を得る.行列分割法は,線形相補性問題や線形変分不等式問題にも拡張できる.
一般の凸計画問題に対しても,分割法に基づくアルゴリズムを構成できる.凸計画問題は,最適性条件を考慮すると,ある写像 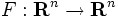 を用いて
を用いて

|
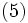 |

|
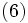 |
の解を 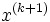 とする反復法は,作用素分割法 (operator splitting method) と呼ばれる.写像
とする反復法は,作用素分割法 (operator splitting method) と呼ばれる.写像  が分離可能ならば部分問題 (6) は並列的に解けるので,大規模な凸計画問題に対する効率的な解法が得られる.
が分離可能ならば部分問題 (6) は並列的に解けるので,大規模な凸計画問題に対する効率的な解法が得られる.
問題 (5) に対する有力な反復法に,近接点法 (proximal point method) がある.近接点法では,単調非減少な正定数の列 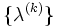 を定め,問題
を定め,問題
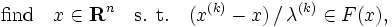
|
の解を 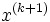 とおく.作用素分割法や近接点法は,一般的な最適化問題のクラスである変分不等式問題にも拡張できる.また,これらの方法を組合せることによりさまざまな並列アルゴリズム(parallel algorithm (nonlinear programming)) を構成できることが知られている.このような考え方に基づく並列アルゴリズムについては,参考文献 [1, 2, 4] に詳しい解説がある.
とおく.作用素分割法や近接点法は,一般的な最適化問題のクラスである変分不等式問題にも拡張できる.また,これらの方法を組合せることによりさまざまな並列アルゴリズム(parallel algorithm (nonlinear programming)) を構成できることが知られている.このような考え方に基づく並列アルゴリズムについては,参考文献 [1, 2, 4] に詳しい解説がある.
[1] D. P. Bertsekas and J. N. Tsitsiklis, Parallel and Distributed Computation: Numerical Methods, Prentice-Hall, 1989.
[2] Y. Censor and S. A. Zenios, Parallel Optimization: Theory, Algorithms, and Applications, Oxford University Press, 1997.
[3] J. F. Shapiro, Mathematical Programming: Structures and Algorithms, John Wiley & Sons, 1979.
- 大規模問題の分解法のページへのリンク
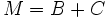 を
を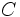 を
を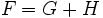 を
を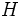 を
を