ほうぶつ‐せん〔ハウブツ‐〕【放物線/×抛物線】
放物線
放物線
放物線
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/01/29 10:22 UTC 版)


放物線(ほうぶつせん、拋物線・抛物線、希:παραβολή「parabolē」、羅、英: parabola、独: Parabel)[1]とは、その名の通り地表(つまり重力下)で投射した物体の運動(放物運動)が描く軌跡のことである。 放物線をその対称軸を中心として回転させた曲面を放物面という。
数学的定義
放物線は、円錐曲線の一つである。数学的な定義としてよく知られたものはいくつかの方法があるが、いずれも適当な枠組みで互いに他を導出することができる等価なものである。
軌跡

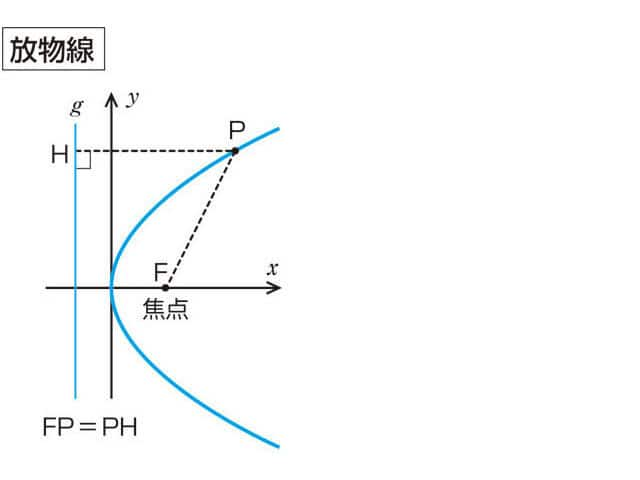
平面幾何学において放物線(ほうぶつせん、parabola)とは、準線 (directrix) と呼ばれる直線 L と、その上にない焦点 (focus) と呼ばれる一点 F が与えられるとき、準線 L と焦点 F とをともに含む唯一つの平面 π 上の点 P であって、P から焦点 F への距離 PF と等しい距離 PQ を持つような準線 L 上の点 Q が存在するようなものの軌跡として定義される平面曲線である。
放物線上の点を P(x, y)、焦点を F(0, a)、準線の式を y = −a とすると PQ = PF より
円錐面の平面 π による断面(赤い面の縁)が、準線 L と焦点 F をもつ放物線を描くことが確認できる 二次曲線

y = x2 と x = y2 (y > 0) - 焦点が (0, c)、準線が y = −c のとき、放物線の式 x2 = 4cy となる。
- 焦点が (c, 0)、準線が x = −c のとき、放物線の式は y2 = 4cx となる。
- 二次関数 y = ax2 + bx + c (a は 0 ではない)が描くグラフは放物線になる。
作図

準線 l と焦点 F の定める放物線の作図法 焦点と準線による定義から実際に放物線を糸や三角定規などを用いて作図することができる。
- 放物線の焦点 F と準線 l をとる
- 三角定規の直角を挟む一辺の長さ |AB| に合わせた糸を用意する(右図参照)
- 糸の両端を点 A と焦点 F に固定する
- 三角定規の直角を挟む残りの一辺が準線に沿ってを滑るにようにする(たとえば準線に定規をおいて合わせる)
- 鉛筆で糸を辺 AB 上の点 P に押し当て、糸を張る
- 三角定規を準線に沿って滑らすと、鉛筆は放物線を描く(軌跡は |PF| = |PB| ゆえ放物線になる)
物理学的な導出

初速 v, 角度 θ で初期の高さ y0 から投げ出した物体の描く曲線 質量 m の物体を斜めに投射するとき、投げ出されたあとの物体に掛かる力は、空気抵抗の存在しない理想的な状況下では下向きに掛かる重力 mg のみ(g は重力加速度)である。したがって、運動方程式 F = ma から、物体の加速度は

準線(緑)と焦点(青丸)は同じ長さの線(青)を半径と思うと、放物線上の点を中心とする同じ円(水色の破線)の上にある。放物線に無限遠から来る、準線への直交射影となる光線は、放物線と直交する直線(赤)を軸として対称に反射して焦点を結ぶ。 - 焦点から準線に引いた垂線は、この放物線の唯一の対称軸になる。放物線とその対称軸との交点を、この放物線の頂点と呼ぶ。放物線をその対称軸の周りに回転させてできる曲面を回転放物面、または単に放物面 (paraboloid) と呼ぶ。

放物面鏡による平行光線の反射。 
エッフェル塔の下部アーチ。 包絡線

準線上の点から放物線に引いた二本の接線 直線LとL上にない1点Fを固定し、L上に任意の点Pをとると、 直線PFと直線Lのなす角の2等分線は、直線Lを準線、点Fを焦点とする放物線の包絡線となる。
これを利用して、紙の折り跡から放物線を浮かび上がらせることができる[2]。

ナイルズの放物線  この節の加筆が望まれています。
この節の加筆が望まれています。微積分

原点での曲率円  この節の加筆が望まれています。
この節の加筆が望まれています。電子
二次近似
詳細は「テイラーの定理」を参照ある曲線 γ が(γ 上の)ある点 P において C2-級ならば、γ は P の十分近くである放物線(の一部)にほぼ一致する。γ が必ずしも一定の平面上にある曲線ではないとしても、P において C2-級という条件から、P の十分近くであれば一定の平面上にほぼ乗っていると考えられる。別な言い方をすれば、任意の C2-級曲線は各点で放物線と二次の接触を持つ。
- これは、C1-級曲線が各点の近傍で接線と呼ばれる直線(線分)で近似されることの類似である。

シンプソンの近似 関数のグラフを放物線によって近似し、その関数の積分を計算する数値積分法にシンプソンの方法がある。このときの近似誤差はテイラーの式の3次の剰余項を適当に評価することで測れる。被積分関数が3次までの多項式関数ならば、シンプソンの公式による数値積分は誤差無しに積分値を得ることができる。
カテナリー曲線

カテナリー曲線(緑線)と放物線(赤線)の比較 カテナリー曲線(懸垂線)は、見た目が放物線と似ていて混同されることがあるが、全く別物である。共通した性質として、
- 唯一の極小な頂点を持つ
- 下に凸な滑らかな曲線
- 頂点を通る直線を対称の軸として線対称
があり、両者は頂点付近の十分近くで微視的にはほぼ一致するが、巨視的にはかけ離れた形状を示す。
参考文献
- 『曲線の事典 性質・歴史・作図法』 礒田正美、Maria G. Bartolini Bussi編、田端毅、讃岐勝、礒田正美著:共立出版、2009年 ISBN 9784320019072
脚注
- ^ 当用漢字制定以前は「拋物線又は抛物線(抛は拋の異体字)」の表記が多かったが、「拋・抛」が当用漢字表外であった為、1956年(昭和31年)に国語審議会が発表した指針「同音の漢字による書きかえ」により現在では「放」が一般に使用されている。
- ^ 折り紙による2次曲線
関連項目
外部リンク
- Köller, Jürgen, "Parabeln" - Mathematische Basteleien. (ドイツ語)
- Weisstein, Eric W. "Parabola". mathworld.wolfram.com (英語).
- スコーテンの放物線作図器
- 「みんなここに集まってくる」 ― 大科学実験
放物線
「放物線」の例文・使い方・用例・文例
- 放物線のページへのリンク