シージー‐ほう〔‐ハフ〕【CG法】
読み方:しーじーほう
《conjugate gradient method》⇒共役勾配法
共役勾配法
共役勾配法
(conjugate gradient method から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/06/11 14:11 UTC 版)

共役勾配法(きょうやくこうばいほう、英: conjugate gradient method、CG法とも呼ばれる)は対称正定値行列を係数とする連立一次方程式を解くためのアルゴリズムである[1][2][3][4]。反復法として利用され[1][2][3][4]、コレスキー分解のような直接法では大きすぎて取り扱えない、大規模な疎行列を解くために利用される。そのような問題は偏微分方程式などを数値的に解く際に常に現れる[1][5][6][7]。
共役勾配法は、エネルギー最小化などの最適化問題を解くために用いることもできる[8][9][10]。
双共役勾配法は、共役勾配法の非対称問題への拡張である[11]。
また、非線形問題を解くために、さまざまな非線形共役勾配法が提案されている[12][13][14][15]。
詳説
対称正定値行列Aを係数とするn元連立一次方程式
Ax = b
の解をx*とする。
直接法としての共役勾配法
非零ベクトルu、vが
「conjugate gradient method」の例文・使い方・用例・文例
- conjugate gradient methodのページへのリンク
 次
次
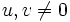 が
が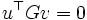 を
を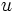 と
と  は
は 


