ボロノイ図
【英】:Voronoi diagram
概要
空間に, 互いに共通部分をもたない有限個の図形を配置すると, それぞれの図形のまわりには他の図形より自分に近い点からなる領域が定まる. この領域をその図形のボロノイ領域という. 空間のボロノイ領域への分割をボロノイ図といい, はじめに配置された図形をこのボロノイ図の生成元という. 生成元, 距離, 空間の次元の選び方によってボロノイ図には多くの種類がある. ボロノイ図は, 勢力圏を表すものと解釈でき, 地理的最適化などに応用されている.
詳説
空間に生成元とよばれるいくつかの図形が配置されているとき, 空間の各点を最も近い生成元へ割り当てた構造をボロノイ図 (Voronoi diagram) という. 一つの生成元に割り当てられた点全体がなす領域を, その生成元のボロノイ領域または勢力圏という.
空間 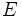 に配置された生成元を
に配置された生成元を 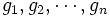 とし, 生成元の集合を
とし, 生成元の集合を  とする. 任意の点
とする. 任意の点 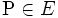 から
から 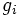 までの距離を
までの距離を 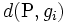 で表す.
で表す. 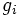 のボロノイ領域
のボロノイ領域 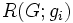 は
は
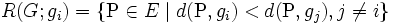
と表すことができる. 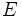 は,
は, 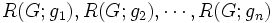 とそれらの境界に分割されるが, その分割構造がボロノイ図である. 空間
とそれらの境界に分割されるが, その分割構造がボロノイ図である. 空間 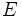 と, 生成元
と, 生成元 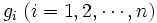 と距離
と距離  の選び方によってさまざまなボロノイ図が定義できる.
の選び方によってさまざまなボロノイ図が定義できる.
点を生成元とし, ユークリッド距離を距離とするボロノイ図は点ボロノイ図 (Voronoi diagram for points) とよばれる. 2次元では, ボロノイ領域の境界は, 両側の生成元を結ぶ線分の垂直二等分線の上にあり, 3つのボロノイ領域の境界が共有する点はまわりの 3 個の生成元を通る円の中心である.
点ボロノイ図に対して, ボロノイ領域が隣り合う生成元を線分で結ぶことによってできる図形はドロネー図 (Delaunay diagram) とよばれる.
互いに交差しない線分を生成元とし, ユークリッド距離を距離とするボロノイ図は線分ボロノイ図 (Voronoi diagram for line segments) よばれる. 2 次元線分ボロノイ図の境界は線分と放物線の一部によって構成される.
中心が 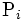 , 半径が
, 半径が 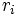 の円を
の円を 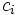 とする. 点
とする. 点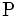 に対して
に対して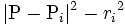 を, 点
を, 点 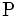 と円
と円 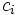 のラゲール (Laguerre) 距離という. ただし
のラゲール (Laguerre) 距離という. ただし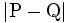 は 2 点
は 2 点 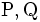 のユークリッド距離を表す. 円
のユークリッド距離を表す. 円 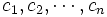 を生成元とし, ラゲール距離を距離とするボロノイ図をラゲールボロノイ図 (Laguere Voronoi diagram) またはパワー図 (power diagram) とよぶ. ラゲールボロノイ図の境界は超平面の一部である. 特に2次元では直線の一部であり, 3次元では平面の一部である.
を生成元とし, ラゲール距離を距離とするボロノイ図をラゲールボロノイ図 (Laguere Voronoi diagram) またはパワー図 (power diagram) とよぶ. ラゲールボロノイ図の境界は超平面の一部である. 特に2次元では直線の一部であり, 3次元では平面の一部である.
このほかにも 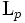 -距離, ハウスドルフ距離などさまざまな距離を用いてボロノイ図が定義できる. このように一般の距離に基づいて定義されるボロノイ図を一般距離ボロノイ図 (Voronoi diagram based on a general distance) とよぶ.
-距離, ハウスドルフ距離などさまざまな距離を用いてボロノイ図が定義できる. このように一般の距離に基づいて定義されるボロノイ図を一般距離ボロノイ図 (Voronoi diagram based on a general distance) とよぶ.
たとえば, 点を生成元とし, ユークリッド距離の逆数を距離とみなして定義されるボロノイ図は最遠点ボロノイ図 (farthest-point Voronoi diagram) とよばれる. このボロノイ図では, 他の生成元より自分の方が離れているという領域がそれぞれの生成元のボロノイ領域となる. 空でないボロノイ領域をもつのは, 生成元の凸包の境界上に現れる生成元のみである.
生成元がその位置や形を時間とともに変えると, 対応するボロノイ図も時間とともに変化する. このように時間の関数となるボロノイ図は動的ボロノイ図 (dynamic Voronoi diagram) とよばれる. 動的ボロノイ図は, 飛行機やロボットが互いに接近し過ぎないよう監視するときなどに役立つ.
平面上に与えられた有限個の点の集合を  とする.
とする.  を含む最小の円を
を含む最小の円を の最小包含円 (minimum enclosing circle) という.
の最小包含円 (minimum enclosing circle) という.  の最小包含円は,
の最小包含円は,  のちょうど 2 個の点を境界上にもつか, 3個以上の点を境界上にもつかのいずれかである. 前者の場合の最小包含円の中心は
のちょうど 2 個の点を境界上にもつか, 3個以上の点を境界上にもつかのいずれかである. 前者の場合の最小包含円の中心は を生成元集合とする最遠点ボロノイ図の辺上にあり, 後者の場合の最小包含円の中心はその最遠点ボロノイ図の頂点のいずれかと一致する.
を生成元集合とする最遠点ボロノイ図の辺上にあり, 後者の場合の最小包含円の中心はその最遠点ボロノイ図の頂点のいずれかと一致する.
平面上の一つの多角形を 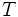 とし,
とし, 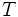 内に指定された有限個の点の集合を
内に指定された有限個の点の集合を  とする.
とする. 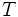 内に中心をもち,
内に中心をもち,  の要素を一つも内部に含まない円を空円といい, その中で半径が最大のものを最大空円 (maximum empty circle) という. 最大空円の中心は,
の要素を一つも内部に含まない円を空円といい, その中で半径が最大のものを最大空円 (maximum empty circle) という. 最大空円の中心は, 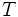 の頂点か,
の頂点か,  を生成元集合とするボロノイ図の頂点か, あるいはボロノイ図の辺と
を生成元集合とするボロノイ図の頂点か, あるいはボロノイ図の辺と 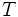 の境界辺の交点のいずれかである.
の境界辺の交点のいずれかである.
ボロノイ図の効率のよい構成法はたくさん知られている. たとえば 2次元では, 点ボロノイ図, 線分ボロノイ図, ラゲールボロノイ図が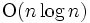 の計算量で構成できる.
の計算量で構成できる.  次元空間 (
次元空間 (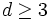 ) における点ボロノイ図とラゲールボロノイ図は,
) における点ボロノイ図とラゲールボロノイ図は, 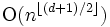 の計算量で構成できる. ただし
の計算量で構成できる. ただし 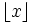 は
は  以下の最大の整数である.
以下の最大の整数である.
ボロノイ図に関する詳しい解説には [1, 2, 3] がある.
[1] F. Aurenhammer, "Voronoi Diagrams -A Survey of a Fundamental Geometric Data Structure," ACM Computing Surveys, 23 (1991), 345-405.
[2] A. Okabe, B. Boots, K. Sugihara and S.-N. Chiu, Spatial Tessellations -Concepts and Applications of Voronoi Diagrams, 2nd Edition, John Wiley and Sons, Inc., Chichester, 2000.
[3] S. Fortune, "Voronoi Diagrams and Delaunay Triangulations," in Computing in Euclidean Geometry, 2nd Edition, D. -Z. Du and F. Hwang, eds., World Scientific, Singapore, 225-265, 1995.
- Voronoi Diagramのページへのリンク
